Có \(6\) chiếc ghế được kê thành một hàng ngang, xếp ngẫu nhiên \(6\) học sinh, gồm \(3\) học sinh lớp A, \(2\) học sinh lớp B và \(1\) học sinh lớp C, ngồi vào hàng ghế đó, sao cho mỗi ghế có đúng \(1\) học sinh. Xác suất để học sinh lớp C chỉ ngồi cạnh học sinh lớp B bằng

	\(\dfrac{1}{6}\)
	\(\dfrac{3}{20}\)
	\(\dfrac{2}{15}\)
	\(\dfrac{1}{5}\)

Trong không gian \(Oxyz\), cho hai điểm \(M\left(1;0;1\right)\) và \(N\left(3;2;-1\right)\). Đường thẳng \(MN\) có phương trình tham số là

	\(\begin{cases}x=1+2t\\ y=2t\\ z=1+t\end{cases}\)
	\(\begin{cases}x=1+t \\ y=t \\ z=1+t\end{cases}\)
	\(\begin{cases}x=1-t \\ y=t \\ z=1+t\end{cases}\)
	\(\begin{cases}x=1+t \\ y=t \\ z=1-t\end{cases}\)

Trong không gian \(Oxyz\), cho điểm \(M\left(2;1;0\right)\) và đường thẳng \(\Delta\colon\dfrac{x-3}{1}=\dfrac{y-1}{4}=\dfrac{z+1}{-2}\). Mặt phẳng đi qua \(M\) và vuông góc với \(\Delta\) có phương trình là

	\(3x+y-z-7=0\)
	\(x+4y-2z+6=0\)
	\(x+4y-2z-6=0\)
	\(3x+y-z+7=0\)

Gọi \(z_0\) là nghiệm phức có phần ảo âm của phương trình \(z^2-2z+5=0\). Môđun của số phức \(z_0+i\) bằng

	\(2\)
	\(\sqrt{2}\)
	\(\sqrt{10}\)
	\(10\)

Cho hai số phức \(z_1=3-i\), \(z_2=-1+i\). Phần ảo của số phức \(z_1z_2\) bằng

	\(4\)
	\(4i\)
	\(-1\)
	\(-i\)

Diện tích \(S\) của hình phẳng giới hạn bởi các đường \(y=2x^2\), \(y=-1,\,x=0\) và \(x=1\) được tính bởi công thức nào dưới đây?

	\(S=\pi\displaystyle\int\limits_0^1\left(2x^2+1\right)\mathrm{\,d}x\)
	\(S=\displaystyle\int\limits_0^1\left(2x^2-1\right)\mathrm{\,d}x\)
	\(S=\displaystyle\int\limits_0^1\left(2x^2+1\right)^2\mathrm{\,d}x\)
	\(S=\displaystyle\int\limits_0^1\left(2x^2+1\right)\mathrm{\,d}x\)

Xét \(\displaystyle\int\limits_0^2x\cdot\mathrm{e}^{x^2}\mathrm{\,d}x\), nếu đặt \(u=x^2\) thì \(\displaystyle\int\limits_0^2x\cdot\mathrm{e}^{x^2}\mathrm{\,d}x\) bằng

	\(2\displaystyle\int\limits_0^2\mathrm{e}^u\mathrm{\,d}u\)
	\(2\displaystyle\int\limits_0^4\mathrm{e}^u\mathrm{\,d}u\)
	\(\dfrac{1}{2}\displaystyle\int\limits_0^2\mathrm{e}^u\mathrm{\,d}u\)
	\(\dfrac{1}{2}\displaystyle\int\limits_0^4\mathrm{e}^u\mathrm{\,d}u\)

Trong không gian, cho tam giác \(ABC\) vuông tại \(A\), \(AB=a\) và \(AC=2a\). Khi quay tam giác \(ABC\) quanh cạnh góc vuông \(AB\) thì đường gấp khúc \(ACB\) tạo thành một hình nón. Diện tích xung quanh của hình nón đó bằng

	\(5\pi a^2\)
	\(\sqrt{5}\pi a^2\)
	\(2\sqrt{5}\pi a^2\)
	\(10\pi a^2\)

Tập nghiệm của bất phương trình \(9^x+2\cdot3^x-3>0\) là

	\(\left[0;+\infty\right)\)
	\(\left(0;+\infty\right)\)
	\(\left(1;+\infty\right)\)
	\(\left[1;+\infty\right)\)

Số giao điểm của đồ thị hàm số \(y=x^3-3x+1\) và trục hoành là

	\(3\)
	\(0\)
	\(2\)
	\(1\)

Xét các số thực \(a,\,b\) thỏa mãn \(\log_3\left(3^a\cdot9^b\right)=\log_93\). Mệnh đề nào là đúng?

	\(a+2b=2\)
	\(4a+2b=1\)
	\(4ab=1\)
	\(2a+4b=1\)

Giá trị nhỏ nhất của hàm số \(y=x^4-10x^2+2\) trên đoạn \(\left[-1;2\right]\) bằng

	\(2\)
	\(-23\)
	\(-22\)
	\(-7\)

Cho hàm số \(f\left(x\right)\) có bảng xét dấu của \(f'\left(x\right)\) như sau:

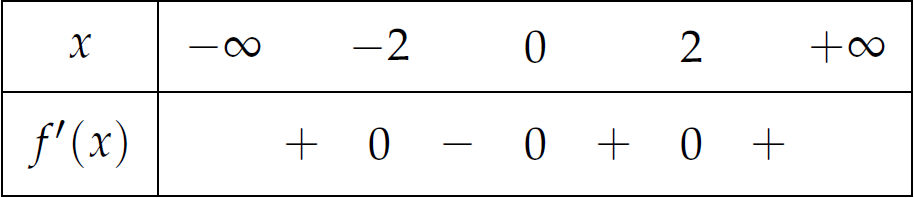
Số điểm cực trị của hàm số đã cho là

	\(3\)
	\(0\)
	\(2\)
	\(1\)

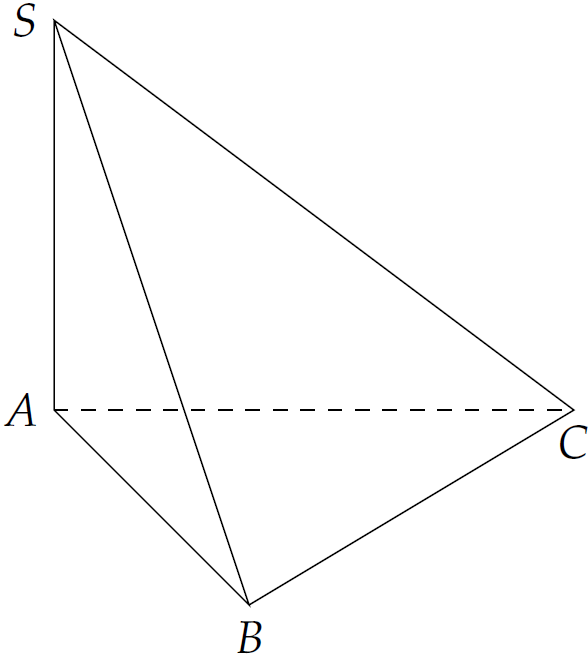
Cho hình chóp \(S.ABC\) có \(SA\) vuông góc với mặt phẳng \(\left(ABC\right)\), \(SA=a\sqrt{2}\), tam giác \(ABC\) vuông cân tại \(B\) và \(AC=2a\) (minh họa như hình trên). Góc giữa đường thẳng \(SB\) và mặt phẳng \(\left(ABC\right)\) bằng

	\(30^\circ\)
	\(45^\circ\)
	\(60^\circ\)
	\(90^\circ\)

Trong không gian \(Oxyz\), cho đường thẳng \(d\colon\dfrac{x-1}{2}=\dfrac{y-2}{3}=\dfrac{z+1}{-1}\). Điểm nào dưới đây thuộc \(d\)?

	\(P\left(1;2;-1\right)\)
	\(M\left(-1;-2;1\right)\)
	\(N\left(2;3;-1\right)\)
	\(Q\left(-2;-3;1\right)\)

Trong không gian \(Oxyz\), cho mặt phẳng \(\left(P\right)\colon2x+3y+z+2=0\). Vectơ nào dưới đây là một vectơ pháp tuyến của \(\left(P\right)\)?

	\(\overrightarrow{n_3}=\left(2;3;2\right)\)
	\(\overrightarrow{n_1}=\left(2;3;0\right)\)
	\(\overrightarrow{n_2}=\left(2;3;1\right)\)
	\(\overrightarrow{n_4}=\left(2;0;3\right)\)

Trong không gian \(Oxyz\), cho mặt cầu \(\left(S\right)\colon\left(x-2\right)^2+\left(y+4\right)^2+\left(z-1\right)^2=9\). Tâm của \(\left(S\right)\) có tọa độ là

	\(\left(-2;4;-1\right)\)
	\(\left(2;-4;1\right)\)
	\(\left(2;4;1\right)\)
	\(\left(-2;-4;-1\right)\)

Trong không gian \(Oxyz\), hình chiếu vuông góc của điểm \(M\left(2;1;-1\right)\) trên mặt phẳng \(\left(Ozx\right)\) có tọa độ là

	\(\left(0;1;0\right)\)
	\(\left(2;1;0\right)\)
	\(\left(0;1;-1\right)\)
	\(\left(2;0;-1\right)\)

Trên mặt phẳng tọa độ, điểm biểu diễn số phức \(z=-1+2i\) là điểm nào dưới đây?

	\(Q\left(1;2\right)\)
	\(P\left(-1;2\right)\)
	\(N\left(1;-2\right)\)
	\(M\left(-1;-2\right)\)

Cho hai số phức \(z_1=2+i\) và \(z_2=1+3i\). Phần thực của số phức \(z_1+z_2\) bằng

	\(1\)
	\(3\)
	\(4\)
	\(-2\)