Bất phương trình nào dưới đây là bất phương trình bậc nhất hai ẩn?

	\(2x-5y+3z\leq0\)
	\(3x^2+2x-4>0\)
	\(2x^2+5y>3\)
	\(2x+3y<5\)

Tập nghiệm của bất phương trình \(\left|2x-1\right|\leq1\) là

	\(S=(0;1)\)
	\(S=\{0;1\}\)
	\(S=[0;1]\)
	\(S=(-\infty;0]\cup[1;+\infty)\)

Tập nghiệm của bất phương trình \(\left|2x^2-5x+3\right|+\left|x^2-1\right|\leq0\) là

	\(\left[\dfrac{2}{3};4\right]\)
	\(\left[\dfrac{2}{3};4\right]\setminus\{1\}\)
	\(\varnothing\)
	\(\{1\}\)

Với giá trị nào của \(x\) thì biểu thức \(f(x)=\left|2x-5\right|-3\) không dương?

	\(x<1\)
	\(x=\dfrac{5}{2}\)
	\(x=0\)
	\(1\leq x\leq4\)

Bất phương trình \(\left|x-5\right|\leq4\) có bao nhiêu nghiệm nguyên?

	\(10\)
	\(8\)
	\(9\)
	\(7\)

Cho \(a\) là số thực dương. Mệnh đề nào dưới đây đúng?

	\(|x|\geq a\Leftrightarrow-a\leq x\leq a\)
	\(|x|\leq a\Leftrightarrow x\leq a\)
	\(|x|>a\Leftrightarrow x>a\)
	\(|x|\geq a\Leftrightarrow\left[\begin{array}{l}x\geq a\\ x\leq-a\end{array}\right.\)

Để phương trình \(\left(m^2-4\right)x^2+5x+m=0\) có hai nghiệm trái dấu thì

	\(m\in(\infty;-2]\cup[0;2]\)
	\(m\in(-\infty;-2)\cup(0;2)\)
	\(m\in(-2;0)\cup(2;+\infty)\)
	\(m\in(-2;2)\)

Tập nghiệm của bất phương trình \((x+2)(5-x)<0\) là

	\([5;+\infty)\)
	\((-\infty;-2)\cup(5;+\infty)\)
	\((-2;5)\)
	\((-5;-2)\)

Số nghiệm nguyên dương của bất phương trình \((2-x)(x+1)(3-x)\leq0\) là

	\(1\)
	\(4\)
	\(2\)
	\(3\)

Tập nghiệm của bất phương trình \(\dfrac{1}{x-1}\geq\dfrac{1}{x+1}\) là

	\((-1;1)\)
	\((-\infty;-1)\cup(1;+\infty)\)
	\((-\infty;-1]\cup[1;+\infty)\)
	\((-\infty;-1)\)

Với \(x\) thuộc tập hợp nào dưới đây thì biểu thức \(f(x)=\dfrac{2-x}{2x+1}\) không âm?

	\(\left(-\dfrac{1}{2};2\right)\)
	\(\left(-\dfrac{1}{2};2\right]\)
	\(\left(-\infty;-\dfrac{1}{2}\right)\cup\left(2;+\infty\right)\)
	\(\left(-\infty;-\dfrac{1}{2}\right)\cup[2;+\infty)\)

Cho \(f(x)=2x+1\). Khẳng định nào sau đây sai?

	\(f(x)>0,\,\forall x>-\dfrac{1}{2}\)
	\(f(x)>0,\,\forall x<\dfrac{1}{2}\)
	\(f(x)>0,\,\forall x>2\)
	\(f(x)>0,\,\forall x>0\)

Bảng xét dấu sau là của biểu thức nào?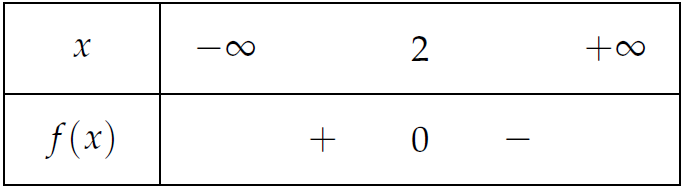

	\(f(x)=x-2\)
	\(f(x)=2-4x\)
	\(f(x)=16-8x\)
	\(f(x)=-x-2\)

Nhị thức \(f(x)=2x-6\) dương trên

	\((3;+\infty)\)
	\((-\infty;3)\)
	\([3;+\infty)\)
	\((-\infty;3]\)

Nhị thức \(-2x-3\) nhận giá trị dương khi và chỉ khi

	\(x<-\dfrac{3}{2}\)
	\(x\leq-\dfrac{2}{3}\)
	\(x>-\dfrac{3}{2}\)
	\(x\geq-\dfrac{2}{3}\)

Tìm nghiệm của nhị thức \(f(x)=3x+6\).

	\(x=2\)
	\(x=-2\)
	\(x=-3\)
	\(x=3\)

Tổng tất cả các nghiệm nguyên của hệ bất phương trình \(\begin{cases}
5x-2<4x+5\\
x^2<(x+2)^2
\end{cases}\) bằng

	\(21\)
	\(28\)
	\(27\)
	\(29\)

Số nghiệm nguyên của hệ bất phương trình \(\begin{cases}
6x+\dfrac{5}{7}<4x+7\\
\dfrac{8x+3}{2}<2x+25
\end{cases}\) là

	\(8\)
	\(9\)
	\(10\)
	Vô số

Tập nghiệm của hệ bất phương trình \(\begin{cases}\dfrac{2x-1}{3}<-x+1\\ \dfrac{4-3x}{2}<3-x\end{cases}\) là

	\(\left(-2;\dfrac{4}{5}\right)\)
	\(\left[-2;\dfrac{4}{5}\right]\)
	\(\left(-2;\dfrac{3}{5}\right)\)
	\(\left[-1;\dfrac{1}{3}\right)\)

Tập nghiệm của hệ bất phương trình \(\begin{cases}\dfrac{4x+5}{6}<x-3\\ 2x+3>\dfrac{7x-4}{3}\end{cases}\) là

	\(\left(\dfrac{23}{2};13\right)\)
	\((-\infty;13)\)
	\((13;+\infty)\)
	\(\left(-\infty;\dfrac{23}{2}\right)\)