Cho hai hàm số \(y=f(x)\) và \(y=g(x)\) lên tục trên đoạn \([a;b]\). Gọi \(D\) là hình phẳng giới hạn bởi đồ thị hai hàm số và hai đường thẳng \(x=a\), \(x=b\) (\(a< b\)). Diện tích của \(D\) được tính theo công thức
| \(S=\displaystyle\int\limits_{a}^{b}\left|f(x)-g(x)\right|\mathrm{\,d}x\) | |
| \(S=\displaystyle\int\limits_{b}^{a}\left|f(x)-g(x)\right|\mathrm{\,d}x\) | |
| \(S=\pi\displaystyle\int\limits_{a}^{b}\left|f(x)-g(x)\right|\mathrm{\,d}x\) | |
| \(S=\left|\displaystyle\int\limits_{a}^{b}\left[f(x)-g(x)\right]\mathrm{\,d}x\right|\) |
Cho hàm số \(y=f(x)\) liên tục trên \([a;b]\). Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y=f(x)\), trục hoành và hai đường thẳng \(x=a\), \(x=b\) được xác định bởi công thức
| \(S=\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x\) | |
| \(S=\displaystyle\int\limits_{b}^{a}\left|f(x)\right|\mathrm{\,d}x\) | |
| \(S=\displaystyle\int\limits_{a}^{b}\left|f(x)\right|\mathrm{\,d}x\) | |
| \(S=-\displaystyle\int\limits_{b}^{a}f(x)\mathrm{\,d}x\) |
Cho hàm số \(y=f(x)\) liên tục trên \([a;b]\). Gọi \(D\) là hình phẳng giới hạn bởi đồ thị hàm số \(y=f(x)\), trục hoành và hai đường thẳng \(x=a\), \(x=b\) (\(a<b\)). Diện tích hình phẳng \(D\) được xác định bởi công thức
| \(S=\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x\) | |
| \(S=\displaystyle\int\limits_{a}^{b}\left|f(x)\right|\mathrm{\,d}x\) | |
| \(S=\pi\displaystyle\int\limits_{a}^{b}f^2(x)\mathrm{\,d}x\) | |
| \(S=\displaystyle\int\limits_{a}^{b}f^2(x)\mathrm{\,d}x\) |
Trong không gian \(Oxyz\), mặt phẳng \((P)\) cắt trục \(Oz\) tại điểm có cao độ bằng \(2\) và song song với mặt phẳng \((Oxy)\). Phương trình mặt phẳng \((P)\) là
| \(z-2=0\) | |
| \(x-2=0\) | |
| \(y+z-2=0\) | |
| \(x-y-2=0\) |
Trong không gian \(Oxyz\), cho điểm \(A(4;-3;2)\). Hình chiếu vuông góc của \(A\) lên các trục tọa độ \(Ox,\,Oy,\,Oz\) lần lượt là \(M,\,N,\,P\). Phương trình mặt phẳng \((MNP)\) là
| \(4x-3y+2z-5=0\) | |
| \(3x-4y+6z-12=0\) | |
| \(2x-3y+4z-1=0\) | |
| \(\dfrac{x}{4}-\dfrac{y}{3}+\dfrac{z}{2}+1=0\) |
Trong không gian \(Oxyz\), mặt phẳng \((\alpha)\) cắt ba trục tọa độ lần lượt tại các điểm \(M(8;0;0)\), \(N(0;-2;0)\) và \(P(0;0;4)\). Phương trình mặt phẳng \((\alpha)\) là
| \(\dfrac{x}{8}+\dfrac{y}{-2}+\dfrac{z}{4}=0\) | |
| \(\dfrac{x}{4}+\dfrac{y}{-1}+\dfrac{z}{2}=1\) | |
| \(x-4y+2z=0\) | |
| \(x-4y+2z-8=0\) |
Trong không gian \(Oxyz\), cho hai điểm \(M(2;0;-1)\), \(N(1;-1;3)\) và mặt phẳng \((P)\colon3x+2y-z+5=0\). Gọi \((\alpha)\) là mặt phẳng đi qua \(M,\,N\) và vuông góc với \((P)\). Phương trình mặt phẳng \((\alpha)\) là
| \(-7x+11y+z-3=0\) | |
| \(7x-11y+z-1=0\) | |
| \(-7x+11y+z+15=0\) | |
| \(7x-11y-z+1=0\) |
Trong không gian \(Oxyz\), mặt phẳng \((\alpha)\) đi qua \(A(2;-1;1)\) và vuông góc với hai mặt phẳng \((P)\colon2x-z+1=0\) và \((Q)\colon y=0\). Phương trình mặt phẳng \((\alpha)\) là
| \(2x+y-4=0\) | |
| \(x+2z-4=0\) | |
| \(x+2y+z=0\) | |
| \(2x-y+z=0\) |
Trong không gian \(Oxyz\), mặt phẳng \((\alpha)\) đi qua điểm \(M(0;0;-1)\) và song song với giá của hai vectơ \(\vec{a}=(1;-2;3)\), \(\vec{b}=(3;0;5)\). Phương trình của \((\alpha)\) là
| \(-5x+2y+3z+3=0\) | |
| \(5x-2y-3z-21=0\) | |
| \(10x-4y-6z+21=0\) | |
| \(5x-2y-3z+21=0\) |
Trong không gian \(Oxyz\), cho hai điểm \(M(1;-1;5)\) và \(N(0;0;1)\). Mặt phẳng \((\alpha)\) chứa \(M,\,N\) và song song với trục \(Oy\) có phương trình là
| \(4x-z+1=0\) | |
| \(x-4z+2=0\) | |
| \(2x+z-3=0\) | |
| \(x+4z-1=0\) |
Trong không gian \(Oxyz\), cho ba điểm \(A(3;-1;2)\), \(B(4;-1;-1)\) và \(C(2;0;2)\). Mặt phẳng đi qua ba điểm \(A,\,B,\,C\) có phương trình là
| \(3x-3y+z-14=0\) | |
| \(3x+3y+z-8=0\) | |
| \(3x-2y+z-8=0\) | |
| \(2x+3y-z+8=0\) |
Một vườn hoa có dạng hình tròn, bán kính bằng \(5\) m. Phần đất trồng hoa là phần tô trong hình vẽ.
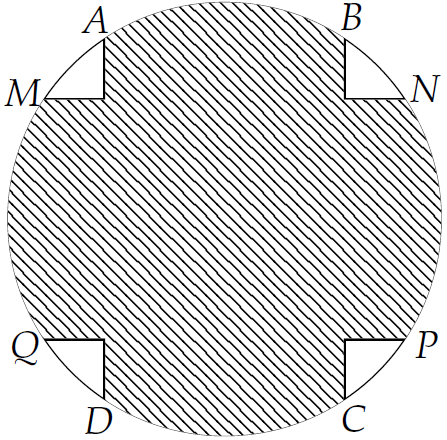
Kinh phí để trồng hoa là \(50.000\) đồng/m\(^2\). Hỏi số tiền (làm tròn đến hàng đơn vị) cần để trồng hoa trên diện tích phần đất đó là bao nhiêu? Biết hai hình chữ nhật \(ABCD\) và \(MNPQ\) có \(AB=MQ=5\) m.
| \(3.533.057\) đồng | |
| \(3.641.528\) đồng | |
| \(3.641.529\) đồng | |
| \(3.533.058\) đồng |
Ba Tí muốn làm cửa sắt được thiết kế như hình.
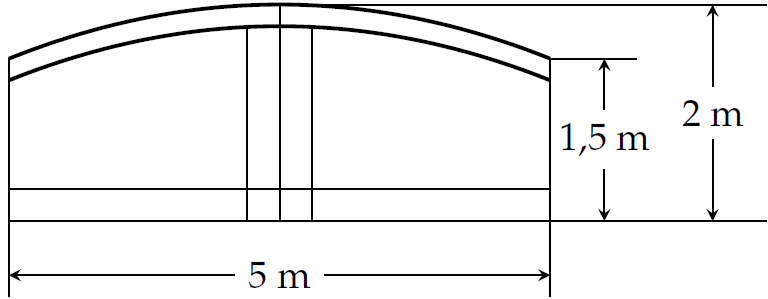
Vòm cổng có hình dạng một parabol. Giá \(1\)m\(^2\) cửa sắt là \(660000\) đồng. Cửa sắt có giá (nghìn đồng) là
| \(6500\) | |
| \(\dfrac{55}{6}\cdot10^3\) | |
| \(5600\) | |
| \(6050\) |
Trên bức tường cần trang trí một hình phẳng dạng parabol đỉnh \(S\) như hình vẽ, biết \(OS=AB=4\) cm, \(O\) là trung điểm \(AB\).
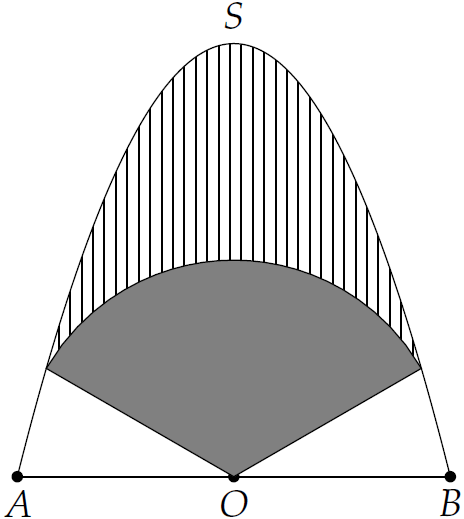
Parabol trên được chia thành ba phần để sơn ba màu khác nhau với mức chi phí: phần trên là phần kẻ sọc \(140000\) đồng/m\(^2\), phần giữa là hình quạt tâm \(O\), bán kính \(2\) m được tô đậm \(150000\) đồng/m\(^2\), phần còn lại \(160000\) đồng/m\(^2\). Tổng chi phí để sơn cả ba phần gần nhất với số nào sau đây?
| \(1.597.000\) đồng | |
| \(1.625.000\) đồng | |
| \(1.575.000\) đồng | |
| \(1.600.000\) đồng |
Một quán cà phê muốn làm cái bảng hiệu là một phần của Elip có kích thước, hình dạng giống như hình vẽ và có chất lượng bằng gỗ.
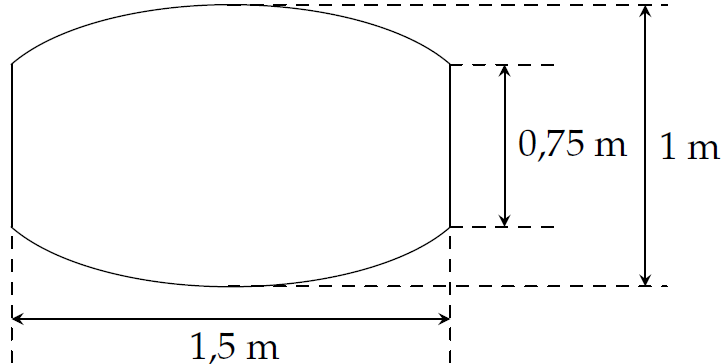
Diện tích gỗ bề mặt bẳng hiệu làm tròn đến hàng phần chục là
| \(1,4\) | |
| \(1,3\) | |
| \(1,5\) | |
| \(1,6\) |
Một viên gạch hoa hình vuông cạnh \(40\) cm. Người ta đã dùng bốn đường parabol có chung đỉnh tại tâm của viên gạch để tạo ra bốn cánh hoa (phần tô đậm như hình vẽ).
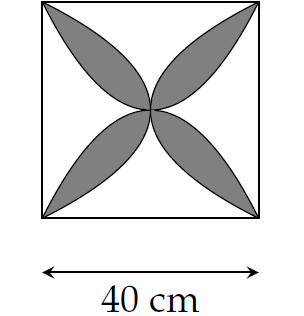
Diện tích của mỗi cánh hoa đó bằng
| \(200\) cm\(^2\) | |
| \(\dfrac{800}{3}\) cm\(^2\) | |
| \(\dfrac{400}{3}\) cm\(^2\) | |
| \(\dfrac{200}{3}\) cm\(^2\) |
Bạn An cần mua một chiếc gương có viền là đường parabol bậc hai (như hình vẽ).
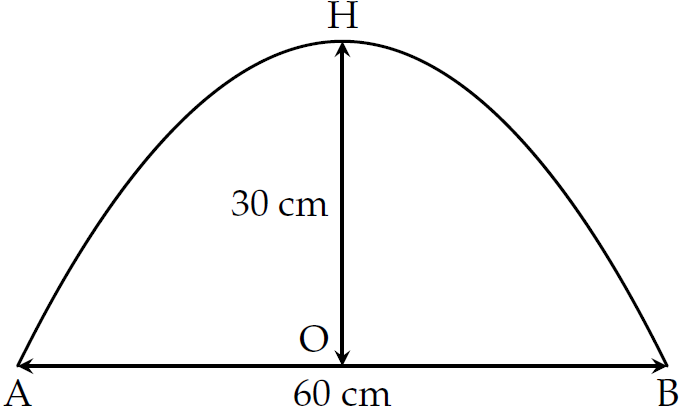
Biết rằng đoạn \(AB=60\) cm, \(OH=30\) cm. Diện tích của chiếc gương bạn An mua là
| \(1000\) cm\(^2\) | |
| \(1400\) cm\(^2\) | |
| \(1200\) cm\(^2\) | |
| \(900\) cm\(^2\) |
Một mảnh vườn hình tròn tâm \(O\) bán kính \(6\)m. Người ta cần trồng cây trên dải đất rộng \(6\)m nhận \(O\) làm tâm đối xứng, biết kinh phí trồng cây là \(70000\) đồng/m\(^2\).
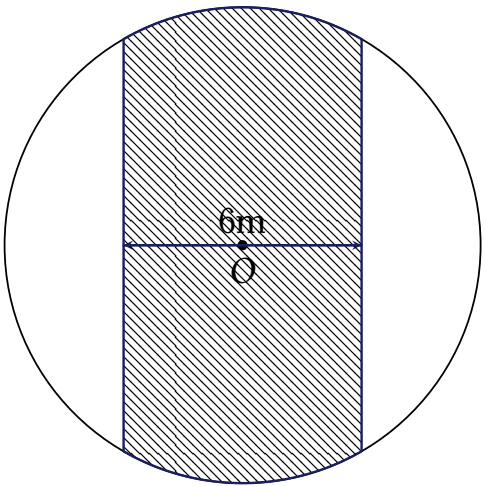
Hỏi cần bao nhiêu tiền để trồng cây trên dải đất đó?
| \(8.412.322\) đồng | |
| \(4.821.322\) đồng | |
| \(3.142.232\) đồng | |
| \(4.821.232\) đồng |
Câu lạc bộ bóng đá AS Roma dự định xây dựng sân vận động mới có tên là Stadio Dellta Roma để làm sân nhà cho đội bóng thay thế cho sân Olimpico. Hệ thống mái của sân vận động dự định được xây dựng có dạng hai hình elip như hình bên với elip lớn bên ngoài có có độ dài trục lớn là \(146\) mét, độ dài trục nhỏ là \(108\) mét; hình elip nhỏ bên trong có độ dài trục lớn là \(110\) mét, độ dài trục nhỏ là \(72\) mét.
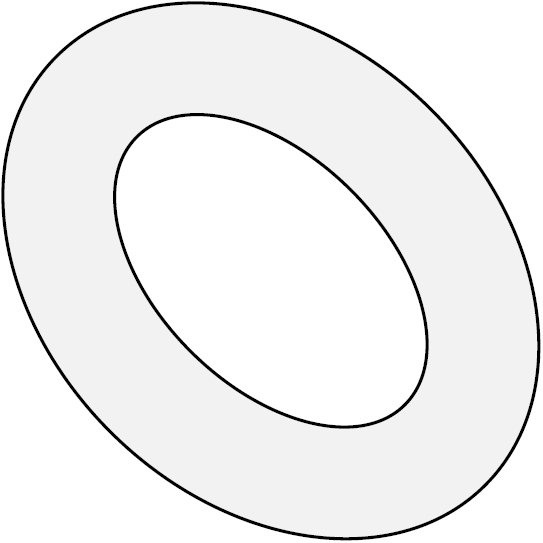
Giả sử chi phí vật liệu là \(100\)$ mỗi mét vuông. Tính chi phí cần thiết để xây dựng hệ thống mái sân.
| \(98100\) | |
| \(98100\pi\) | |
| \(196200\) | |
| \(196200\pi\) |
Trong không gian \(Oxyz\), cho hai điểm \(A(4;1;-2)\) và \(B(5;9;3)\). Phương trình mặt phẳng trung trực của đoạn \(AB\) là
| \(2x+6y-5z+40=0\) | |
| \(x+8y-5z-41=0\) | |
| \(x-8y-5z-35=0\) | |
| \(x+8y+5z-47=0\) |
