Cho \(I=\displaystyle\int\limits_{1}^{2}x\sqrt{4-x^2}\mathrm{\,d}x\) và \(t=\sqrt{4-x^2}\). Khẳng định nào sau đây sai?

	\(I=\sqrt{3}\)
	\(I=\dfrac{t^2}{2}\bigg|_0^{\sqrt{3}}\)
	\(I=\displaystyle\int\limits_{0}^{\sqrt{3}}t^2\mathrm{\,d}t\)
	\(I=\dfrac{t^3}{3}\bigg|_0^{\sqrt{3}}\)

Tích phân \(I=\displaystyle\int\limits_{1}^{2}\left(x^2+\dfrac{x}{x+1}\right)\mathrm{\,d}x\) có giá trị là

	\(I=\dfrac{10}{3}+\ln2-\ln3\)
	\(I=\dfrac{10}{3}+\ln2+\ln3\)
	\(I=\dfrac{10}{3}-\ln2+\ln3\)
	\(I=\dfrac{10}{3}-\ln2-\ln3\)

Biết rằng tích phân \(\displaystyle\int\limits_{0}^{1}(2x+1)\mathrm{e}^x\mathrm{\,d}x=a+b\mathrm{e}\) với \(a,\,b\in\mathbb{Z}\). Tích \(ab\) bằng

	\(1\)
	\(-1\)
	\(-15\)
	\(20\)

Khẳng định nào sau đây đúng?

	\(\displaystyle\int\limits_{-2}^{2}f(x)\mathrm{\,d}x=-\displaystyle\int\limits_{0}^{2}\left[f(x)+f(-x)\right]\mathrm{\,d}x\)
	\(\displaystyle\int\limits_{-2}^{2}f(x)\mathrm{\,d}x=-2\displaystyle\int\limits_{0}^{2}f(x)\mathrm{\,d}x\)
	\(\displaystyle\int\limits_{-2}^{2}2f(x)\mathrm{\,d}x=2\displaystyle\int\limits_{-2}^{2}f(x)\mathrm{\,d}x\)
	\(\displaystyle\int\limits_{-2}^{2}f(x)\mathrm{\,d}x=2\displaystyle\int\limits_{0}^{2}f(x)\mathrm{\,d}x\)

Cho \(f(x)\) là hàm số chẵn trên \(\mathbb{R}\) thỏa mãn \(\displaystyle\int\limits_{-3}^{0}f(x)\mathrm{\,d}x=2\). Chọn mệnh đề đúng.

	\(\displaystyle\int\limits_{-3}^{3}f(x)\mathrm{\,d}x=4\)
	\(\displaystyle\int\limits_{3}^{0}f(x)\mathrm{\,d}x=2\)
	\(\displaystyle\int\limits_{0}^{3}f(x)\mathrm{\,d}x=-2\)
	\(\displaystyle\int\limits_{-3}^{3}f(x)\mathrm{\,d}x=2\)

Giả sử \(\displaystyle\int\limits_{0}^{9}f(x)\mathrm{\,d}x=37\) và \(\displaystyle\int\limits_{9}^{0}g(x)\mathrm{\,d}x=16\). Khi đó, \(I=\displaystyle\int\limits_{0}^{9}\left[2f(x)+3g(x)\right]\mathrm{\,d}x\) bằng

	\(122\)
	\(26\)
	\(143\)
	\(58\)

Biết \(\displaystyle\int f(u)\mathrm{\,d}u=F(u)+C\). Mệnh đề nào dưới đây đúng?

	\(\displaystyle\int f(2x-1)\mathrm{\,d}x=2F(2x-1)+C\)
	\(\displaystyle\int f(2x-1)\mathrm{\,d}x=2F(x)-1+C\)
	\(\displaystyle\int f(2x-1)\mathrm{\,d}x=\dfrac{1}{2}F(2x-1)+C\)
	\(\displaystyle\int f(2x-1)\mathrm{\,d}x=F(2x-1)+C\)

Tìm nguyên hàm của hàm số \(f(x)=x\mathrm{e}^x\).

	\(\displaystyle\int f(x)\mathrm{\,d}x=(x+1)\mathrm{e}^x+C\)
	\(\displaystyle\int f(x)\mathrm{\,d}x=(x-1)\mathrm{e}^x+C\)
	\(\displaystyle\int f(x)\mathrm{\,d}x=x\mathrm{e}^x+C\)
	\(\displaystyle\int f(x)\mathrm{\,d}x=x^2\mathrm{e}^x+C\)

Tìm hàm số \(F(x)\) biết \(F'(x)=\sin2x\) và \(F\left(\dfrac{\pi}{2}\right)=1\).

	\(F(x)=\dfrac{1}{2}\cos2x+\dfrac{3}{2}\)
	\(F(x)=2x-\pi+1\)
	\(F(x)=-\dfrac{1}{2}\cos2x+\dfrac{1}{2}\)
	\(F(x)=-\cos2x\)

Hàm số nào dưới đây là nguyên hàm của hàm số \(f(x)=\dfrac{1}{1-x}\)?

	\(F(x)=-\dfrac{1}{4}\ln|4-4x|+3\)
	\(F(x)=-\ln|1-x|+4\)
	\(F(x)=\ln|1-x|+2\)
	\(F(x)=\dfrac{1}{2}\ln\left(x^2-2x+1\right)+5\)

Tìm nguyên hàm của hàm số \(f(x)=5^x\).

	\(\displaystyle\int f(x)\mathrm{\,d}x=5^x\ln5+C\)
	\(\displaystyle\int f(x)\mathrm{\,d}x=5^x+C\)
	\(\displaystyle\int f(x)\mathrm{\,d}x=\dfrac{5^x}{\ln x}+C\)
	\(\displaystyle\int f(x)\mathrm{\,d}x=\dfrac{5^x}{\ln5}+C\)

Cho ba số phức \(z_1,\,z_2,\,z_3\) phân biệt thỏa mãn \(\left|z_1\right|=\left|z_2\right|=\left|z_3\right|=3\) và \(\overline{z_1}+\overline{z_2}=\overline{z_3}\). Biết \(z_1,\,z_2,\,z_3\) lần lượt được biểu diễn bởi các điểm \(A,\,B,\,C\) trên mặt phẳng phức. Tính góc \(\widehat{ACB}\).

	\(150^\circ\)
	\(90^\circ\)
	\(120^\circ\)
	\(45^\circ\)

Với các số phức \(z\) thỏa mãn \(\left|z-2+i\right|=4\), tập hợp điểm biểu diễn các số phức \(z\) là một đường tròn. Tìm bán kính \(R\) của đường tròn đó.

	\(R=8\)
	\(R=16\)
	\(R=2\)
	\(R=4\)

Cho \(z\) là một số thuần ảo khác \(0\). Mệnh đề nào sau đây đúng?

	\(\overline{z}\) là số thực
	Phần ảo của \(z\) bằng \(0\)
	\(z=\overline{z}\)
	\(z+\overline{z}=0\)

Cho số phức \(z_1=1+2i\), \(z_2=3-i\). Tìm số phức liên hợp của số phức \(w=z_1+z_2\).

	\(\overline{w}=4-i\)
	\(\overline{w}=4+i\)
	\(\overline{w}=-4+i\)
	\(\overline{w}=-4-i\)

Cho các số phức \(z_1=3i\), \(z_2=-1-3i\) và \(z_3=m-2i\). Tập giá trị của tham số \(m\) để số phức \(z_3\) có môđun nhỏ nhất trong \(3\) số phức đã cho là

	\(\left[-\sqrt{5};\sqrt{5}\right]\)
	\(\left(-\sqrt{5};\sqrt{5}\right)\)
	\(\left\{-\sqrt{5};\sqrt{5}\right\}\)
	\(\left(-\infty;\sqrt{5}\right)\cup\left(\sqrt{5};+\infty\right)\)

Trong mặt phẳng với hệ tọa độ \(Oxy\), cho các điểm \(A(4;0)\), \(B(1;4)\) và \(C(1;-1)\). Gọi \(G\) là trọng tâm của tam giác \(ABC\). Biết rằng \(G\) là điểm biểu diễn số phức \(z\). Mệnh đề nào sau đây là đúng?

	\(z=3-\dfrac{3}{2}i\)
	\(z=3+\dfrac{3}{2}i\)
	\(z=2-i\)
	\(z=2+i\)

Điểm biểu diễn của các số phức \(z=7+bi\) với \(b\in\mathbb{R}\) nằm trên đường thẳng có phương trình là

	\(y=x+7\)
	\(y=7\)
	\(x=7\)
	\(y=x\)

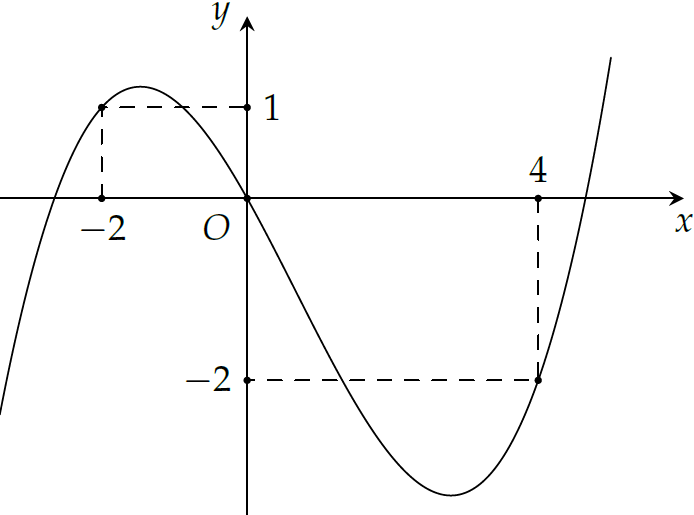
Cho hàm số \(f(x)\). Hàm số \(y=f'(x)\) có đồ thị như hình trên. Hàm số \(g(x)=f(1-2x)+x^2-x\) nghịch biến trên khoảng nào dưới đây?

	\(\left(1;\dfrac{3}{2}\right)\)
	\(\left(0;\dfrac{1}{2}\right)\)
	\(\left(-2;-1\right)\)
	\(\left(2;3\right)\)

Cho khối chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(A\), \(AB=a\), \(\widehat{SBA}=\widehat{SCA}=90^\circ\), góc giữa hai mặt phẳng \(\left(SAB\right)\) và \(\left(SAC\right)\) bằng \(60^\circ\). Thể tích khối chóp đã cho bằng

	\(a^3\)
	\(\dfrac{a^3}{3}\)
	\(\dfrac{a^3}{2}\)
	\(\dfrac{a^3}{6}\)