Giới hạn của hàm số $$f(x)=\begin{cases}
\dfrac{x^2-4x+3}{|x-3|} &\text{khi }x>3 \\
|3x-11| &\text{khi }x\leq3
\end{cases}$$tại \(x_0=3\) bằng

	\(-2\)
	\(2\)
	\(3\)
	Không tồn tại

Giới hạn của hàm số $$f(x)=\begin{cases}
2x+5 &\text{khi }x\geq4\\
\dfrac{x^2-16}{x-4} &\text{khi }x<4
\end{cases}$$tại \(x_0=4\) bằng

	\(13\)
	\(8\)
	\(4\)
	Không tồn tại

Giới hạn của hàm số $$f(x)=\begin{cases}
x^2+x+1 &\text{khi }x\leq1\\
x^2-4 &\text{khi }x>1
\end{cases}$$tại \(x_0=1\) bằng

	\(1\)
	\(-3\)
	\(3\)
	Không tồn tại

Giới hạn của hàm số $$f(x)=\begin{cases}
x^2+x+1 &\text{khi }x\leq1\\
5x^2-2 &\text{khi }x>1
\end{cases}$$tại \(x_0=1\) bằng

	\(1\)
	\(-3\)
	\(3\)
	Không tồn tại

Giới hạn \(\lim\limits_{x\to6}\dfrac{\sqrt{x+3}-3}{x-6}\) bằng

	\(0\)
	\(\dfrac{1}{6}\)
	\(\dfrac{166}{999}\)
	\(+\infty\)

Giới hạn \(\lim\limits_{x\to2}\dfrac{x^2-3x+2}{x^3-x^2+x-6}\) bằng

	\(0\)
	\(\dfrac{1}{7}\)
	\(\dfrac{1}{9}\)
	Không tồn tại

Giới hạn \(\lim\limits_{x\to1}\dfrac{x^2-3x+2}{x^2-1}\) bằng

	\(0\)
	\(-\dfrac{1}{2}\)
	\(+\infty\)
	Không tồn tại

Giới hạn \(\lim\limits_{x\to1}\dfrac{x^2-3x+2}{x^2+1}\) bằng

	\(0\)
	\(-\dfrac{1}{2}\)
	\(+\infty\)
	Không tồn tại

Giới hạn \(\lim\limits_{x\to-2}\sqrt{x+1}\) bằng

	\(1\)
	\(-1\)
	\(-2\)
	Không tồn tại

Đồ thị hàm số nào dưới đây có tiệm cận đứng \(x=1\) và đi qua điểm \(A(2;5)\)?

	\(y=\dfrac{2-3x}{1-x}\)
	\(y=\dfrac{x+13}{x+1}\)
	\(y=\dfrac{2x+1}{x-1}\)
	\(y=\dfrac{x+1}{x-1}\)

Tìm giao điểm của hai đường tiệm cận của đồ thị hàm số \(y=\dfrac{x-2}{x+2}\).

	\(M(2;1)\)
	\(N(-2;2)\)
	\(P(-2;-2)\)
	\(Q(-2;1)\)

Tọa độ giao điểm của hai đường tiệm cận của đồ thị hàm số \(y=\dfrac{3x-7}{x+2}\) là

	\((2;-3)\)
	\((-2;3)\)
	\((3;-2)\)
	\((-3;2)\)

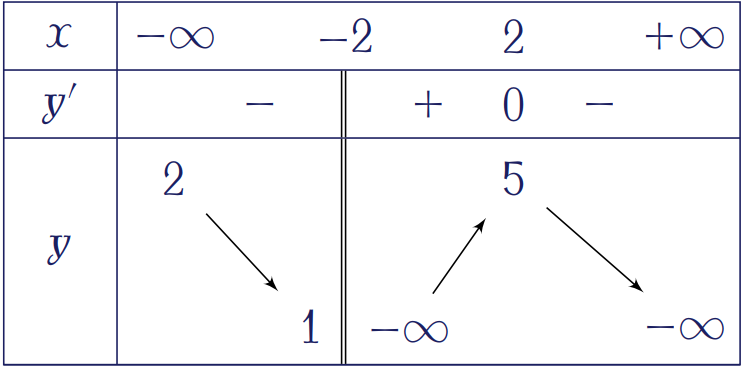
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình trên. Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là

	\(4\)
	\(2\)
	\(3\)
	\(1\)

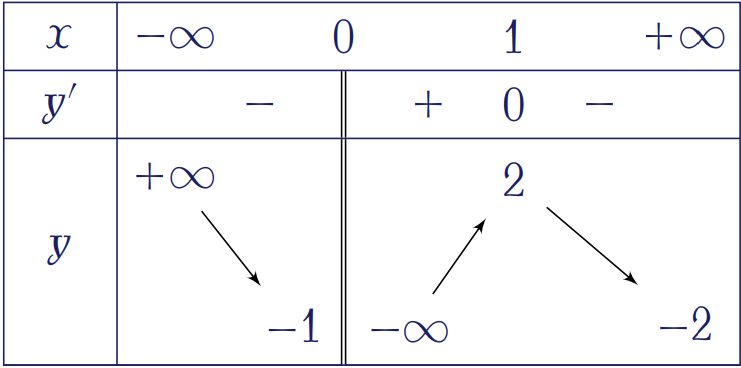
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình trên. Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là

	\(3\)
	\(4\)
	\(1\)
	\(2\)

Cho hàm số \(y=f(x)\) có bảng biến thiên như hình bên. Đồ thị của \(f(x)\) có

	\(2\) đường tiệm cận đứng là \(x=2\) và \(x=-4\)
	\(2\) đường tiệm cận ngang là \(y=2\) và \(y=-4\)
	\(2\) đường tiệm cận ngang là \(x=2\) và \(x=-4\)
	\(2\) đường tiệm cận đứng là \(y=2\) và \(y=-4\)

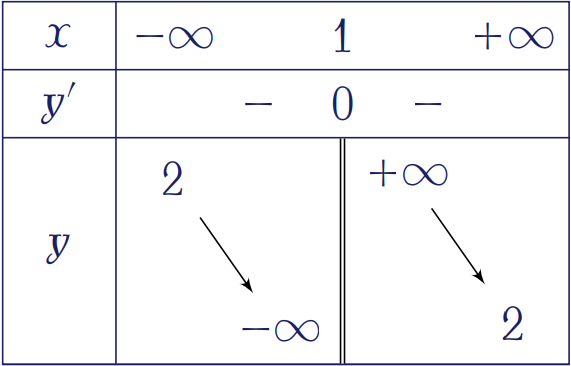
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình trên. Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng có phương trình

	\(x=2\)
	\(y=2\)
	\(x=1\)
	\(y=1\)

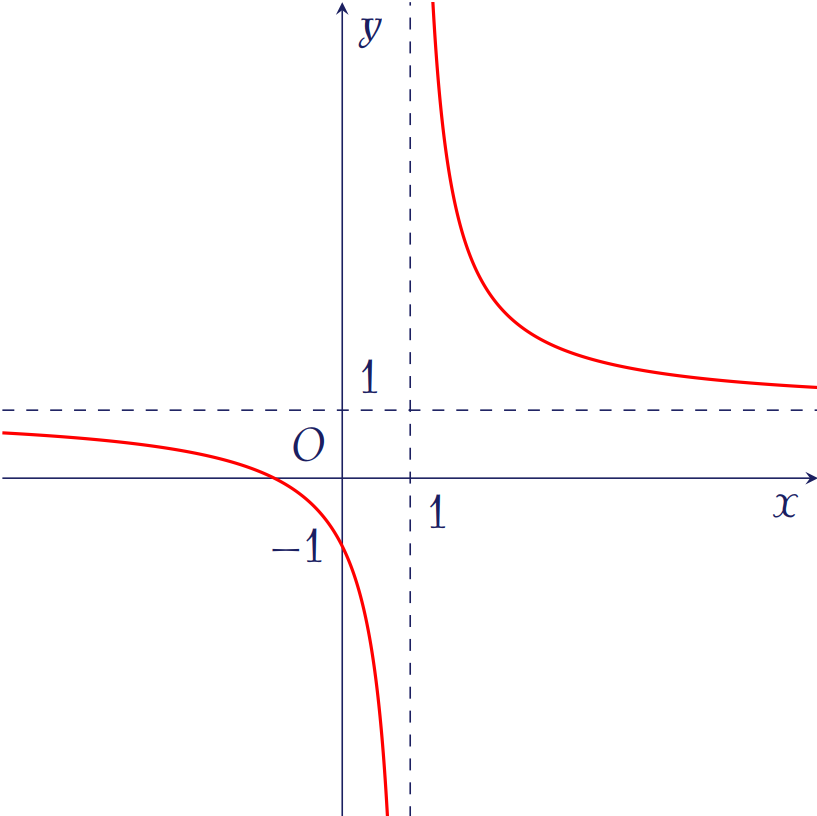
Đường cong trong hình trên là đồ thị của hàm số nào dưới đây?

	\(y=-x^3+3x+1\)
	\(y=\dfrac{x+1}{x-1}\)
	\(y=\dfrac{x-1}{x+1}\)
	\(y=x^3-3x-1\)

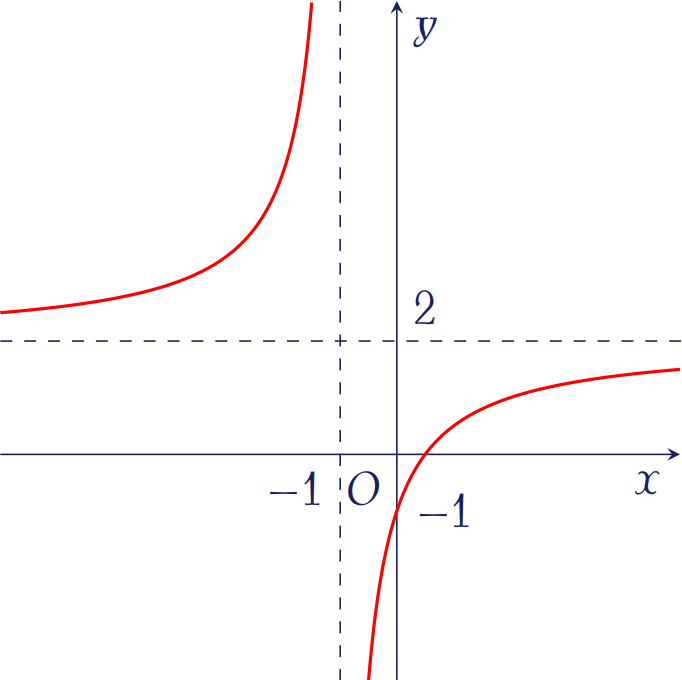
Đường cong trong hình trên là đồ thị của hàm số nào dưới đây?

	\(y=\dfrac{2x-1}{x+1}\)
	\(y=\dfrac{1-2x}{x+1}\)
	\(y=\dfrac{2x+1}{x-1}\)
	\(y=\dfrac{2x+1}{x+1}\)

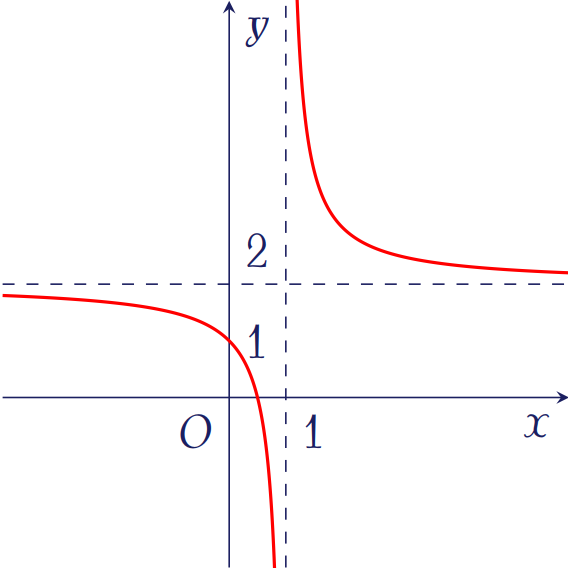
Cho hàm số \(y=\dfrac{ax-1}{bx+c}\) có đồ thị như hình trên. Tính giá trị biểu thức \(T=a+2b+3c\).

	\(T=1\)
	\(T=2\)
	\(T=3\)
	\(T=4\)

Biết rằng đồ thị hàm số \(y=\dfrac{(m-2n-3)x+5}{x-m-n}\) nhận hai trục tọa độ làm hai đường tiệm cận. Tính tổng \(S=m^2+n^2-2\).

	\(S=2\)
	\(S=0\)
	\(S=-1\)
	\(S=1\)