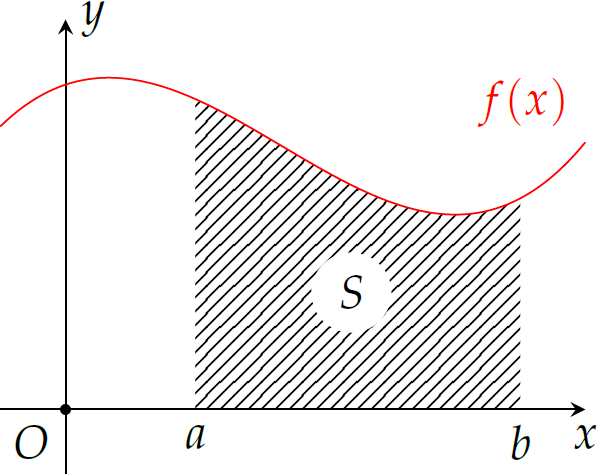
Diện tích hình phẳng \(S\) đối với hình vẽ trên là

	\(S=-\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x\)
	\(S=\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x\)
	\(S=\displaystyle\int\limits_{b}^{a}f(x)\mathrm{\,d}x\)
	\(S=\displaystyle\int\limits_{a}^{b}-f(x)\mathrm{\,d}x\)

Biết rằng \(\displaystyle\int\limits_{1}^{5}\dfrac{3}{x^2+3x}\mathrm{\,d}x=a\ln5+b\ln2\), (\(a,\,b\in\mathbb{Z}\)). Mệnh đề nào sau đây đúng?

	\(a+b=0\)
	\(a-b=0\)
	\(a+2b=0\)
	\(2a-b=0\)

Cho \(\displaystyle\int\limits_{\tfrac{\pi}{6}}^{\tfrac{\pi}{2}}\dfrac{\cos x}{\sin x+1}\mathrm{\,d}x=a\ln2+b\ln3\) (\(a,\,b\in\mathbb{Z}\)). Khi đó, giá trị của \(a\cdot b\) là

	\(2\)
	\(-2\)
	\(-4\)
	\(3\)

Kết quả của phép tính tích phân \(\displaystyle\int\limits_{0}^{1}\ln(2x+1)\mathrm{\,d}x=a\ln3+b\), (\(a,\,b\in\mathbb{Q}\)) khi đó giá trị của \(ab^3\) bằng

	\(-\dfrac{3}{2}\)
	\(3\)
	\(1\)
	\(\dfrac{3}{2}\)

Cho \(I=\displaystyle\int\limits_{0}^{\tfrac{\pi}{2}}\sin2x\mathrm{\,d}x\), \(J=\displaystyle\int\limits_{0}^{\tfrac{\pi}{2}}\sin x\mathrm{\,d}x\). Trong các mệnh đề sau, mệnh đề nào đúng?

	\(I>J\)
	\(I=J\)
	\(I< J\)
	\(I=2J\)

Cho tích phân \(\displaystyle\int\limits_{0}^{3}\dfrac{x}{1+\sqrt{1+x}}\mathrm{\,d}x\) và đặt \(t=\sqrt{1+x}\). Mệnh đề nào sau đây đúng?

	\(\displaystyle\int\limits_{1}^{2}\left(t^2-1\right)\mathrm{\,d}t\)
	\(\displaystyle\int\limits_{1}^{2}\left(2t^2+2t\right)\mathrm{\,d}t\)
	\(\displaystyle\int\limits_{1}^{2}\left(t^2+t\right)\mathrm{\,d}t\)
	\(\displaystyle\int\limits_{1}^{2}\left(2t^2-2t\right)\mathrm{\,d}t\)

Biết \(\displaystyle\int\limits_{1}^{2}f(x)\mathrm{\,d}x=2\) và \(\displaystyle\int\limits_{1}^{3}f(x)\mathrm{\,d}x=3\). Kết quả \(\displaystyle\int\limits_{3}^{2}f(x)\mathrm{\,d}x\) bằng bao nhiêu?

	\(3\)
	\(\dfrac{5}{2}\)
	\(-1\)
	\(1\)

Với \(a\neq0\). Cho biểu thức \(B=\displaystyle\int\limits_{-1}^{1}ax^2\mathrm{\,d}x\). Khẳng định nào sau đây sai?

	\(B=a\displaystyle\int\limits_{-1}^{1}x^2\mathrm{\,d}x\)
	\(B=-\displaystyle\int\limits_{1}^{-1}ax^2\mathrm{\,d}x\)
	\(B=\displaystyle\int\limits_{1}^{0}ax^2\mathrm{\,d}x+\displaystyle\int\limits_{0}^{-1}ax^2\mathrm{\,d}x\)
	\(B=\dfrac{2a}{3}\)

Giả sử hàm số \(f\) liên tục trên khoảng \(\mathbb{K}\) và \(a,\,b,\,c\) là \(3\) số thực bất kỳ thuộc \(\mathbb{K}\). Khẳng định nào sau đây sai?

	\(\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x\neq\displaystyle\int\limits_{a}^{b}f(t)\mathrm{\,d}t\)
	\(\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x=-\displaystyle\int\limits_{b}^{a}f(t)\mathrm{\,d}t\)
	\(\displaystyle\int\limits_{a}^{a}f(x)\mathrm{\,d}x=0\)
	\(\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x=\displaystyle\int\limits_{a}^{c}f(x)\mathrm{\,d}x+\displaystyle\int\limits_{c}^{b}f(x)\mathrm{\,d}x\;\left(c\in(a;b)\right)\)

\(F(x)\) là một nguyên hàm của hàm số \(f(x)=\cot x\) và \(F\left(\dfrac{\pi}{2}\right)=0\). Giá trị của \(F\left(\dfrac{\pi}{6}\right)\) bằng

	\(-\ln\left(\dfrac{\sqrt{3}}{2}\right)\)
	\(\ln\left(\dfrac{\sqrt{3}}{2}\right)\)
	\(\ln2\)
	\(-\ln2\)

Cho \(F(x)\) là một nguyên hàm của hàm số \(f(x)=\mathrm{e}^{3x}\) thỏa \(F(0)=1\). Mệnh đề nào sau đây là đúng?

	\(F(x)=\dfrac{1}{3}\mathrm{e}^{3x}+\dfrac{2}{3}\)
	\(F(x)=\dfrac{1}{3}\mathrm{e}^{3x}+1\)
	\(F(x)=\dfrac{1}{3}\mathrm{e}^{3x}\)
	\(F(x)=-\dfrac{1}{3}\mathrm{e}^{3x}+\dfrac{4}{3}\)

Một nguyên hàm \(F(x)\) của hàm số \(f(x)=\dfrac{\mathrm{e}^x}{\mathrm{e}^x+2}\) thỏa \(F(0)=-\ln3\) là

	\(\ln\left(\mathrm{e}^x+2\right)+\ln3\)
	\(\ln\left(\mathrm{e}^x+2\right)+2\ln3\)
	\(\ln\left(\mathrm{e}^x+2\right)-\ln3\)
	\(\ln\left(\mathrm{e}^x+2\right)-2\ln3\)

Nguyên hàm của hàm số \(f(x)=\dfrac{2x^2+1}{x}\) là

	\(x^2+\ln|x|\)
	\(x^2+\ln x+C\)
	\(x^2-\ln|x|+C\)
	\(x^2+\ln|x|+C\)

Khẳng định nào sau đây là khẳng định sai?

	\(\displaystyle\int\cos x\mathrm{\,d}x=\sin x+C\)
	\(\displaystyle\int\dfrac{1}{x^2}\mathrm{\,d}x=-\dfrac{1}{x}+C\)
	\(\displaystyle\int\dfrac{1}{2\sqrt{x}}\mathrm{\,d}x=\sqrt{x}+C\)
	\(\displaystyle\int a^x\mathrm{\,d}x=a^x\cdot\ln a+C\) (\(a>0,\,a\neq1\))

Cặp số nào sau đây có tính chất "Có một hàm số là nguyên hàm của hàm số còn lại"?

	\(\tan x\) và \(\dfrac{1}{\sin^2x^2}\)
	\(\sin x\) và \(\cos x\)
	\(\mathrm{e}^x\) và \(\mathrm{e}^{-x}\)
	\(x^2\) và \(x\)

Một ô tô đang chạy với vận tốc \(54\) km/h thì tăng tốc chuyển động nhanh dần đều với gia tốc \(a(t)=3t-8\) (m/s\(^2\)) trong đó \(t\) là khoảng thời gian tính bằng giây. Quãng đường mà ô tô đi được sau \(10\) s kể từ lúc tăng tốc là

	\(540\) m
	\(150\) m
	\(250\) m
	\(246\) m

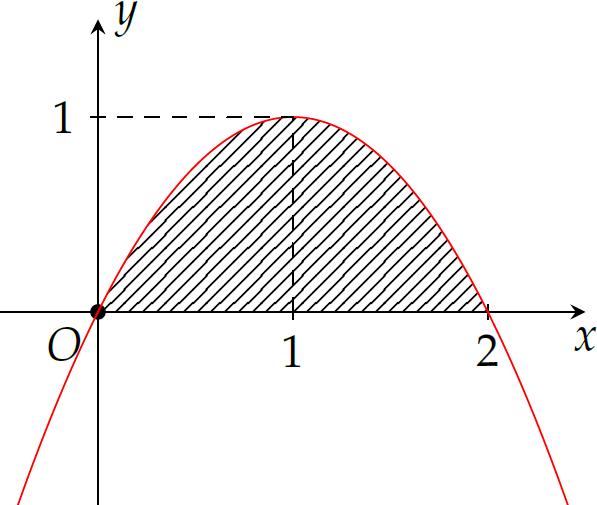
Cho hàm bậc hai \(y=f(x)\) có đồ thị như hình bên. Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số \(y=f(x)\) và \(Ox\) quanh \(Ox\).

	\(\dfrac{4\pi}{3}\)
	\(-\dfrac{12\pi}{15}\)
	\(\dfrac{16\pi}{15}\)
	\(\dfrac{16\pi}{5}\)

Gọi \(V\) là thể tích của khối tròn xoay do hình phẳng giới hạn bởi các đường sau quay quanh trục hoành: \(y=\sin x\), \(y=0\), \(x=0\), \(x=12\pi\). Mệnh đề nào dưới đây đúng?

	\(V=\pi\displaystyle\int\limits_{0}^{12\pi}\left(\sin x\right)^2\mathrm{\,d}x\)
	\(V=\pi\displaystyle\int\limits_{0}^{12\pi}\sin x\mathrm{\,d}x\)
	\(V=\pi^2\displaystyle\int\limits_{0}^{12\pi}\left(\sin x\right)^2\mathrm{\,d}x\)
	\(V=\pi^2\displaystyle\int\limits_{0}^{12\pi}\sin x\mathrm{\,d}x\)

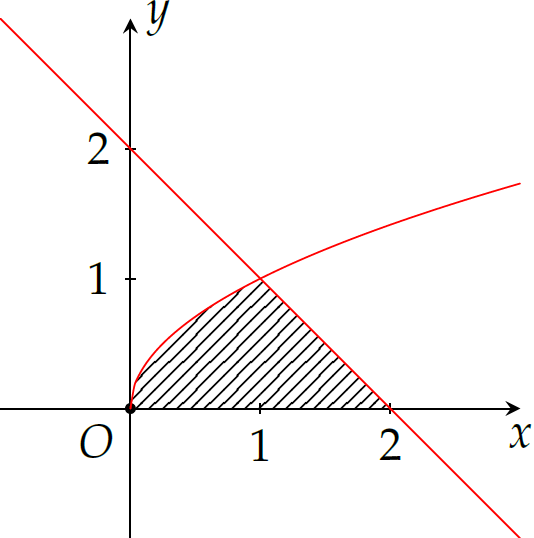
Cho \((H)\) là hình phẳng giới hạn bởi đồ thị của các hàm số \(y=\sqrt{x}\), \(y=0\), \(y=2-x\). Diện tích của \((H)\) là

	\(\dfrac{4\sqrt{2}-1}{3}\)
	\(\dfrac{8\sqrt{2}+3}{6}\)
	\(\dfrac{7}{6}\)
	\(\dfrac{5}{6}\)

Tính diện tích hình phẳng giới hạn bởi \(\left(\mathscr{C}\right)\colon y=x^4-2x^2+1\) và trục hoành.

	\(\dfrac{8}{15}\)
	\(-\dfrac{15}{16}\)
	\(\dfrac{15}{8}\)
	\(\dfrac{16}{15}\)