Một trang trại mỗi ngày thu hoạch được một tấn rau. Mỗi ngày, nếu bán rau với giá \(30000\) đồng/kg thì hết sạch rau, nếu giá bán cứ tăng thêm \(1000\) đồng/kg thì số rau thừa lại tăng thêm \(20\) kg. Số rau thừa này được thu mua làm thức ăn chăn nuôi với giá \(2000\) đồng/kg. Hỏi số tiền bán rau nhiều nhất mà trang trại có thể thu được mỗi ngày là bao nhiêu?
| \(32.420.000\) đồng | |
| \(32.400.000\) đồng | |
| \(34.400.000\) đồng | |
| \(34.240.000\) đồng |
Một ngọn hải đăng đặt tại vị trí \(A\) cách bờ biển \(BC=5\) km. Trên bờ biển có một cái kho ở vị trí \(C\) cách \(B\) \(7\) km. Người gác hải đăng có thể chèo đò từ \(A\) đến vị trí \(M\) trên bờ biển với vận tốc \(4\) km/h rồi đi bộ đến \(C\) với vận tốc \(6\) km/h.

Vị trí của điểm \(M\) phải cách \(B\) bao nhiêu km để người gác hải đăng đến \(C\) nhanh nhất?
| \(0\) km | |
| \(\dfrac{14+5\sqrt{5}}{12}\) km | |
| \(2\sqrt{5}\) km | |
| \(7\) km |
Tìm giá trị lớn nhất của hàm số \(f(x)=-x^4-3x^2+2020\) trên \(\mathbb{R}\).
| \(\max\limits_{\mathbb{R}}f(x)=2020\) | |
| \(\max\limits_{\mathbb{R}}f(x)=2021\) | |
| \(\max\limits_{\mathbb{R}}f(x)=2019\) | |
| \(\max\limits_{\mathbb{R}}f(x)=2018\) |
Hàm số \(y=x^4+2x^2-3\)
| không có giá trị lớn nhất và giá trị nhỏ nhất | |
| không có cực trị | |
| có giá trị nhỏ nhất | |
| có giá trị lớn nhất |
Tìm giá trị nhỏ nhất \(m\) của hàm số \(y=x-1+\dfrac{4}{x-1}\) trên khoảng \((1;+\infty)\).
| \(m=5\) | |
| \(m=4\) | |
| \(m=2\) | |
| \(m=3\) |
Giá trị nhỏ nhất của hàm số \(y=x^2+2x+5\) trên nửa khoảng \([-4;+\infty)\) là
| \(13\) | |
| \(-17\) | |
| \(4\) | |
| \(-9\) |
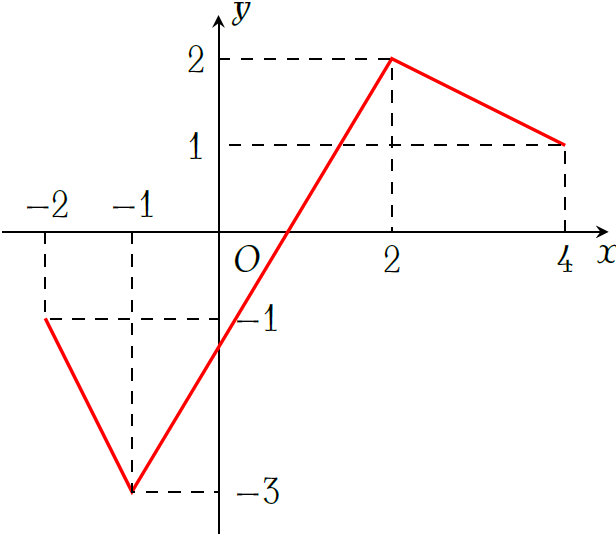
Cho hàm số \(y=f(x)\) có đồ thị như hình vẽ. Tìm \(\max\limits_{[-2;4]}\left|f(x)\right|\).
| \(\left|f(0)\right|\) | |
| \(2\) | |
| \(3\) | |
| \(1\) |
Gọi \(M,\,m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=x+\dfrac{1}{x}\) trên đoạn \(\left[\dfrac{1}{2};3\right]\). Khi đó \(M+m\) bằng
| \(\dfrac{9}{2}\) | |
| \(\dfrac{35}{6}\) | |
| \(\dfrac{7}{2}\) | |
| \(\dfrac{16}{3}\) |
Cho hàm số \(y=\dfrac{3x-1}{x+2}\). Gọi \(M,\,m\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn \([0;2]\). Khi đó \(4M-2m\) bằng
| \(10\) | |
| \(6\) | |
| \(5\) | |
| \(4\) |
Cho hàm số \(y=f(x)\) liên tục trên đoạn \([-3;2]\) và có bảng biến thiên như sau: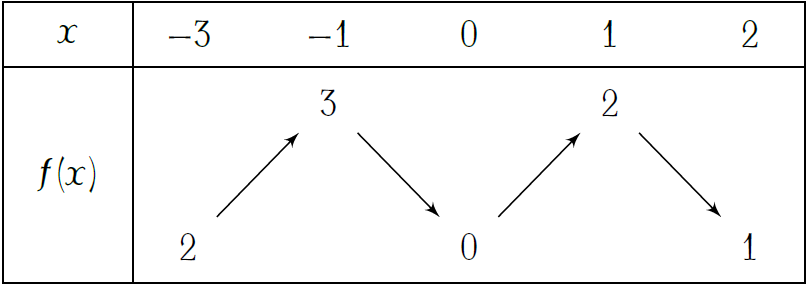
Gọi \(M,\,m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của \(f(x)\) trên đoạn \([-1;2]\). Tính \(M+m\).
| \(3\) | |
| \(2\) | |
| \(1\) | |
| \(4\) |
Gọi \(M,\,N\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y=x^3-3x^2+1\) trên đoạn \([1;2]\). Khi đó tổng \(M+N\) bằng
| \(2\) | |
| \(-2\) | |
| \(0\) | |
| \(-4\) |
Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=x\sqrt{1-x^2}\). Khi đó \(M-m\) bằng
| \(1\) | |
| \(2\) | |
| \(4\) | |
| \(3\) |
Giá trị lớn nhất của hàm số \(y=\sqrt{1-x^2}\) bằng
| \(1\) | |
| \(0\) | |
| \(-1\) | |
| \(2\) |
Tìm tập giá trị \(T\) của hàm số $$y=\sqrt{x-1}+\sqrt{9-x}$$
| \(T=[1;9]\) | |
| \(T=\left[0;2\sqrt{2}\right]\) | |
| \(T=(1;9)\) | |
| \(T=\left[2\sqrt{2};4\right]\) |
Giá trị nhỏ nhất \(m\) của hàm số \(y=x^3-3x+5\) trên đoạn \([2;4]\) là
| \(0\) | |
| \(5\) | |
| \(7\) | |
| \(3\) |
Tìm giá trị nhỏ nhất của hàm số \(y=\dfrac{x+3}{2x-3}\) trên đoạn \([2;5]\).
| \(\dfrac{7}{8}\) | |
| \(\dfrac{8}{7}\) | |
| \(5\) | |
| \(\dfrac{2}{7}\) |
Tìm giá trị nhỏ nhất của hàm số \(y=\dfrac{x+1}{x-1}\) trên đoạn \([2;3]\).
| \(-3\) | |
| \(3\) | |
| \(2\) | |
| \(4\) |
Tìm giá trị lớn nhất của hàm số \(y=\dfrac{3x-1}{x-3}\) trên đoạn \([0;2]\).
| \(-\dfrac{1}{3}\) | |
| \(-5\) | |
| \(5\) | |
| \(\dfrac{1}{3}\) |
Hàm số nào sau đây không có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn \([-2;2]\).
| \(y=\dfrac{x-1}{x+1}\) | |
| \(y=x^2\) | |
| \(y=1-x\) | |
| \(y=x^3+2\) |
Tìm giá trị lớn nhất của hàm số $$y=3+\sqrt{x^2-2x+8}$$trên đoạn \([-2;2]\).
| \(7\) | |
| \(9\) | |
| \(3+2\sqrt{2}\) | |
| \(3+\sqrt{7}\) |
