Tìm tập hợp giá trị của tham số $m$ để hàm số $y=x^3-mx^2-(m-6)x+1$ đồng biến trên khoảng $(0;4)$.
| $(-\infty;6]$ | |
| $(-\infty;3]$ | |
| $(-\infty;3)$ | |
| $[3;6]$ |
Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$, có bảng xét dấu đạo hàm như sau:

Hàm số $y=3f(2x-1)-4x^3+15x^2-18x+1$ đồng biến trên khoảng nào dưới đây?
| $(3;+\infty)$ | |
| $\left(1;\dfrac{3}{2}\right)$ | |
| $\left(\dfrac{5}{2};3\right)$ | |
| $\left(2;\dfrac{5}{2}\right)$ |
Cho hàm số $f(x)$ có đạo hàm liên tục trên $\mathbb{R}$. Đồ thị hàm số $f'(x)$ được cho như hình vẽ.
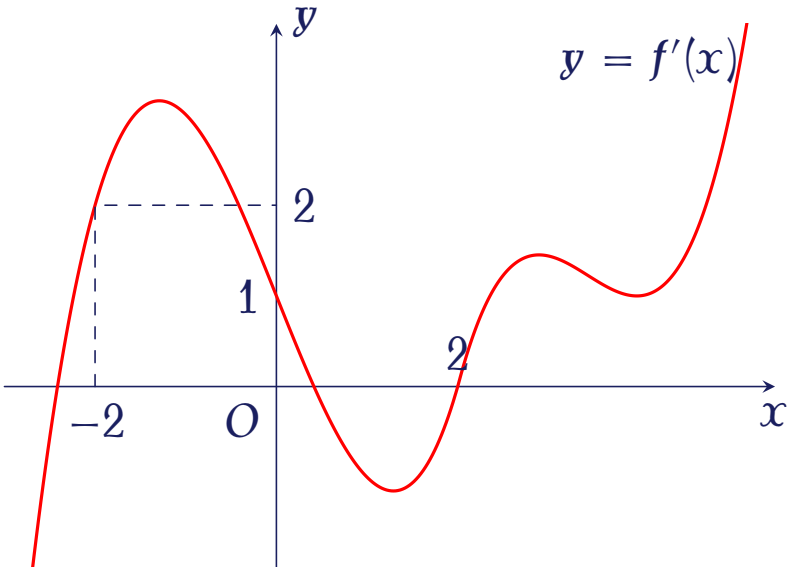
Hàm số $g(x)=4f(x)+x^2-4x+2022$ đồng biến trên khoảng nào sau đây?
| $[-2;0]$ và $[2;+\infty)$ | |
| $(-\infty;-2]$ và $[0;2]$ | |
| $[-2;2]$ | |
| $(-\infty;-2]$ và $[2;+\infty)$ |
Cho hàm số $f$ có đạo hàm liên tục trên $(-1;3)$. Bảng biến thiên của hàm số $f'(x)$ như hình vẽ.
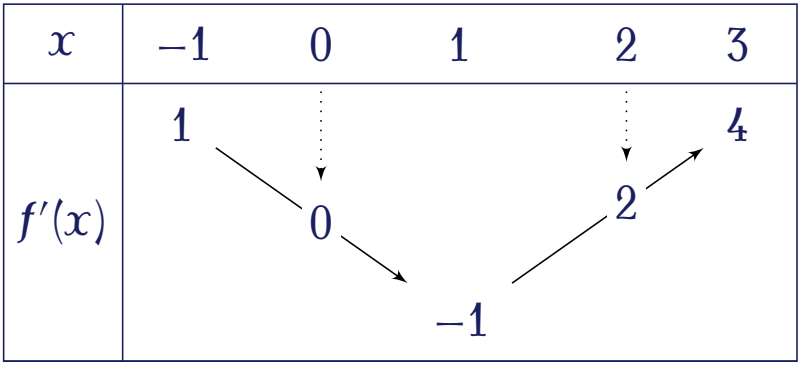
Hàm số $g(x)=f\left(1-\dfrac{x}{2}\right)+x$ nghịch biến trên khoảng nào trong các khoảng sau?
| $(-4;-2)$ | |
| $(2;4)$ | |
| $(-2;0)$ | |
| $(0;2)$ |
Cho hàm bậc bốn $y=f(x)$ có đồ thị $f'(x)$ như hình vẽ bên.
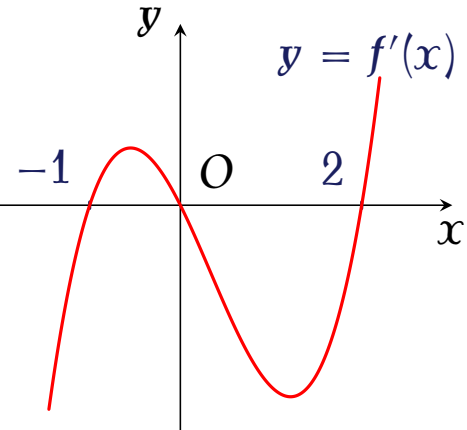
Hàm số $y=f(1-3x)-4$ nghịch biến trên khoảng
| $\left(-\dfrac{1}{3};\dfrac{1}{3}\right)$ | |
| $(0;2)$ | |
| $(-\infty;-1)$ | |
| $\left(\dfrac{1}{3};\dfrac{2}{3}\right)$ |
Cho hàm số bậc bốn $y=f(x)$ thỏa mãn $f(0)=0$. Hàm số $y=f'(x)$ có đồ thị như hình vẽ.
Hàm số $g(x)=\left|2f\big(x^2+x\big)-x^4-2x^3+x^2+2x\right|$ có bao nhiêu cực trị?
| $4$ | |
| $5$ | |
| $6$ | |
| $7$ |
Cho hàm số bậc bốn $f(x)=ax^4+bx^3+cx^2+dx+e$ có đồ thị như hình vẽ.
Số nghiệm của phương trình $f\big(f(x)\big)+1=0$ là
| $3$ | |
| $5$ | |
| $4$ | |
| $6$ |
Hàm số nào dưới dây là hàm số đồng biến trên $\mathbb{R}$?
| $y=\left(\sqrt{2}-1\right)^x$ | |
| $y=\log_3x$ | |
| $y=\left(\dfrac{1}{3}\right)^x$ | |
| $y=3^x$ |
Gọi $M$ và $m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y=\dfrac{2x+3}{x-2}$ trên đoạn $[0;1]$. Tính giá trị $M+m$.
| $-2$ | |
| $\dfrac{7}{2}$ | |
| $-\dfrac{13}{2}$ | |
| $-\dfrac{17}{3}$ |
Cho hàm số $y=ax^3+bx^2+cx+d$ ($a,\,b,\,c,\,d\in\mathbb{R}$) có đồ thị là đường cong như hình vẽ bên.
Giá trị cực tiểu của hàm số đã cho bằng
| $0$ | |
| $-1$ | |
| $1$ | |
| $4$ |
Cho hàm số $y=f(x)$ xác định trên $\mathbb{R}\setminus\{1\}$ và có bảng biến thiên như sau :
Mệnh đề nào sau đây đúng?
| Hàm số đồng biến trên khoảng $\left(2;+\infty\right)$ | |
| Hàm số nghịch biến trên khoảng $\left(-\infty;2\right)$ | |
| Hàm số nghịch biến trên các khoảng $\left(-\infty;1\right)$ và $\left(1;+\infty\right)$ | |
| Hàm số nghịch biến trên $\mathbb{R}$ |
Trong các hàm số sau, hàm số nào có đồ thị như hình vẽ dưới đây?
| $y=x^3+x^2-x+1$ | |
| $y=\log_3x$ | |
| $y=\sqrt{x}$ | |
| $y=\dfrac{x+1}{x-2}$ |
Tiệm cận ngang của đồ thị hàm số $y=\dfrac{3x+1}{1-x}$ là đường thẳng có phương trình
| $y=3$ | |
| $y=-1$ | |
| $y=1$ | |
| $y=-3$ |
Tập xác định của hàm số $y=x^{-\pi}$ là
| $\left(-\infty;0\right)$ | |
| $\mathbb{R}\setminus\{0\}$ | |
| $\left[0;+\infty\right)$ | |
| $\left(0;+\infty\right)$ |
Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$ có bảng xét dấu đạo hàm như sau:
Số điểm cực đại của hàm số đã cho là
| $4$ | |
| $-2$ | |
| $2$ | |
| $5$ |
Điểm nào sau đây thuộc đồ thị hàm số $y=\dfrac{2x+1}{x+1}$?
| $M(0;1)$ | |
| $N(-1;0)$ | |
| $P(2;5)$ | |
| $Q(1;0)$ |
Cho hàm số $y=f(x)$ có đạo hàm $f'(x)=(x-7)\left(x^2-9\right)$, $\forall x\in\mathbb{R}$. Có bao nhiêu giá trị nguyên dương của tham số $m$ để hàm số $g(x)=f\left(\left|x^3+5x\right|+m\right)$ có ít nhất $3$ điểm cực trị?
| $6$ | |
| $7$ | |
| $5$ | |
| $4$ |
Cho hàm số $f(x)=x^3+ax^2+bx+c$ với $a,\,b,\,c$ là các số thực. Biết hàm số $g(x)=f(x)+f'(x)+f''(x)$ có hai giá trị cực trị là $-3$ và $6$. Diện tích hình phẳng giới hạn bởi các đường $y=\dfrac{f(x)}{g(x)+6}$ và $y=1$ bằng
| $2\ln3$ | |
| $\ln3$ | |
| $\ln18$ | |
| $2\ln2$ |
Cho hàm số bậc ba $y=f(x)$ có đồ thị là đường cong trong hình bên.
Số nghiệm thực phân biệt của phương trình $f\big(f(x)\big)=1$ là
| $9$ | |
| $3$ | |
| $6$ | |
| $7$ |
Cho hàm số $f(x)=\begin{cases}2x+5 &\text{khi }x\ge1\\ 3x^2+4 &\text{khi }x< 1\end{cases}$. Giả sử $F$ là nguyên hàm của $f$ trên $\mathbb{R}$ thỏa mãn $F(0)=2$. Giá trị của $F(-1)+2F(2)$ bằng
| $27$ | |
| $29$ | |
| $12$ | |
| $33$ |
