Một hộp chứa \(18\) quả cầu gồm \(8\) quả cầu màu xanh và \(10\) quả cầu màu trắng. Chọn ngẫu nhiên \(2\) quả cầu từ hộp đó. Tính xác suất để chọn được \(2\) quả cầu cùng màu.
Một bộ đề có \(10\) câu hỏi trắc nghiệm, trong đó có \(6\) câu Đại số và \(4\) câu Hình học. Bạn Nam bốc thăm chọn ngẫu nhiên \(3\) câu từ bộ đề. Hỏi xác suất để trong số ba câu bạn Nam chọn được có ít nhất một câu Hình học.
Có hai thùng đựng rượu Bầu Đá, một loại rượu nổi tiếng của thị xã An Nhơn, tỉnh Bình Định. Thùng thứ nhất đựng \(10\) chai gồm \(6\) chai rượu loại một và \(4\) chai rượu loại hai. Thùng thứ hai đựng \(8\) chai gồm \(5\) chai rượu loại một và \(3\) chai rượu loại hai. Lấy ngẫu nhiên mỗi thùng một chai, tính xác suất để lấy được ít nhất một chai rượu loại một. Biết rằng các chai rượu giống nhau về hình thức (rượu loại một và loại hai chỉ khác nhau về nồng độ cồn) và khả năng được chọn là như nhau.
Chọn ngẫu nhiên \(2\) học sinh từ một tổ có \(9\) học sinh. Biết rằng xác suất chọn được \(2\) học sinh nữ bằng \(\dfrac{5}{18}\), hỏi tổ đó có bao nhiêu học sinh nữ.
Lớp 11B có \(20\) học sinh gồm \(12\) nữ và \(8\) nam. Cần chọn ra \(2\) học sinh của lớp đi lao động. Tính xác suất để chọn ngẫu nhiên được \(2\) học sinh trong đó có cả nam và nữ.
Lấy ngẫu nhiên 1 thẻ từ một hộp chứa 20 thẻ, được đánh số từ 1 đến 20. Tìm xác suất để thẻ được lấy ra là số
- Chẵn
- Chia hết cho 3
- Lẻ và chia hết cho 3
Gieo một đồng xu (cân đối và đồng chất) 3 lần và quan sát sự xuất hiện của mặt sấp (S) và mặt ngửa (N).
- Xây dựng không gian mẫu
- Xác định các biến cố:
A: "Lần gieo đầu xuất hiện mặt sấp"
B: "Ba lần xuất hiện mặt như nhau"
C: "Đúng 2 lần xuất hiện mặt sấp"
D: "Ít nhất một lần xuất hiện mặt sấp"
Một hộp đựng 4 viên bi xanh, 3 viên bi đỏ và 2 viên bi vàng. Chọn ngẫu nhiên 2 viên bi. Tính xác suất để chọn được 2 viên bi cùng màu.
Trền bàn có một cốc nước hình trụ chứa đầy nước, có chiều cao bằng 3 lần đường kính của đáy; một viên bi và một khối nón đều bằng thủy tinh. Biết viên bi là một khối cầu có đường kính bằng đường kính của cốc nước. Người ta từ từ thả vào cốc nước viên bi và khối nón sao cho đỉnh khối nón nằm trên mặt cầu (như hình vẽ) thì thấy nước trong cốc tràn ra ngoài.
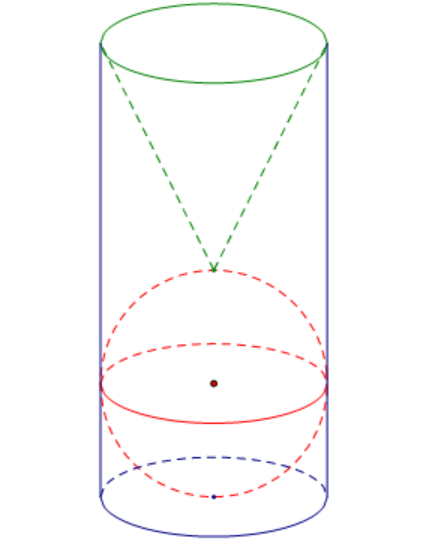
Tính tỉ số thể tích của lượng nước còn lại trong cốc và lượng nước ban đầu (bỏ qua bề dày của lớp vỏ thủy tinh).
Một chiếc cổng hình parabol dạng $y=-\dfrac{1}{2}x^2$ có chiều rộng chân cổng $d=8$m (như hình).
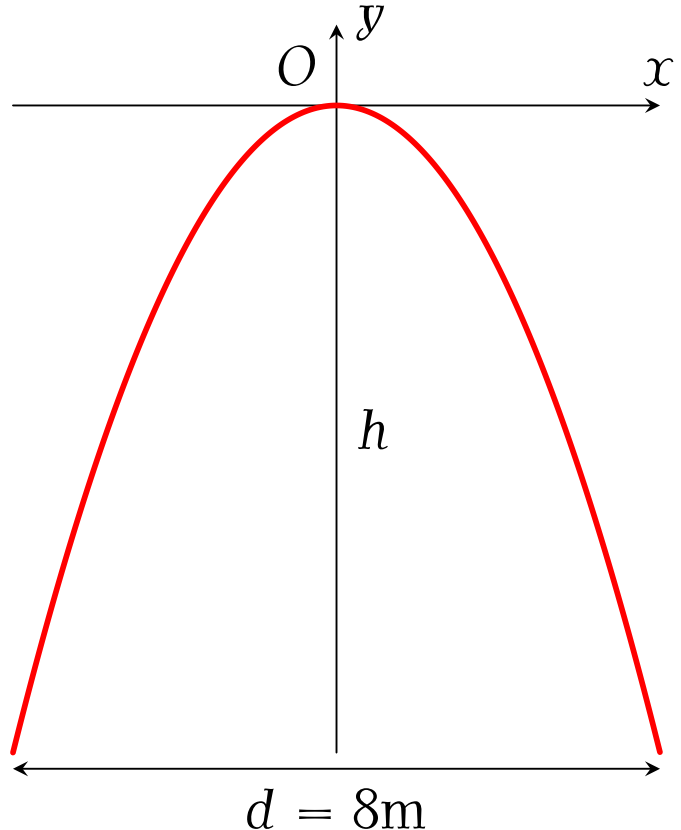
Hãy tính chiều cao $h$ của cổng.
 | $h=8$m |
 | $h=9$m |
 | $h=7$m |
 | $h=5$m |
Một vật chuyển động trong $3$ giờ với vận tốc $v$ (km/h) phụ thuộc thời gian $t$ (h) có đồ thị là một phần của đường parabol với đỉnh $I(2;9)$ và trục đối xứng song song với trục tung (như hình vẽ).
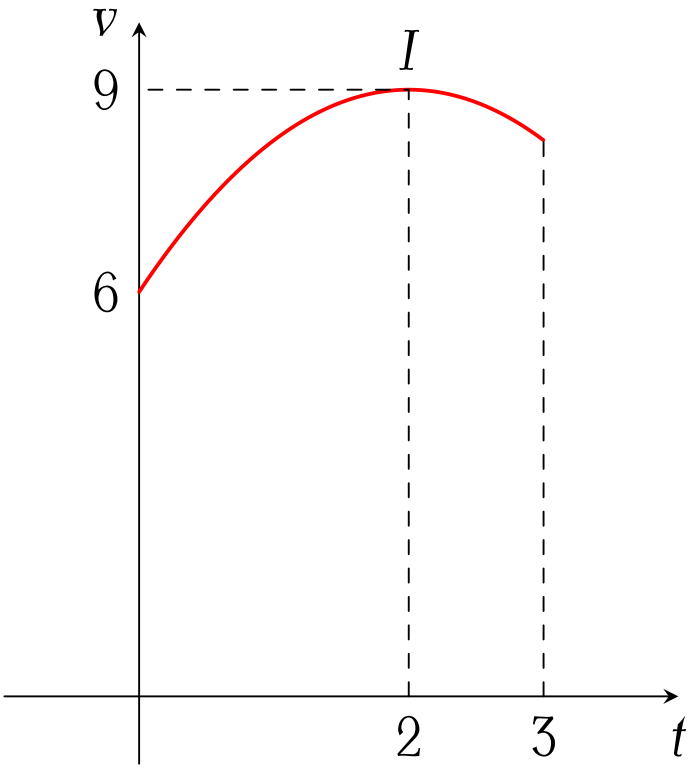
Vận tốc tức thời của vật tại thời điểm $2$ giờ $30$ phút sau khi vật bắt đầu chuyển động gần bằng giá trì nào nhất trong các giá trị sau:
| $8,7$ (km/h) |
| $8,8$ (km/h) |
| $8,6$ (km/h) |
| $8,5$ (km/h) |
Các kích thước của một bể bơi được cho trên hình vẽ (mặt nước có dạng hình chữ nhật).
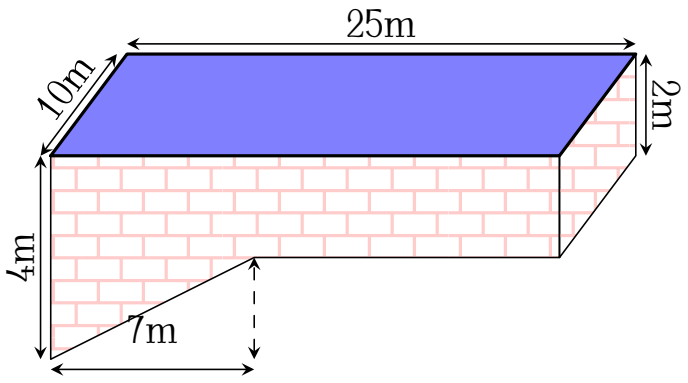
Hãy tính xem bể bơi chứa được bao nhiêu mét khối nước khi nó đầy ắp nước?
| $1000$m$^3$ |
| $640$m$^3$ |
| $570$m$^3$ |
| $500$m$^3$ |
Một người bán gạo muốn đóng một thùng tôn đựng gạo có thể tích không đổi bằng $8$m$^3$, thùng tôn hình hộp chữ nhật có đáy là hình vuông, không nắp. Trên thị trường, giá tôn làm đáy thùng là $100.000$ đồng/m$^2$, giá tôn làm thành xung quanh thùng là $50.000$ đồng/m$^2$. Hỏi người bán gạo đó cần đóng thùng đựng gạo với cạnh đáy bằng bao nhiêu để chi phí mua nguyên liệu là nhỏ nhất?
| $3$m |
| $1{,}5$m |
| $2$m |
| $1$m |
Một tấm bìa hình vuông có cạnh $44$cm, người ta cắt bỏ đi ở mỗi góc tấm bìa một hình vuông cạnh $12$cm rồi gấp lại thành một cái hộp chữ nhật không có nắp. Tính thể tích cái hộp này.
| $4800$cm$^3$ |
| $9600$cm$^3$ |
| $2400$cm$^3$ |
| $2400\sqrt{3}$cm$^3$ |
Tính thể tích của khối gỗ có hình dạng dưới đây
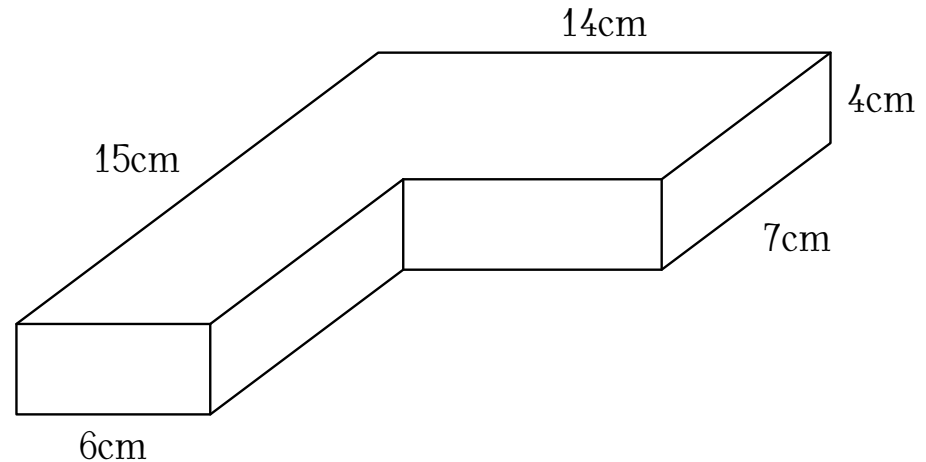
| $328$cm$^3$ |
| $456$cm$^3$ |
| $584$cm$^3$ |
| $712$cm$^3$ |
Một bể cá hình hộp chữ nhật có thể tích $0{,}36$m$^3$. Biết kích thước của đáy bể lần lượt bằng $0{,}5$m và $1{,}2$m. Chiều cao của bể cá bằng
| $0{,}65$m |
| $0{,}6$m |
| $0{,}7$m |
| $0{,}5$m |
Tính thể tích khối rubic lập phương có cạnh bằng $8$cm (Bỏ các khe hở của khối rubic, xem thể tích của khe hở không đáng kể).
| $24\,\mathrm{cm}^3$ |
| $8\,\mathrm{cm}^3$ |
| $512\,\mathrm{cm}^3$ |
| $\dfrac{512}{3}\,\mathrm{cm}^3$ |
Một viên gạch dạng khối hộp chữ nhật có ba kích thước là $3$cm, $10$cm, $20$cm. Tính thể tích viên gạch đó.
| $300$cm$^3$ |
| $200$cm$^3$ |
| $600$cm$^3$ |
| $1200$cm$^3$ |
Một lớp học có $16$ học sinh học giỏi môn Toán; $12$ học sinh học giỏi môn Văn; $8$ học sinh vừa học giỏi môn Toán và Văn; $19$ học sinh không học giỏi cả hai môn Toán và Văn. Hỏi lớp học có bao nhiêu học sinh?
| $31$ |
| $39$ |
| $47$ |
| $54$ |
Một chất điểm chuyển động theo phương trình \(s=-t^3+3t^2-2\), trong đó \(t\) tính bằng giây và \(s\) tính bằng mét. Tính vận tốc của chuyển động tại thời điểm gia tốc bị triệt tiêu.
| \(3\)m/s |
| \(2\)m/s |
| \(1\)m/s |
| \(0\)m/s |