Cho tứ diện \(ABCD\). Gọi \(M,\,N\) lần lượt là trung điểm của các cạnh \(AD\) và \(BC\); \(G\) là trọng tâm tam giác \(BCD\).

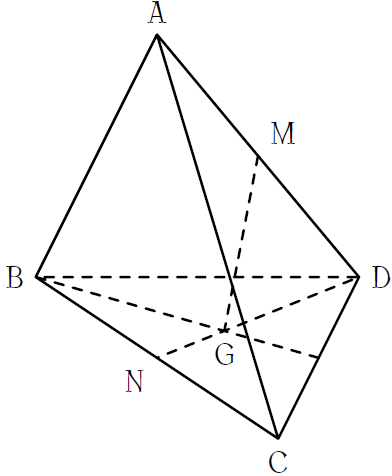
Khi ấy giao điểm của đường thẳng \(MG\) và mặt phẳng \((ABC)\) là

	Điểm \(C\)
	Điểm \(N\)
	Giao điểm của đường thẳng \(MG\) và đường thẳng \(BC\)
	Giao điểm của đường thẳng \(MG\) và đường thẳng \(AN\)

Tìm mệnh đề đúng trong các mệnh đề sau:

	Nếu hai mặt phẳng (\(\alpha\)) và (\(\beta\)) song song với nhau thì mọi đường thẳng nằm trong (\(\alpha\)) đều song song với mọi đường thẳng nằm trong (\(\beta\))
	Nếu hai đường thẳng song song với nhau lần lượt nằm trong hai mặt phẳng phân biệt (\(\alpha\)) và (\(\beta\)) thì (\(\alpha\)) và (\(\beta\)) song song với nhau
	Nếu hai mặt phẳng (\(\alpha\)) và (\(\beta\)) song song với nhau thì mọi đường thẳng nằm trong (\(\alpha\)) đều song song với (\(\beta\))
	Qua một điểm nằm ngoài mặt phẳng cho trước ta sẽ được một và chỉ một đường thẳng song song với mặt phẳng cho trước đó

Tìm mệnh đề sai trong các mệnh đề sau đây:

	Nếu hai mặt phẳng phân biệt cùng song song với một mặt phẳng thứ ba thì chúng song song với nhau
	Nếu hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau
	Nếu hai mặt phẳng có một điểm chung thì còn có vô số điểm chung khác nữa
	Nếu một đường thẳng cắt một trong hai mặt phẳng song song với nhau thì sẽ cắt mặt phẳng còn lại