Giá trị nhỏ nhất \(m\) của hàm số \(y=x^3-3x+5\) trên đoạn \([2;4]\) là
| \(0\) | |
| \(5\) | |
| \(7\) | |
| \(3\) |
Tìm giá trị nhỏ nhất của hàm số \(y=\dfrac{x+3}{2x-3}\) trên đoạn \([2;5]\).
| \(\dfrac{7}{8}\) | |
| \(\dfrac{8}{7}\) | |
| \(5\) | |
| \(\dfrac{2}{7}\) |
Tìm giá trị nhỏ nhất của hàm số \(y=\dfrac{x+1}{x-1}\) trên đoạn \([2;3]\).
| \(-3\) | |
| \(3\) | |
| \(2\) | |
| \(4\) |
Tìm giá trị lớn nhất của hàm số \(y=\dfrac{3x-1}{x-3}\) trên đoạn \([0;2]\).
| \(-\dfrac{1}{3}\) | |
| \(-5\) | |
| \(5\) | |
| \(\dfrac{1}{3}\) |
Hàm số nào sau đây không có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn \([-2;2]\).
| \(y=\dfrac{x-1}{x+1}\) | |
| \(y=x^2\) | |
| \(y=1-x\) | |
| \(y=x^3+2\) |
Tìm giá trị lớn nhất của hàm số $$y=3+\sqrt{x^2-2x+8}$$trên đoạn \([-2;2]\).
| \(7\) | |
| \(9\) | |
| \(3+2\sqrt{2}\) | |
| \(3+\sqrt{7}\) |
Tìm giá trị nhỏ nhất của hàm số \(y=x+1+\dfrac{4}{x}\) trên đoạn \([1;3]\).
| \(4\) | |
| \(\dfrac{16}{3}\) | |
| \(5\) | |
| \(6\) |
Giá trị lớn nhất của hàm số \(y=\dfrac{x^2-3x}{x+1}\) trên đoạn \([0;3]\) bằng
| \(3\) | |
| \(2\) | |
| \(0\) | |
| \(1\) |
Tìm giá trị lớn nhất của hàm số \(y=x^4-2x^2\) trên đoạn \([0;1]\).
| \(-1\) | |
| \(0\) | |
| \(1\) | |
| \(-2\) |
Giá trị lớn nhất của hàm số \(y=x^4-3x^2+2\) trên đoạn \([0;3]\) là
| \(57\) | |
| \(55\) | |
| \(56\) | |
| \(54\) |
Giá trị lớn nhất của hàm số \(y=x(5-2x)^2\) trên đoạn \([0;3]\) là
| \(\dfrac{250}{3}\) | |
| \(0\) | |
| \(\dfrac{250}{27}\) | |
| \(\dfrac{125}{27}\) |
Tìm giá trị lớn nhất của hàm số \(f(x)=x^3-5x^2+3x-1\) trên đoạn \([2;4]\).
| \(\max\limits_{[2;4]}f(x)=-5\) | |
| \(\max\limits_{[2;4]}f(x)=-10\) | |
| \(\max\limits_{[2;4]}f(x)=-7\) | |
| \(\max\limits_{[2;4]}f(x)=1\) |
Tìm giá trị lớn nhất của hàm số \(f(x)=2x^3+3x^2-12x+2\) trên đoạn \([-1;2]\).
| \(\max\limits_{[-1;2]}f(x)=10\) | |
| \(\max\limits_{[-1;2]}f(x)=6\) | |
| \(\max\limits_{[-1;2]}f(x)=11\) | |
| \(\max\limits_{[-1;2]}f(x)=15\) |
Tìm giá trị lớn nhất của hàm số \(f(x)=x^3-8x^2+16x-9\) trên đoạn \([1;3]\).
| \(\max\limits_{[1;3]}f(x)=5\) | |
| \(\max\limits_{[1;3]}f(x)=\dfrac{13}{27}\) | |
| \(\max\limits_{[1;3]}f(x)=-6\) | |
| \(\max\limits_{[1;3]}f(x)=0\) |
Giá trị lớn nhất của hàm số \(y=x^3-3x+4\) trên đoạn \([-2;2]\) là
| \(10\) | |
| \(6\) | |
| \(24\) | |
| \(4\) |
Giá trị nhỏ nhất của hàm số \(y=x^3-3x+5\) trên đoạn \([2;4]\) là
| \(3\) | |
| \(7\) | |
| \(5\) | |
| \(0\) |
Cho bảng biến thiên của hàm số \(y=f(x)\) như hình.
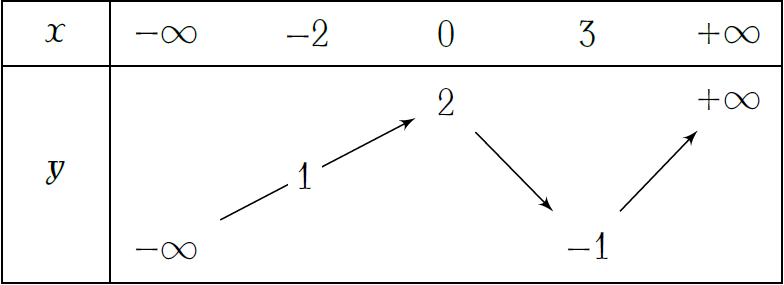
Tìm giá trị lớn nhất \(M\) và giá trị nhỏ nhất \(m\) của hàm số trên đoạn \([-2;3]\).
| \(\begin{cases}M=3\\ m=-2\end{cases}\) | |
| \(\begin{cases}M=0\\ m=3\end{cases}\) | |
| \(\begin{cases}M=2\\ m=-1\end{cases}\) | |
| \(\begin{cases}M=1\\ m=-1\end{cases}\) |
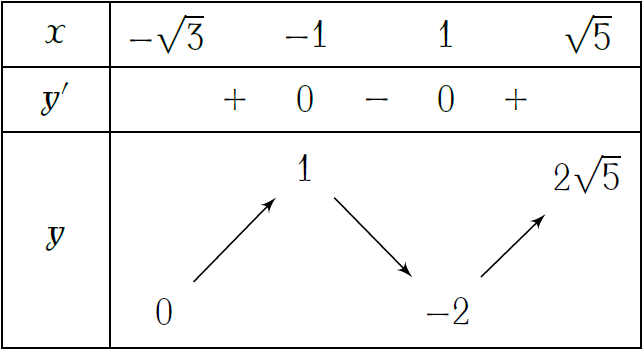
Cho hàm số \(y=f(x)\) xác định trên đoạn \(\left[-\sqrt{3};\sqrt{5}\right]\) và có bảng biến thiên như hình vẽ. Khẳng định nào sau đây là đúng?
| \(\min\limits_{\left[-\sqrt{3};\sqrt{5}\right]}f(x)=0\) | |
| \(\max\limits_{\left[-\sqrt{3};\sqrt{5}\right]}f(x)=2\) | |
| \(\max\limits_{\left[-\sqrt{3};\sqrt{5}\right]}f(x)=2\sqrt{5}\) | |
| \(\min\limits_{\left[-\sqrt{3};\sqrt{5}\right]}f(x)=2\) |
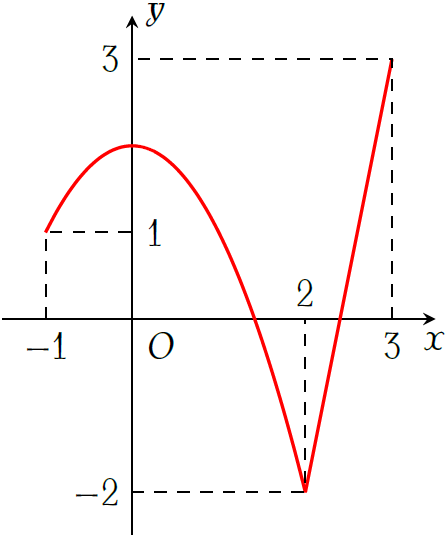
Cho hàm số \(y=f(x)\) liên tục trên đoạn \([-1;3]\) và có đồ thị như hình vẽ. Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn \([-1;3]\). Giá trị của \(M-m\) bằng
| \(0\) | |
| \(1\) | |
| \(4\) | |
| \(5\) |
Đồ thị hàm số \(y=x^3-2mx^2+m^2x+n\) có tọa độ điểm cực tiểu là \((1;3)\). Khi đó \(m+n\) bằng
| \(4\) | |
| \(3\) | |
| \(2\) | |
| \(1\) |
