Biết rằng \(\displaystyle\int\limits_{1}^{5}\dfrac{1}{2x-1}\mathrm{\,d}x=\ln a\). Giá trị của \(a\) là
| \(81\) | |
| \(27\) | |
| \(3\) | |
| \(9\) |
Tính \(I=\displaystyle\int\limits_{\mathrm{e}}^{\mathrm{e}^2}\dfrac{\left(1-\ln x\right)^2}{x}\mathrm{\,d}x\) được kết quả là
| \(\dfrac{4}{3}\) | |
| \(\dfrac{5}{3}\) | |
| \(\dfrac{1}{3}\) | |
| \(\dfrac{13}{3}\) |
Tính tích phân \(I=\displaystyle\int\limits_{0}^{2}(x+2)^3\mathrm{\,d}x\).
| \(I=60\) | |
| \(I=240\) | |
| \(I=56\) | |
| \(I=120\) |
Nếu \(\displaystyle\int\limits_{0}^{3}\dfrac{x}{1+\sqrt{1+x}}\mathrm{\,d}x=\displaystyle\int\limits_{1}^{2}f(t)\mathrm{\,d}t\), với \(t=\sqrt{1+x}\) thì \(f(t)\) là hàm số nào trong các hàm số dưới đây?
| \(f(t)=t^2-1\) | |
| \(f(t)=2t^2+2t\) | |
| \(f(t)=t^2+t\) | |
| \(f(t)=2t^2-2t\) |
Cho hàm số \(y=f(x)\) liên tục trên đoạn \([a;b]\). Mệnh đề nào dưới đây sai?
| \(\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x=-\displaystyle\int\limits_{b}^{a}f(x)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_{a}^{b}k\mathrm{\,d}x=k(a-b),\,\forall k\in\mathbb{R}\) | |
| \(\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x=\displaystyle\int\limits_{a}^{c}f(x)\mathrm{\,d}x+\displaystyle\int\limits_{c}^{b}f(x)\mathrm{\,d}x,\,\forall c\in(a;b)\) | |
| \(\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x=\displaystyle\int\limits_{a}^{b}f(t)\mathrm{\,d}t\) |
Cho hàm số \(y=f(x)\) có đạo hàm trên đoạn \([-2;1]\) và \(f(-2)=3\), \(f(1)=7\). Tính \(I=\displaystyle\int\limits_{-2}^{1}f'(x)\mathrm{\,d}x\).
| \(I=\dfrac{7}{3}\) | |
| \(I=-4\) | |
| \(I=10\) | |
| \(I=4\) |
Biết \(\displaystyle\int(x+3)\cdot\mathrm{e}^{-3x+1}\mathrm{\,d}x=-\dfrac{1}{m}\mathrm{e}^{-3x+1}(3x+n)+C\) với \(m,\,n\) là các số nguyên. Tính tổng \(S=m+n\).
| \(10\) | |
| \(1\) | |
| \(9\) | |
| \(19\) |
Biết \(F(x)\) là nguyên hàm của hàm số \(f(x)=\dfrac{1}{x-1}\) và \(F(2)=1\). Khi đó \(F(3)\) bằng bao nhiêu?
| \(\ln\dfrac{3}{2}\) | |
| \(\ln2+1\) | |
| \(\ln2\) | |
| \(\dfrac{1}{2}\) |
Phát biểu nào sau đây là đúng?
| \(\displaystyle\int x\sin x\mathrm{\,d}x=x\cos x+\sin x+C\) | |
| \(\displaystyle\int x\sin x\mathrm{\,d}x=-x\cos x+\sin x+C\) | |
| \(\displaystyle\int x\sin x\mathrm{\,d}x=-x\cos x-\sin x+C\) | |
| \(\displaystyle\int x\sin x\mathrm{\,d}x=x\cos x-\sin x+C\) |
Cặp số nào sau đây có tính chất "Có một hàm số là nguyên hàm của hàm số còn lại"?
| \(\tan x^2\) và \(\dfrac{1}{\cos^2x^2}\) | |
| \(\sin2x\) và \(\sin^2x\) | |
| \(\mathrm{e}^x\) và \(\mathrm{e}^{-x}\) | |
| \(\sin2x\) và \(\cos^2x\) |
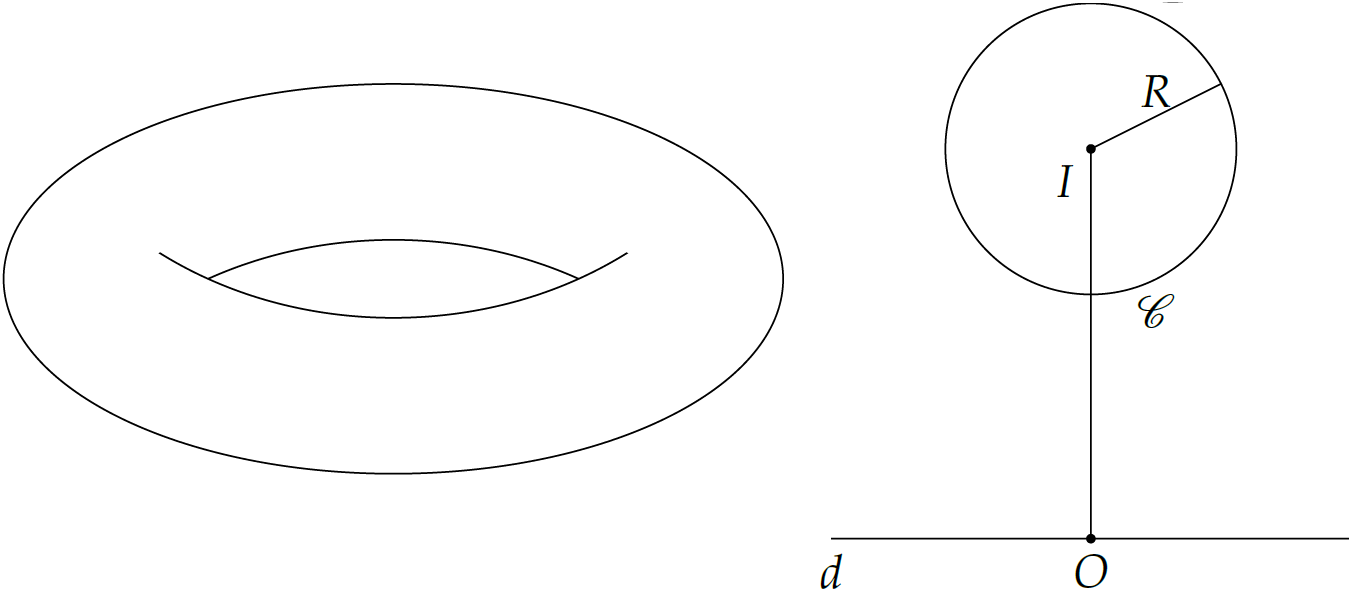
Người ta làm một chiếc phao bơi như hình vẽ (với bề mặt có được bằng cách quay đường tròn \(\mathscr{C}\) quanh trục \(d\)). Biết rằng \(OI=30\)cm, \(R=5\)cm. Tính thể tích \(V\) của chiếc phao.
| \(V=1500\pi^2\text{cm}^3\) | |
| \(V=9000\pi^2\text{cm}^3\) | |
| \(V=1500\pi\text{cm}^3\) | |
| \(V=9000\pi\text{cm}^3\) |
Thể tích của khối tròn xoay sinh ra khi cho hình phẳng giới hạn bởi parabol \((P)\colon y=x^2\) và đường thẳng \(d\colon y=x\) xoay quanh trục \(Ox\) bằng
| \(\pi\displaystyle\int\limits_{0}^{1}x^2\mathrm{\,d}x-\pi\displaystyle\int\limits_{0}^{1}x^4\mathrm{\,d}x\) | |
| \(\pi\displaystyle\int\limits_{0}^{1}x^2\mathrm{\,d}x+\pi\displaystyle\int\limits_{0}^{1}x^4\mathrm{\,d}x\) | |
| \(\pi\displaystyle\int\limits_{0}^{1}\left(x^2-x\right)^2\mathrm{\,d}x\) | |
| \(\pi\displaystyle\int\limits_{0}^{1}\left(x^2-x\right)\mathrm{\,d}x\) |
Thể tích khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi đồ thị các hàm số \(y=x^2-2x\), \(y=0\), \(x=-1\), \(x=2\) quanh trục \(Ox\) bằng
| \(\dfrac{16\pi}{5}\) | |
| \(\dfrac{17\pi}{5}\) | |
| \(\dfrac{18\pi}{5}\) | |
| \(\dfrac{5\pi}{18}\) |
Tính diện tích \(S\) của hình phẳng giới hạn bởi đồ thị các hàm số \(y=|x|\) và \(y=x^2-2\).
| \(S=\dfrac{20}{3}\) | |
| \(S=\dfrac{11}{2}\) | |
| \(S=3\) | |
| \(S=\dfrac{13}{3}\) |
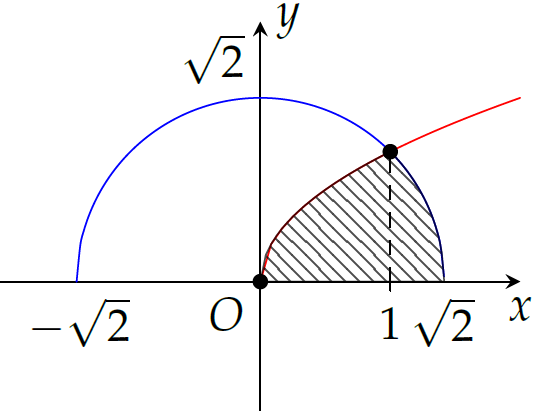
Cho \((H)\) là hình phẳng giới hạn bởi đường cong có phương trình \(y=\sqrt{x}\), nửa đường tròn có phương trình \(y=\sqrt{2-x^2}\) (với \(0\leq x\leq\sqrt{2}\)) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của \((H)\) bằng
| \(\dfrac{3\pi+2}{12}\) | |
| \(\dfrac{4\pi+2}{12}\) | |
| \(\dfrac{3\pi+1}{12}\) | |
| \(\dfrac{4\pi+1}{6}\) |
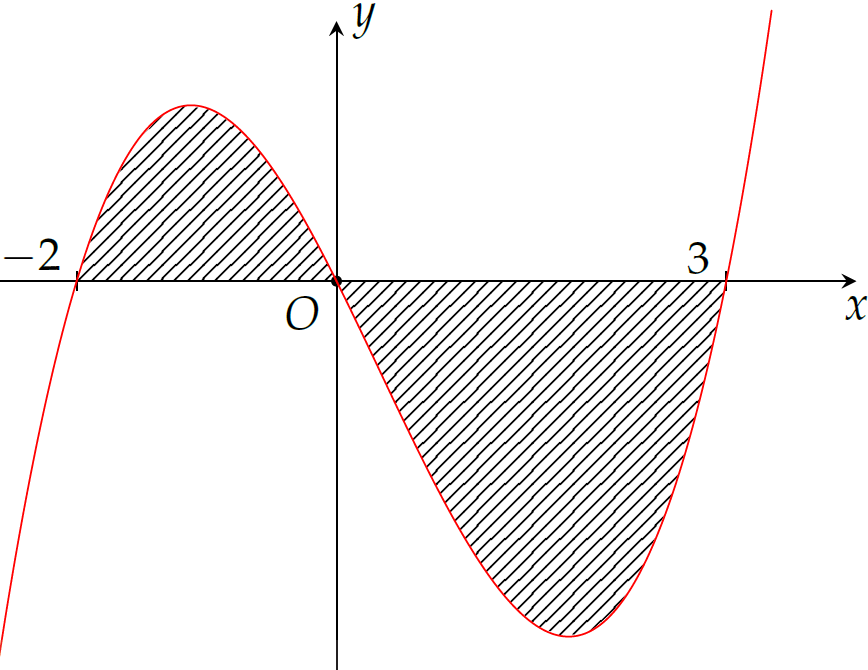
Cho đồ thị hàm số \(y=f(x)\) như hình vẽ và \(\displaystyle\int\limits_{-2}^{0}f(x)\mathrm{\,d}x=a\), \(\displaystyle\int\limits_{0}^{3}f(x)\mathrm{\,d}x=b\). Tính diện tích của phần được gạch chéo theo \(a\) và \(b\).
| \(\dfrac{a+b}{2}\) | |
| \(a-b\) | |
| \(b-a\) | |
| \(a+b\) |
Cho hàm số \(f(x)\) liên tục trên đoạn \([a;b]\). Diện tích hình phẳng giới hạn bởi đường cong \(y=f(x)\), trục hoành, các đường thẳng \(x=a\), \(x=b\) là
| \(\displaystyle\int\limits_{b}^{a}f(x)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_{a}^{b}\left|f(x)\right|\mathrm{\,d}x\) | |
| \(-\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x\) |
Một ô tô đang đi với vận tốc lớn hơn \(72\)km/h, phía trước là đoạn đường chỉ cho phép chạy với tốc độ tối đa là \(72\)km/h, vì thế người lái xe đạp phanh để ô tô chuyển động chậm dần đều với vận tốc \(v(t)=30-2t\) (m/s), trong đó \(t\) là khoảng thời gian tính bằng giây kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc bắt đầu đạp phanh đến lúc đạt tốc độ \(72\)km/h, ô tô đã di chuyển quãng đường là bao nhiêu mét?
| \(100\)m | |
| \(150\)m | |
| \(175\)m | |
| \(125\)m |
Giá trị nào của \(a\) để $$\displaystyle\int\limits_{0}^{a}\left(3x^2+2\right)\mathrm{\,d}x=a^3+2?$$
| \(1\) | |
| \(2\) | |
| \(0\) | |
| \(3\) |
Cho \(I=\displaystyle\int\limits_{1}^{2}x\sqrt{4-x^2}\mathrm{\,d}x\) và \(t=\sqrt{4-x^2}\). Khẳng định nào sau đây sai?
| \(I=\sqrt{3}\) | |
| \(I=\dfrac{t^2}{2}\bigg|_0^{\sqrt{3}}\) | |
| \(I=\displaystyle\int\limits_{0}^{\sqrt{3}}t^2\mathrm{\,d}t\) | |
| \(I=\dfrac{t^3}{3}\bigg|_0^{\sqrt{3}}\) |
