Có tất cả bao nhiêu khối đa diện đều?

	\(7\)
	\(6\)
	\(5\)
	\(4\)

Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng?

	\(5\)
	\(4\)
	\(3\)
	\(2\)

Cho khối lăng trụ \(ABC.A'B'C'\) có đáy là tam giác vuông tại \(B\), biết \(AB=a\), \(BC=a\sqrt{3}\) và thể tích của khối lăng trụ bằng \(\dfrac{a^3\sqrt{6}}{2}\). Chiều cao của lăng trụ là

	\(\dfrac{a\sqrt{3}}{2}\)
	\(a\sqrt{3}\)
	\(\dfrac{a\sqrt{2}}{2}\)
	\(a\sqrt{2}\)

Khối bát diện đều có bao nhiêu cạnh?

	\(10\)
	\(9\)
	\(8\)
	\(12\)

Phương trình \(4^{x^2-x}+2^{x^2-x+1}=3\) có nghiệm là

	\(\left[\begin{array}{l}x=0\\ x=2\end{array}\right.\)
	\(\left[\begin{array}{l}x=-1\\ x=1\end{array}\right.\)
	\(\left[\begin{array}{l}x=0\\ x=1\end{array}\right.\)
	\(\left[\begin{array}{l}x=1\\ x=2\end{array}\right.\)

Hàm số nào sau đây đồng biến trên \(\mathbb{R}\)?

	\(y=\dfrac{x-1}{x+1}\)
	\(y=\log_2x\)
	\(y=3^x\)
	\(y=x^4+2x^2+4\)

Tìm đạo hàm của hàm số \(y=\log_2(2x+1)\).

	\(y'=\dfrac{1}{2x+1}\)
	\(y'=\dfrac{1}{(2x+1)\ln2}\)
	\(y'=\dfrac{2}{(2x+1)\ln2}\)
	\(y'=\dfrac{2}{2x+1}\)

Tìm tất cả giá trị của tham số \(m\) để hàm số $$y=x^3+2x^2-mx+1$$đồng biến trên \(\mathbb{R}\).

	\(m\leq-\dfrac{4}{3}\)
	\(m\geq-\dfrac{4}{3}\)
	\(m<-\dfrac{4}{3}\)
	\(m>-\dfrac{4}{3}\)

Tập hợp các giá trị \(m\) để đồ thị hàm số \(y=\dfrac{mx^2+6x-2}{x+2}\) có tiệm cận đứng là

	\(\left\{\dfrac{7}{2}\right\}\)
	\(\mathbb{R}\setminus\left\{-\dfrac{7}{2}\right\}\)
	\(\mathbb{R}\)
	\(\mathbb{R}\setminus\left\{\dfrac{7}{2}\right\}\)

Điểm cực tiểu của đồ thị hàm số \(y=-x^3+x^2+5x-5\) là điểm nào?

	\((-1;-8)\)
	\((1;0)\)
	\((0;-5)\)
	\(\left(\dfrac{5}{3};\dfrac{40}{27}\right)\)

Đồ thị sau đây là của hàm số \(y=x^3-3x+1\).

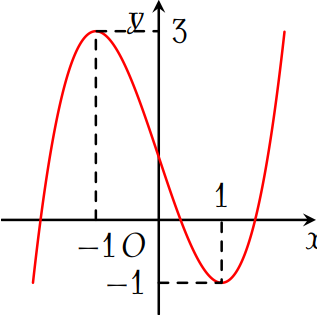
Với giá trị nào của \(m\) thì phương trình \(x^3-3x-m=0\) có \(3\) nghiệm phân biệt?

	\(-2< m<2\)
	\(-2< m<3\)
	\(-1< m<3\)
	\(-2\leq m<2\)

Cho khối lăng trụ \(ABC.A'B'C'\) có thể tích bằng \(a^3\). Gọi \(M,\,N\) lần lượt là trung điểm của \(A'B'\) và \(CC'\). Tính thể tích khối chóp \(ABMN\).

	\(\dfrac{2a^3}{3}\)
	\(\dfrac{a^3}{3}\)
	\(\dfrac{a^3\sqrt{3}}{2}\)
	\(a^3\sqrt{3}\)

Lăng trụ tam giác \(ABC.A'B'C'\) có thể tích bằng \(V\). Khi đó thể tích khối chóp \(A.BCC'B'\) bằng

	\(\dfrac{V}{3}\)
	\(\dfrac{2V}{3}\)
	\(\dfrac{3V}{4}\)
	\(\dfrac{V}{2}\)

Hãy chọn mệnh đề đúng.

	Số đỉnh và số mặt trong một hình đa diện luôn bằng nhau
	Tồn tại hình đa diện có số đỉnh bằng số cạnh
	Tồn tại hình đa diện có số đỉnh và số mặt bằng nhau
	Tồn tại hình đa diện có số cạnh bằng số mặt

Cho hàm số \(y=f(x)\) có đạo hàm trên khoảng \(\mathbb{K}\). Mệnh đề nào dưới đây đúng?

	Nếu \(f'(x)\geq0\) với mọi \(x\) thuộc \(\mathbb{K}\) thì hàm số \(f(x)\) đồng biến trên \(\mathbb{K}\)
	Nếu \(f'(x)\leq0\) với mọi \(x\) thuộc \(\mathbb{K}\) thì hàm số \(f(x)\) đồng biến trên \(\mathbb{K}\)
	Nếu \(f'(x)<0\) với mọi \(x\) thuộc \(\mathbb{K}\) thì hàm số \(f(x)\) đồng biến trên \(\mathbb{K}\)
	Nếu \(f'(x)>0\) với mọi \(x\) thuộc \(\mathbb{K}\) thì hàm số \(f(x)\) đồng biến trên \(\mathbb{K}\)

Biết rằng đường thẳng \(y=4x+5\) cắt đồ thị hàm số \(y=x^3+2x+1\) tại điểm duy nhất, kí hiệu \(\left(x_0;y_0\right)\) là tọa độ của điểm đó. Tìm \(y_0\).

	\(y_0=11\)
	\(y_0=10\)
	\(y_0=13\)
	\(y_0=12\)

Hàm số \(y=f(x)\) liên tục trên đoạn \([-1;3]\) và có bảng biến thiên như sau:

Gọi \(M\) là giá trị lớn nhất của hàm số \(y=f(x)\) trên đoạn \([-1;3]\). Khẳng định nào sau đây là khẳng định đúng?

	\(M=f(0)\)
	\(M=f(3)\)
	\(M=f(2)\)
	\(M=f(-1)\)

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\). Biết cạnh bên \(SA=2a\) và vuông góc với mặt đáy. Tính thể tích khối chóp \(S.ABCD\).

	\(\dfrac{2a^3}{3}\)
	\(2a^3\)
	\(\dfrac{4a^3}{3}\)
	\(\dfrac{a^3}{3}\)

Một khối hộp chữ nhật có bao nhiêu đỉnh?

	\(6\)
	\(10\)
	\(8\)
	\(12\)

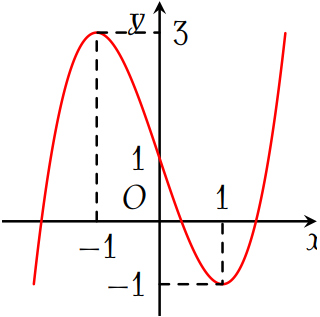
Đường cong trong hình vẽ là đồ của hàm số nào dưới đây?

	\(y=x^3-3x+3\)
	\(y=x^3-3x\)
	\(y=x^3-3x+1\)
	\(y=-x^3+3x+1\)