Xác định parabol $\left(\mathscr{P}\right)\colon y=ax^2+bx+c$, biết rằng $\left(\mathscr{P}\right)$ đi qua ba điểm $A(1;1)$, $B(-1;-3)$ và $O(0;0)$.

	$y=x^2+2x$
	$y=-x^2-2x$
	$y=-x^2+2x$
	$y=x^2-2x$

Xác định parabol $\left(\mathscr{P}\right)\colon y=2x^2+bx+c$, biết rằng $\left(\mathscr{P}\right)$ đi qua điểm $M(0;4)$ và có trục đối xứng $x=1$.

	$y=2x^2-4x+4$
	$y=2x^2+4x-3$
	$y=2x^2-3x+4$
	$y=x^2-2x+3$

Xác định parabol $\left(\mathscr{P}\right)\colon y=2x^2+bx+c$, biết rằng $\left(\mathscr{P}\right)$ có đỉnh $I(-1;-2)$.

	$y=2x^2-4x+4$
	$y=2x^2-4x$
	$y=2x^2-3x+4$
	$y=2x^2+4x$

Xác định parabol $\left(\mathscr{P}\right)\colon y=ax^2+bx+2$, biết rằng $\left(\mathscr{P}\right)$ đi qua điểm $M(1;5)$ và $N(-2;8)$.

	$y=2x^2+x+2$
	$y=x^2+x+2$
	$y=-2x^2+x+2$
	$y=-2x^2-x+2$

Hàm số nào sau đây đạt giá trị nhỏ nhất tại $x=\dfrac{3}{4}$?

	$y=4x^2-3x+1$
	$y=-x^2+\dfrac{3}{2}x+1$
	$y=-2x^2+3x+1$
	$y=x^2-\dfrac{3}{2}x+1$

Tìm giá trị nhỏ nhất $m$ của hàm số $y=x^2-4x+5$.

	$m=0$
	$m=-2$
	$m=2$
	$m=1$

Hàm số nào sau đây có đồ thị là parabol có đỉnh $I(-1;3)$?

	$y=2x^2-4x-3$
	$y=2x^2-2x-1$
	$y=2x^2+4x+5$
	$y=2x^2+x+2$

Parabol $\left(\mathscr{P}\right)\colon y=3x^2-2x+1$ có đỉnh là

	$A\left(-\dfrac{1}{3};\dfrac{2}{3}\right)$
	$B\left(-\dfrac{1}{3};-\dfrac{2}{3}\right)$
	$C\left(\dfrac{1}{3};-\dfrac{2}{3}\right)$
	$D\left(\dfrac{1}{3};\dfrac{2}{3}\right)$

Trong các hàm số sau, hàm số nào có đồ thị nhận đường thẳng $x=1$ làm trục đối xứng?

	$y=-2x^2+4x+1$
	$y=2x^2+4x-3$
	$y=2x^2-2x-1$
	$y=x^2-x+2$

Trục đối xứng của parabol $\left(\mathscr{P}\right)\colon y=2x^2+6x+3$ là

	$x=-\dfrac{3}{2}$
	$y=-\dfrac{3}{2}$
	$x=-3$
	$y=-3$

Cho hàm số $y=ax^2+bx+c$ $(a\neq0)$ có đồ thị $\left(\mathscr{P}\right)$. Tọa độ đỉnh của $\left(\mathscr{P}\right)$ là

	$I\left(-\dfrac{b}{2a};\dfrac{\Delta}{4a}\right)$
	$I\left(-\dfrac{b}{a};-\dfrac{\Delta}{4a}\right)$
	$I\left(-\dfrac{b}{2a};-\dfrac{\Delta}{4a}\right)$
	$I\left(\dfrac{b}{2a};\dfrac{\Delta}{4a}\right)$

Các kích thước của một bể bơi được cho trên hình vẽ (mặt nước có dạng hình chữ nhật).

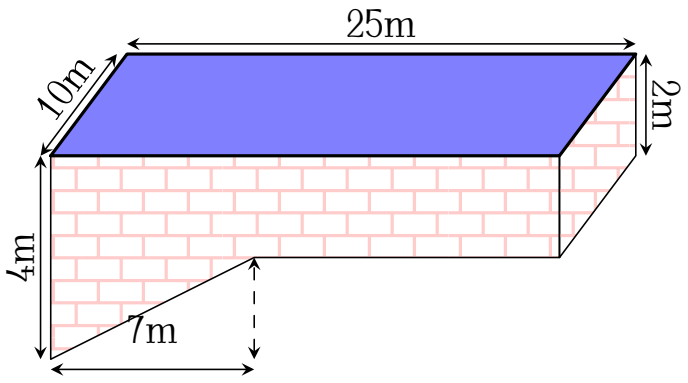
Hãy tính xem bể bơi chứa được bao nhiêu mét khối nước khi nó đầy ắp nước?

	$1000$m$^3$
	$640$m$^3$
	$570$m$^3$
	$500$m$^3$

Một người bán gạo muốn đóng một thùng tôn đựng gạo có thể tích không đổi bằng $8$m$^3$, thùng tôn hình hộp chữ nhật có đáy là hình vuông, không nắp. Trên thị trường, giá tôn làm đáy thùng là $100.000$ đồng/m$^2$, giá tôn làm thành xung quanh thùng là $50.000$ đồng/m$^2$. Hỏi người bán gạo đó cần đóng thùng đựng gạo với cạnh đáy bằng bao nhiêu để chi phí mua nguyên liệu là nhỏ nhất?

	$3$m
	$1{,}5$m
	$2$m
	$1$m

Một tấm bìa hình vuông có cạnh $44$cm, người ta cắt bỏ đi ở mỗi góc tấm bìa một hình vuông cạnh $12$cm rồi gấp lại thành một cái hộp chữ nhật không có nắp. Tính thể tích cái hộp này.

	$4800$cm$^3$
	$9600$cm$^3$
	$2400$cm$^3$
	$2400\sqrt{3}$cm$^3$

Tính thể tích của khối gỗ có hình dạng dưới đây

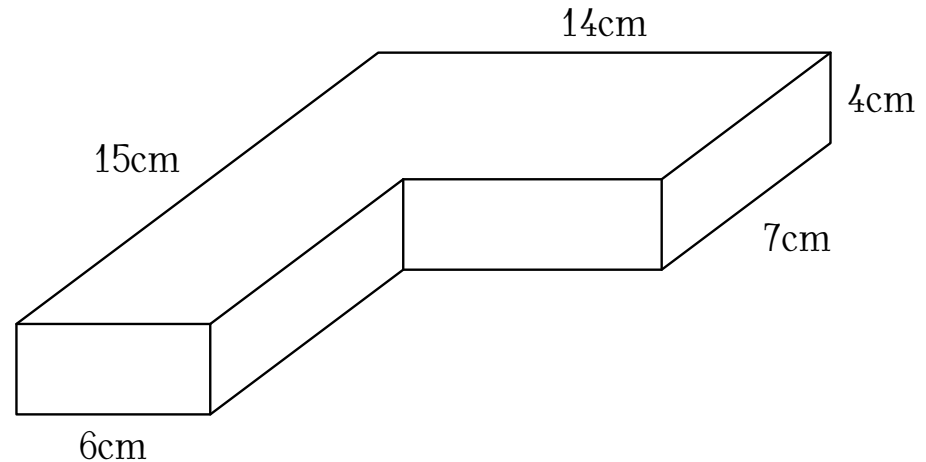
	$328$cm$^3$
	$456$cm$^3$
	$584$cm$^3$
	$712$cm$^3$

Một bể cá hình hộp chữ nhật có thể tích $0{,}36$m$^3$. Biết kích thước của đáy bể lần lượt bằng $0{,}5$m và $1{,}2$m. Chiều cao của bể cá bằng

	$0{,}65$m
	$0{,}6$m
	$0{,}7$m
	$0{,}5$m

Cho khối lăng trụ $ABC.A'B'C'$ có thể tích bằng $V$. Thể tích của khối đa diện $ABCC'B'$ bằng

	$\dfrac{3V}{4}$
	$\dfrac{2V}{3}$
	$\dfrac{V}{2}$
	$\dfrac{V}{4}$

Cho khối chóp $S.ABCD$ có đáy là hình bình hành và có thể tích $48$. Trên các cạnh $SA,\,SB,\,SC,\,SD$ lần lượt lấy các điểm $A',\,B',\,C'$ và $D'$ sao cho $\dfrac{SA'}{SA}=\dfrac{SC'}{SC}=\dfrac{1}{3}$ và $\dfrac{SB'}{SB}=\dfrac{SD'}{SD}=\dfrac{3}{4}$. Tính thể tích $V$ của khối đa diện lõm $S.A'B'C'D'$.

	$V=4$
	$V=9$
	$V=\dfrac{3}{2}$
	$V=6$

Cho tứ diện $ABCD$. Các điểm $M$, $N$, $P$ lần lượt thuộc các cạnh $AB$, $AC$, $AD$ sao cho $MA=MB$, $NA=2NC$, $PA=3PD$. Biết thể tích khối tứ diện $AMNP$ bằng $V$ thì khối tứ diện $ABCD$ tính theo $V$ có giá trị là

	$4V$
	$6V$
	$12V$
	$8V$

Cho hình chóp $S.ABC$, gọi $M$, $N$ lần lượt là trung điểm của cạnh $SA$, $SB$. Tính tỉ số $\dfrac{\mathrm{V}_{S.ABC}}{\mathrm{V}_{S.MNC}}$.

	$4$
	$\dfrac{1}{2}$
	$2$
	$\dfrac{1}{4}$