Hàm số nào dưới đây đồng biến trên $\mathbb{R}$?
| $y=x^4-x^2$ | |
| $y=x^3-x$ | |
| $y=\dfrac{x-1}{x+2}$ | |
| $y=x^3+x$ |
Cho hàm số $f(x)=1-\dfrac{1}{\cos^22x}$. Khẳng định nào dưới đây đúng?
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=x+\tan2x+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=x+\dfrac{1}{2}\cot2x+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=x-\dfrac{1}{2}\tan2x+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=x+\dfrac{1}{2}\tan2x+C$ |
Cho hình hộp chữ nhật $ABCD.A'B'C'D'$ có $AB=a$, $BC=2a$ và $AA'=3a$ (tham khảo hình bên).
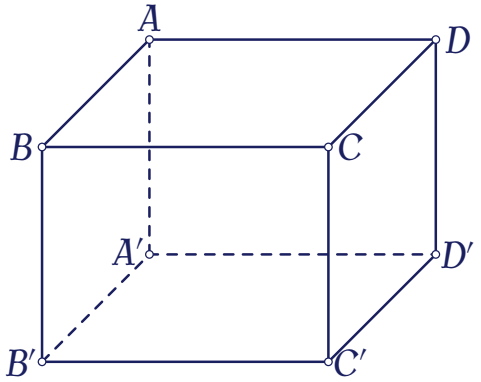
Khoảng cách giữa hai đường thẳng $BD$ và $A'C'$ bằng
| $a$ | |
| $a\sqrt{2}$ | |
| $2a$ | |
| $3a$ |
Cho hình lăng trụ đứng $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông tại $B$, $AC=2$, $AB=\sqrt{3}$ và $AA'=1$ (tham khảo hình bên).
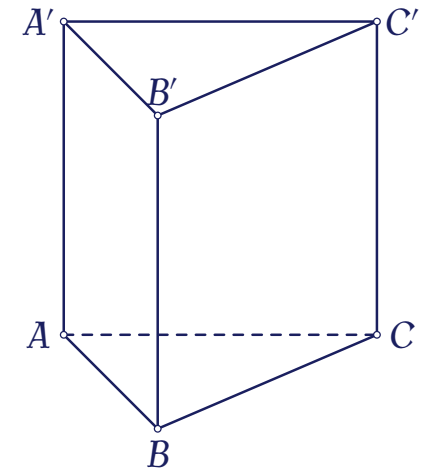
Góc giữa hai mặt phẳng $(ABC')$ và $(ABC)$ bằng
| $30^\circ$ | |
| $45^\circ$ | |
| $90^\circ$ | |
| $60^\circ$ |
Gọi $z_1$ và $z_2$ là hai nghiệm phức của phương trình $z^2+z+6=0$. Khi đó $z_1+z_2+z_1z_2$ bằng
| $7$ | |
| $5$ | |
| $-7$ | |
| $-5$ |
Có bao nhiêu số nguyên thuộc tập xác định của hàm số $y=\log\big[(6-x)(x+2)\big]$?
| $7$ | |
| $8$ | |
| $9$ | |
| Vô số |
Giá trị lớn nhất của hàm số $f(x)=x^3-3x^2-9x+10$ trên đoạn $[-2;2]$ bằng
| $-12$ | |
| $10$ | |
| $15$ | |
| $-1$ |
Trong không gian $Oxyz$, cho ba điểm $A(1;2;-1)$, $B(3;0;1)$ và $C(2;2;-2)$. Đường thẳng đi qua $A$ và vuông góc với mặt phẳng $(ABC)$ có phương trình là
| $\dfrac{x-1}{1}=\dfrac{y-2}{-2}=\dfrac{z+1}{3}$ | |
| $\dfrac{x+1}{1}=\dfrac{y+2}{2}=\dfrac{z-1}{1}$ | |
| $\dfrac{x-1}{1}=\dfrac{y-2}{2}=\dfrac{z-1}{-1}$ | |
| $\dfrac{x-1}{1}=\dfrac{y-2}{2}=\dfrac{z+1}{1}$ |
Đạo hàm của hàm số $y=x^{-3}$ là
| $y'=-x^{-4}$ | |
| $y'=-\dfrac{1}{2}x^{-2}$ | |
| $y'=-\dfrac{1}{3}x^{-4}$ | |
| $y'=-3x^{-4}$ |
Cho hàm số $f(x)=\mathrm{e}^x+2x$. Khẳng định nào dưới đây đúng?
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=\mathrm{e}^x+x^2+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=\mathrm{e}^x+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=\mathrm{e}^x-x^2+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=\mathrm{e}^x+2x^2+C$ |
Cho hai số phức $z_1=2+3i$ và $z_2=1-i$. Số phức $z_1+z_2$ bằng
| $5+i$ | |
| $3+2i$ | |
| $1+4i$ | |
| $3+4i$ |
Trên mặt phẳng tọa độ, điểm biểu diễn số phức $z=2-7i$ có tọa độ là
| $(2;7)$ | |
| $(-2;7)$ | |
| $(2;-7)$ | |
| $(-7;2)$ |
Cho tam giác $OIM$ vuông tại $I$ có $OI=3$ và $IM=4$. Khi quay tam giác $OIM$ quanh cạnh góc vuông $OI$ thì đường gấp khúc $OIM$ tạo thành hình nón có độ dài đường sinh bằng
| $7$ | |
| $3$ | |
| $5$ | |
| $4$ |
Trong không gian $Oxyz$, cho đường thẳng $d\colon\begin{cases}x=2+t\\ y=1-2t\\ z=-1+3t \end{cases}$. Vectơ nào dưới đây là một vectơ chỉ phương của $d$?
| $\overrightarrow{u_1}=(2;1;-1)$ | |
| $\overrightarrow{u_2}=(1;2;3)$ | |
| $\overrightarrow{u_3}=(1;-2;3)$ | |
| $\overrightarrow{u_4}=(2;1;1)$ |
Cho hàm số $y=ax^4+bx^2+c$ có đồ thị như đường cong trong hình bên.
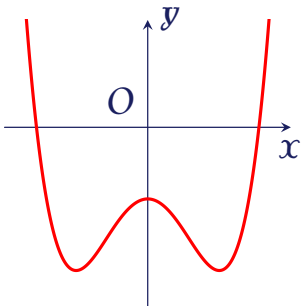
Số điểm cực trị của hàm số đã cho là
| $2$ | |
| $3$ | |
| $1$ | |
| $0$ |
Nghiệm của phương trình $3^{2x+1}=3^{2-x}$ là
| $x=\dfrac{1}{3}$ | |
| $x=0$ | |
| $x=-1$ | |
| $x=1$ |
Trong không gian $Oxyz$, phương trình của mặt phẳng $(Oyz)$ là
| $z=0$ | |
| $x=0$ | |
| $x+y+z=0$ | |
| $y=0$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
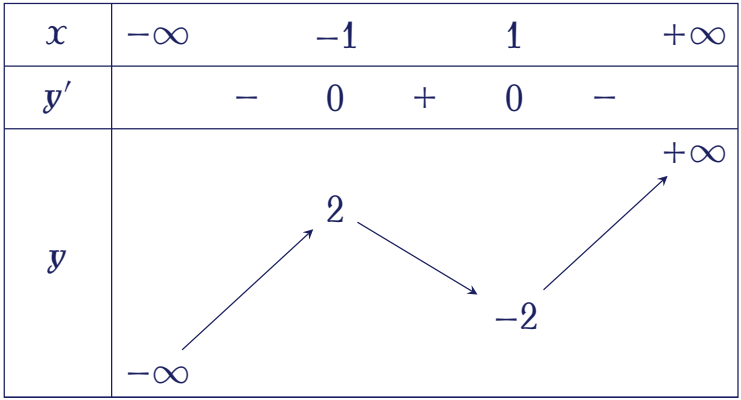
Điểm cực tiểu của hàm số đã cho là
| $x=-2$ | |
| $x=2$ | |
| $x=-1$ | |
| $x=1$ |
Số các tổ hợp chập $3$ của $12$ là
| $1320$ | |
| $36$ | |
| $220$ | |
| $1728$ |
Với $a$ là số thực dương tùy ý, $4\log\sqrt{a}$ bằng
| $-2\log a$ | |
| $2\log a$ | |
| $-4\log a$ | |
| $8\log a$ |
