Tìm số phức liên hợp của số phức $$z=1-3\mathrm{i}+(1-\mathrm{i})^2$$

	\(\overline{z}=-1-5\mathrm{i}\)
	\(\overline{z}=1-5\mathrm{i}\)
	\(\overline{z}=1+5\mathrm{i}\)
	\(\overline{z}=5-\mathrm{i}\)

Tìm số phức liên hợp của số phức $$z=(3+2\mathrm{i})(3-2\mathrm{i})$$

	\(\overline{z}=13\)
	\(\overline{z}=\mathrm{i}\)
	\(\overline{z}=0\)
	\(\overline{z}=-13\)

Cho số phức \(z=2-3\mathrm{i}\). Tìm phần ảo của số phức $$w=(1+\mathrm{i})z-(2-\mathrm{i})\overline{z}$$

	\(-5\)
	\(-9\)
	\(-5\mathrm{i}\)
	\(-9\mathrm{i}\)

Cho số phức \(z_1=1+7\mathrm{i}\), \(z_2=3-4\mathrm{i}\). Tính môđun của số phức \(z_1+z_2\).

	\(\left|z_1+z_2\right|=\sqrt{5}\)
	\(\left|z_1+z_2\right|=2\sqrt{5}\)
	\(\left|z_1+z_2\right|=25\sqrt{2}\)
	\(\left|z_1+z_2\right|=5\)

Cho hai số phức \(z_1=1+2\mathrm{i}\) và \(z_2=2-3\mathrm{i}\). Phần ảo của số phức \(w=3z_1-2z_2\) là

	\(11\)
	\(12\)
	\(1\)
	\(12\mathrm{i}\)

Tìm phần thực và phần ảo của số phức $$z=2-\mathrm{i}+\left(\dfrac{1}{3}-2\mathrm{i}\right)$$

	\(\dfrac{7}{3}\) và \(-3\mathrm{i}\)
	\(\dfrac{7}{3}\) và \(-3\)
	\(\dfrac{7}{3}\) và \(2\)
	\(\dfrac{5}{3}\) và \(\dfrac{1}{2}\)

Cho hai số phức \(z_1=2+3\mathrm{i}\) và \(z_2=-4-5\mathrm{i}\). Tìm \(z=z_1+z_2\).

	\(z=-2-2\mathrm{i}\)
	\(z=-2+2\mathrm{i}\)
	\(z=2+2\mathrm{i}\)
	\(z=2-2\mathrm{i}\)

Cho hai số phức \(z_1=4-3\mathrm{i}\) và \(z_2=7+3\mathrm{i}\). Tìm số phức \(z=z_1-z_2\).

	\(z=3+6\mathrm{i}\)
	\(z=11\)
	\(z=-1-10\mathrm{i}\)
	\(z=-3-6\mathrm{i}\)

Cho số phức \(z=2+b\mathrm{i}\). Tính \(z\cdot\overline{z}\).

	\(z\cdot\overline{z}=\sqrt{4+b^2}\)
	\(z\cdot\overline{z}=4-b^2\)
	\(z\cdot\overline{z}=-b\)
	\(z\cdot\overline{z}=4+b^2\)

Thu gọn số phức \(z=\mathrm{i}+(2-4\mathrm{i})-(3-2\mathrm{i})\) ta được

	\(z=-1-\mathrm{i}\)
	\(z=1-\mathrm{i}\)
	\(z=-1-2\mathrm{i}\)
	\(z=1+\mathrm{i}\)

Tìm số phức \(w=z_1-2z_2\), biết rằng \(z_1=1+2\mathrm{i}\) và \(z_2=2-3\mathrm{i}\).

	\(w=3-\mathrm{i}\)
	\(w=5+8\mathrm{i}\)
	\(w=-3+8\mathrm{i}\)
	\(w=-3-4\mathrm{i}\)

Cho số phức \(z\), khi đó \(z+\overline{z}\) là

	Số thực
	Số ảo
	\(0\)
	\(2\)

Cho số phức \(z=-\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}\mathrm{i}\). Tìm số phức \(w=1+z+z^2\).

	\(w=-\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}\mathrm{i}\)
	\(w=0\)
	\(w=1\)
	\(w=2-\sqrt{3}\mathrm{i}\)

Cho \(z_1=1+2\mathrm{i}\), \(z_2=2-3\mathrm{i}\). Khi đó \(w=z_1-2z_2\) bằng

	\(5+8\mathrm{i}\)
	\(-3+8\mathrm{i}\)
	\(3-\mathrm{i}\)
	\(-3-4\mathrm{i}\)

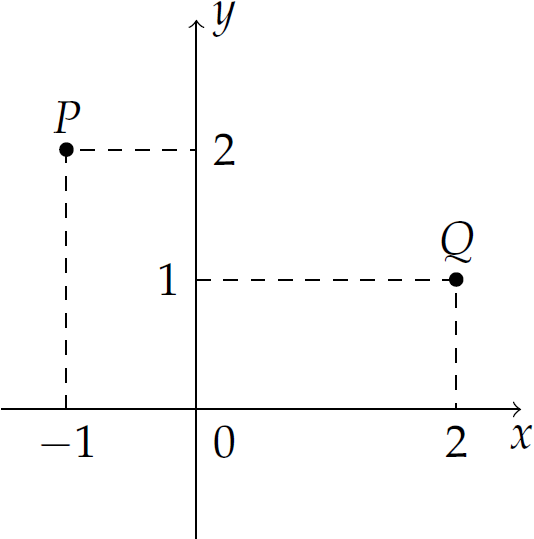
Trong hình vẽ, điểm \(P\) biểu diễn số phức \(z_1\), điểm \(Q\) biểu diễn số phức \(z_2\). Tìm số phức \(z=z_1+z_2\).

	\(z=1+3\mathrm{i}\)
	\(z=-3+\mathrm{i}\)
	\(z=-1+2\mathrm{i}\)
	\(z=2+\mathrm{i}\)

Số phức \(z=(1+2\mathrm{i})(2-3\mathrm{i})\) bằng

	\(8-\mathrm{i}\)
	\(8\)
	\(8+\mathrm{i}\)
	\(-4+\mathrm{i}\)

Cho số phức \(z=a+bi\;(a,\,b\in\mathbb{R})\), trong các mệnh đề sau, đâu là mệnh đề đúng?

	\(z+\overline{z}=2bi\)
	\(z-\overline{z}=2a\)
	\(z\cdot\overline{z}=a^2-b^2\)
	\(\left|z^2\right|=|z|^2\)

Cho \(z\) là một số phức. Xét các mệnh đề sau:

1. Nếu \(z=\overline{z}\) thì \(z\) là số thực.
2. Môđun của \(z\) bằng độ dài đoạn \(OM\), với \(O\) là gốc tọa độ và \(M\) là điểm biểu diễn của số phức \(z\).
3. \(|z|=\sqrt{z\cdot\overline{z}}\)

Có bao nhiêu mệnh đề đúng?

	\(0\)
	\(1\)
	\(2\)
	\(3\)

Cho số phức \(z\) thỏa mãn $$\overline{z}=\dfrac{4(-3+i)}{1-2i}+\dfrac{(3-i)^2}{-i}$$Môđun của số phức \(w=z-i\overline{z}+1\) là

	\(|w|=\sqrt{85}\)
	\(|w|=4\sqrt{5}\)
	\(|w|=6\sqrt{3}\)
	\(|w|=\sqrt{48}\)

Cho các số phức \(z_1=2+3i\), \(z_2=5-i\). Giá trị của biểu thức \(\left|z_1+\dfrac{z_2}{\overline{z_1}}\right|\) là

	\(\sqrt{5}\)
	\(5\)
	\(13\)
	\(\sqrt{11}\)