Tìm tất cả giá trị của tham số \(m\) để đồ thị hàm số \(y=x^4+(6m-4)x^2+1-m\) có \(3\) điểm cực trị.

	\(m\geq\dfrac{2}{3}\)
	\(m\leq\dfrac{2}{3}\)
	\(m>\dfrac{2}{3}\)
	\(m<\dfrac{2}{3}\)

Cho hàm số \(y=f(x)\) có bảng biến thiên như hình vẽ.

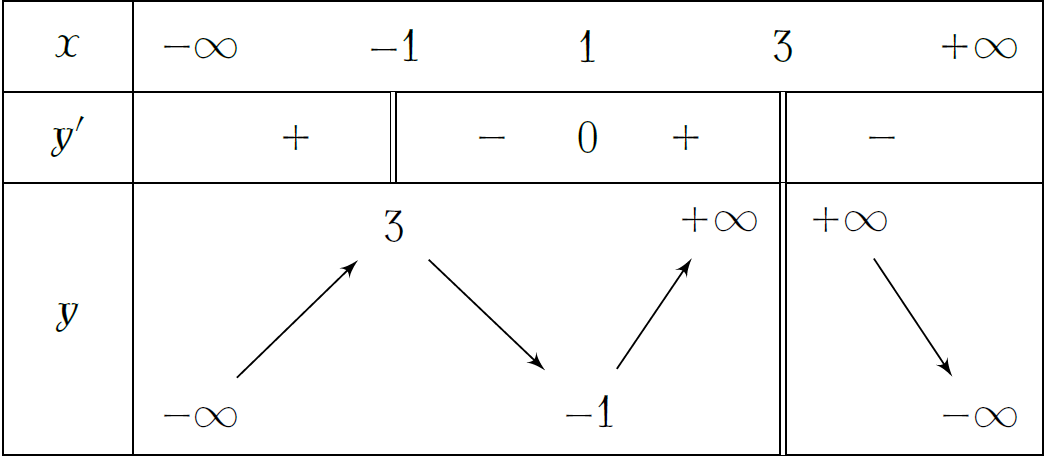
Số điểm cực trị của hàm số \(y=f(x)\) là

	\(0\)
	\(2\)
	\(3\)
	\(1\)

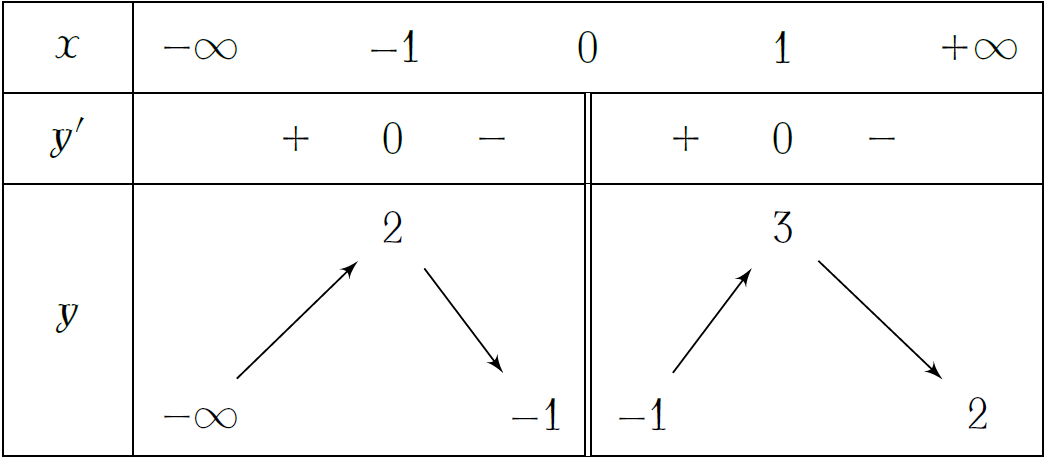
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình vẽ. Hỏi hàm số \(y=f(x)\) có bao nhiêu điểm cực trị?

	\(1\)
	\(3\)
	\(2\)
	\(4\)

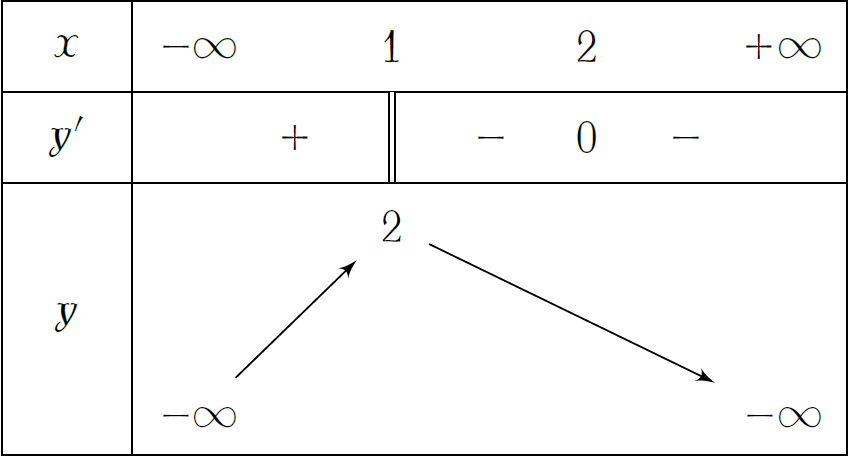
Cho hàm số \(y=f(x)\) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ. Khẳng định nào sau đây là đúng?

	Hàm số có giá trị cực đại bằng \(1\)
	Hàm số có đúng \(2\) cực trị
	Hàm số có giá trị cực đại bằng \(2\)
	Hàm số không xác định tại \(x=1\)

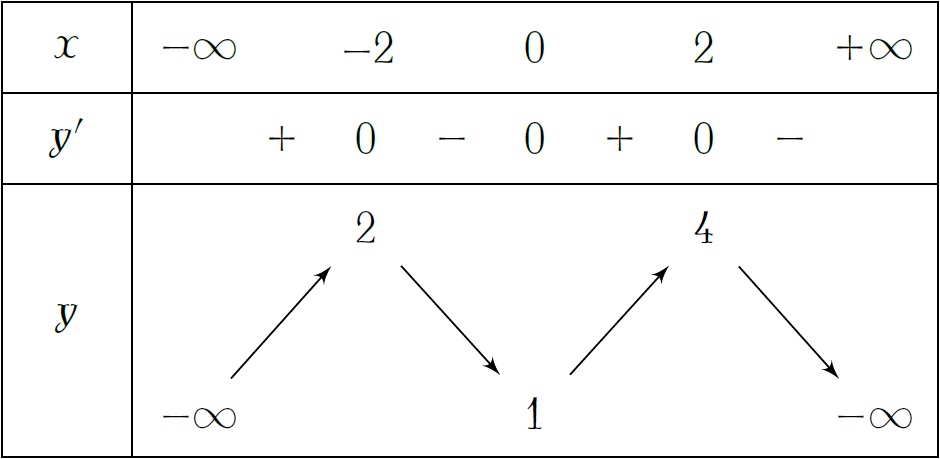
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình. Phát biểu nào sau đây đúng?

	Hàm số đạt cực đại tại \(x=2\)
	Hàm số đạt cực đại tại \(x=4\)
	Hàm số có \(3\) cực tiểu
	Hàm số có giá trị cực tiểu là \(0\)

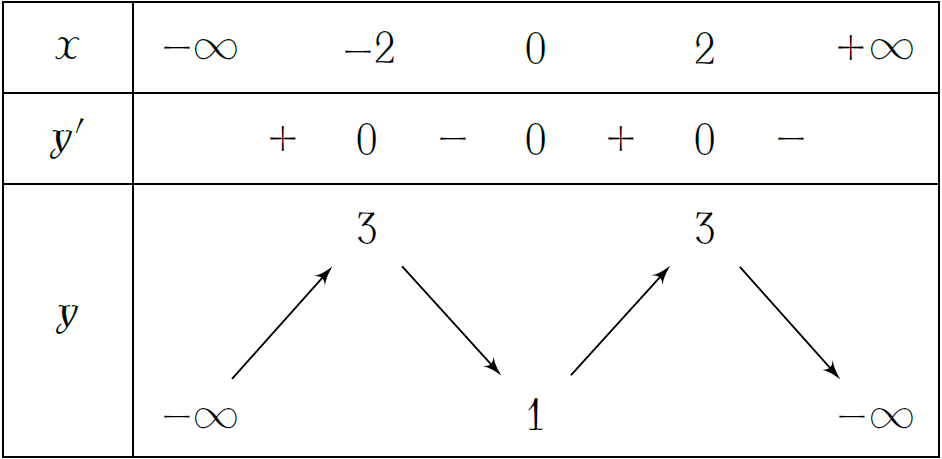
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình. Giá trị cực đại của hàm số bằng

	\(-2\)
	\(-1\)
	\(2\)
	\(3\)

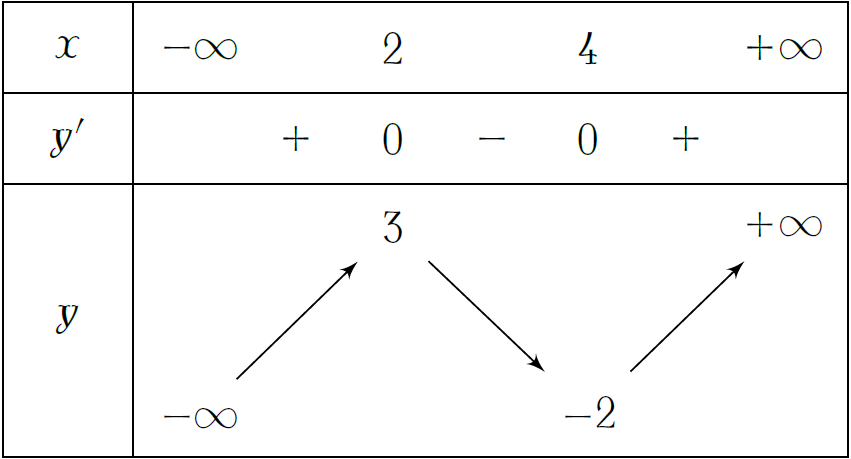
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình. Khẳng định nào sau đây là khẳng định đúng?

	Hàm số đạt cực đại tại \(x=2\)
	Hàm số đạt cực đại tại \(x=-2\)
	Hàm số đạt cực đại tại \(x=4\)
	Hàm số đạt cực đại tại \(x=3\)

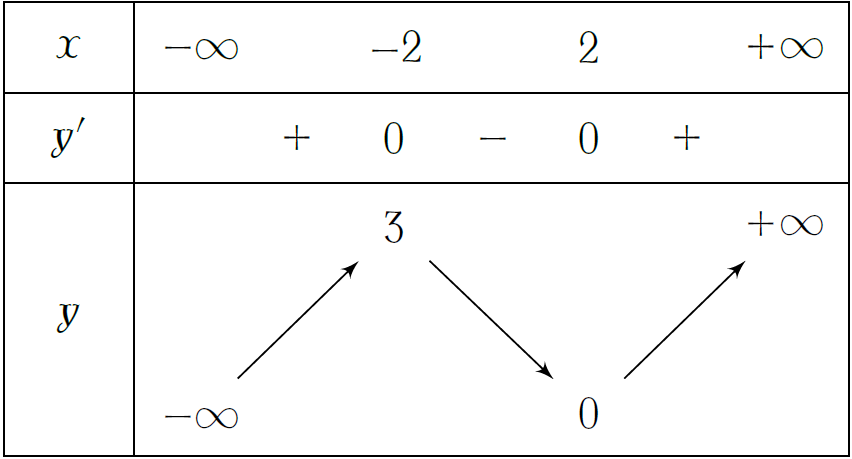
Cho hàm số \(y=f(x)\) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình. Tìm giá trị cực đại \(y_{\text{CĐ}}\) và giá trị cực tiểu \(y_{\text{CT}}\) của hàm số đã cho.

	\(y_{\text{CĐ}}=-2\) và \(y_{\text{CT}}=2\)
	\(y_{\text{CĐ}}=3\) và \(y_{\text{CT}}=0\)
	\(y_{\text{CĐ}}=2\) và \(y_{\text{CT}}=0\)
	\(y_{\text{CĐ}}=3\) và \(y_{\text{CT}}=-2\)

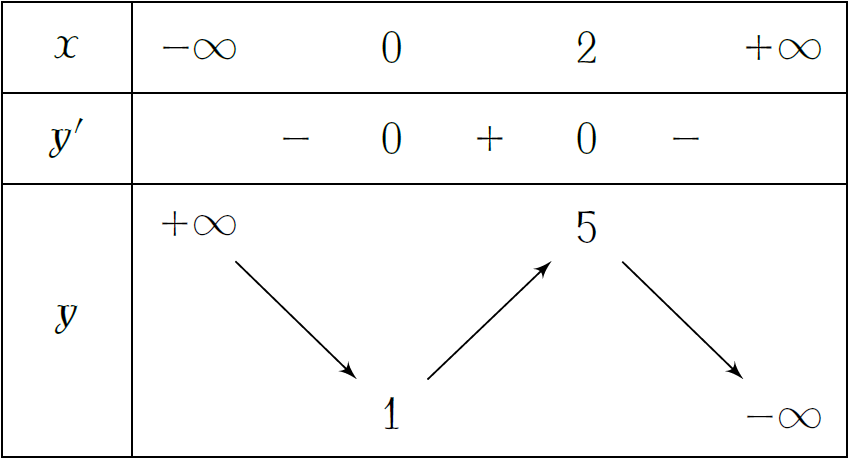
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình. Giá trị cực đại của hàm số bằng

	\(1\)
	\(2\)
	\(0\)
	\(5\)

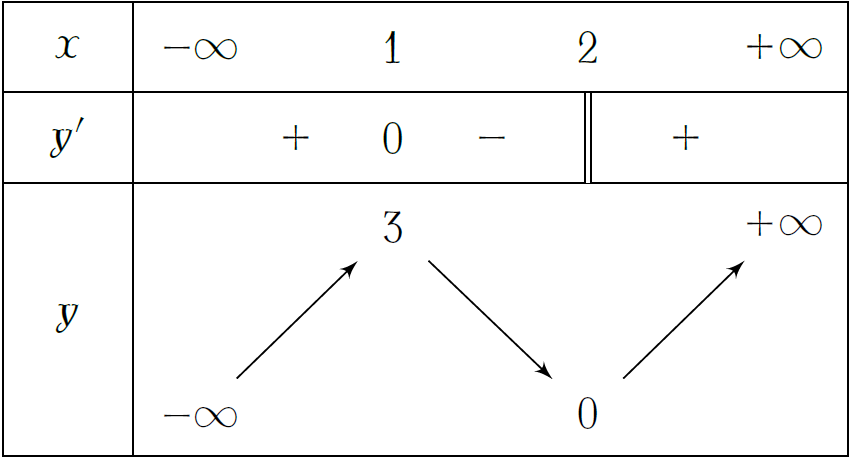
Hàm số \(y=f(x)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây là đúng?

	\(f(x)\) có \(2\) điểm cực trị
	\(f(x)\) có đúng \(1\) điểm cực trị
	\(f(x)\) không có giá trị cực tiểu
	\(f(x)\) không có giá trị cực đại

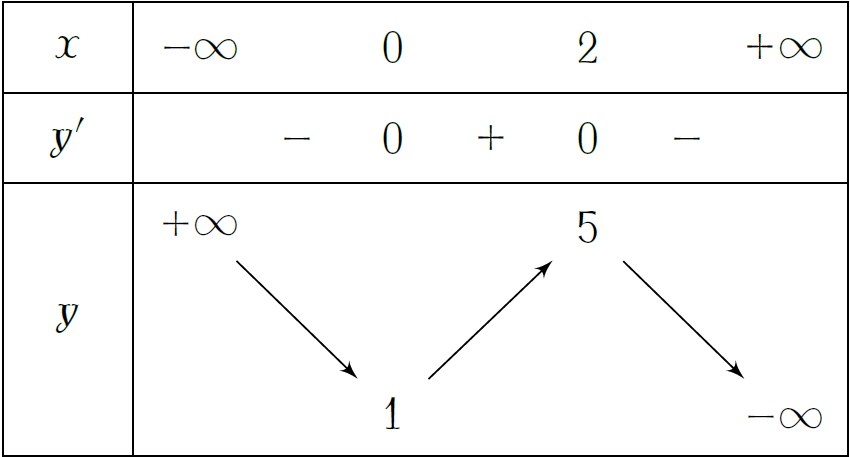
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình trên. Hàm số đạt cực tiểu tại điểm

	\(x=1\)
	\(x=5\)
	\(x=2\)
	\(x=0\)

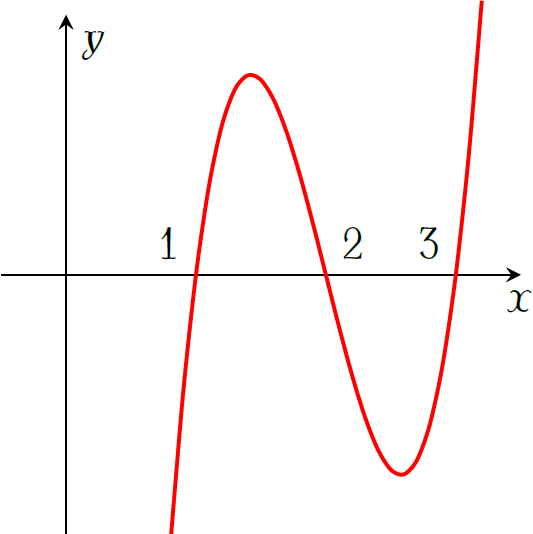
Cho hàm số \(y=f(x)\) liên tục trên \(\mathbb{R}\). Hàm số \(y=f'(x)\) có đồ thị như hình vẽ bên. Khẳng định nào sau đây đúng?

	Đồ thị hàm số \(y=f(x)\) có \(2\) điểm cực trị
	Đồ thị hàm số \(y=f(x)\) có \(3\) điểm cực trị
	Đồ thị hàm số \(y=f(x)\) có \(1\) điểm cực trị
	Đồ thị hàm số \(y=f(x)\) có \(4\) điểm cực trị

Cho hàm số \(y=f(x)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ bên. Đồ thị hàm số đã cho có bao nhiêu điểm cực trị?

	\(4\)
	\(5\)
	\(2\)
	\(3\)

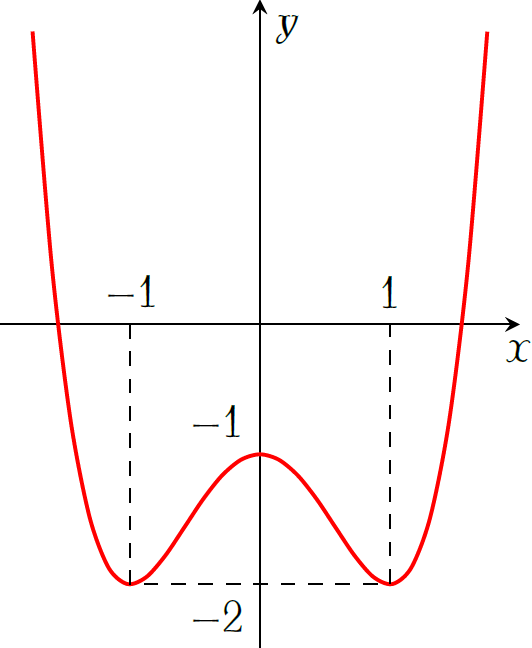
Cho hàm số \(y=f(x)\) có đồ thị như hình vẽ trên. Giá trị cực đại của hàm số là

	\(-2\)
	\(0\)
	\(-1\)
	\(1\)

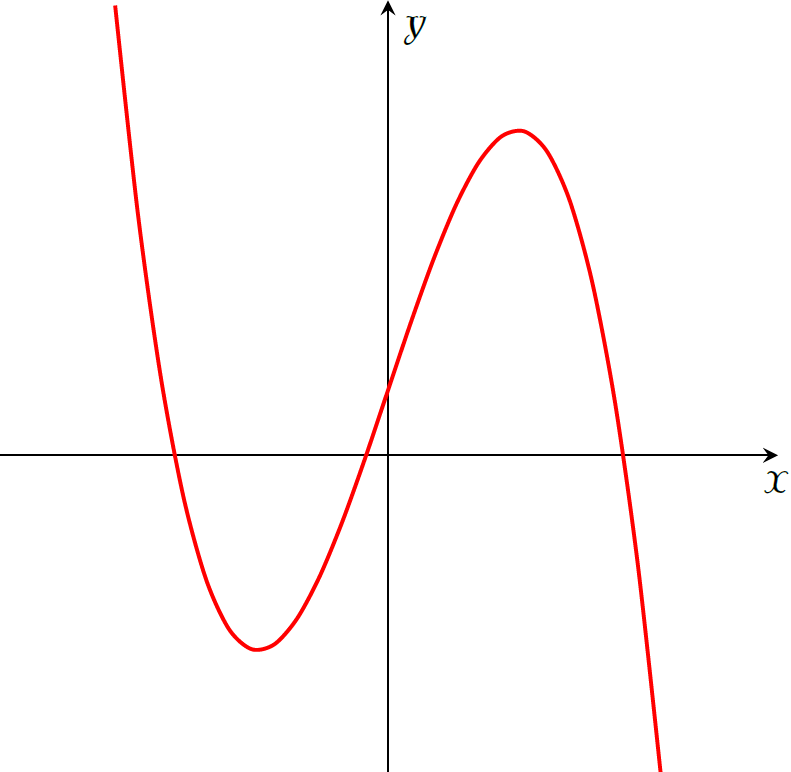
Cho hàm số \(y=f(x)\) có đồ thị như hình vẽ bên. Hàm số đã cho có mấy điểm cực trị?

	\(0\)
	\(4\)
	\(2\)
	\(1\)

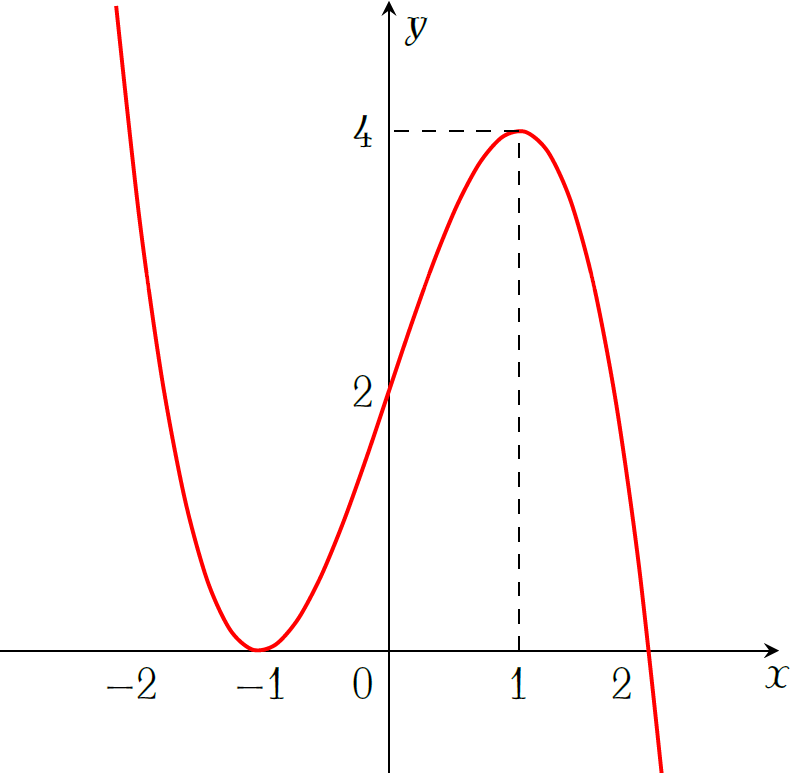
Cho hàm số \(y=f(x)\) xác định, liên tục trên đoạn \([-2;2]\) và có đồ thị là đường cong trong hình vẽ trên. Hàm số đã cho đạt cực tiểu tại điểm

	\(x=1\)
	\(x=-2\)
	\(x=2\)
	\(x=-1\)

Biết rằng đồ thị hàm số \(y=x^3-3x+1\) có hai điểm cực trị \(A,\,B\). Khi đó đường thẳng \(AB\) có phương trình là

	\(y=2x-1\)
	\(y=x-2\)
	\(y=-x+2\)
	\(y=1-2x\)

Cho hàm số \(f(x)\) có đạo hàm \(f'(x)=(x+1)\left(x^2-x\right)(x-1)\), \(\forall x\in\mathbb{R}\). Số điểm cực trị của hàm số đã cho là

	\(1\)
	\(3\)
	\(2\)
	\(0\)

Cho hàm số \(f(x)\) có đạo hàm \(f'(x)=(x+1)^2(x+2)^3(2x-3)\), \(\forall x\in\mathbb{R}\). Số điểm cực trị của hàm số đã cho là

	\(3\)
	\(2\)
	\(0\)
	\(1\)

Cho hàm số \(f(x)\) có đạo hàm \(f'(x)=(x-1)(x-2)^2(x-3)^3(x-4)^4\), \(\forall x\in\mathbb{R}\). Số điểm cực trị của hàm số đã cho là

	\(3\)
	\(5\)
	\(2\)
	\(4\)