Tìm tất cả các giá trị của tham số \(m\) để hàm số $$y=-\dfrac{x^3}{3}-mx^2+(2m-3)x-m+2$$nghịch biến trên \(\mathbb{R}\).
| \(m\in(-\infty;-3)\cup(1;+\infty)\) | |
| \(m\in[-3;1]\) | |
| \(m\in(-\infty;1]\) | |
| \(m\in(-3;1)\) |
Tìm tất cả các giá trị của tham số \(m\) để hàm số $$y=-\dfrac{x^3}{3}+mx^2-(2m+3)x+4$$nghịch biến trên \(\mathbb{R}\).
| \(-1\leq m\leq3\) | |
| \(-3< m<1\) | |
| \(-1< m<3\) | |
| \(-3\leq m\leq1\) |
Cho hàm số \(y=f(x)\). Biết rằng \(f(x)\) có đạo hàm \(f'(x)\) với đồ thị như hình vẽ.
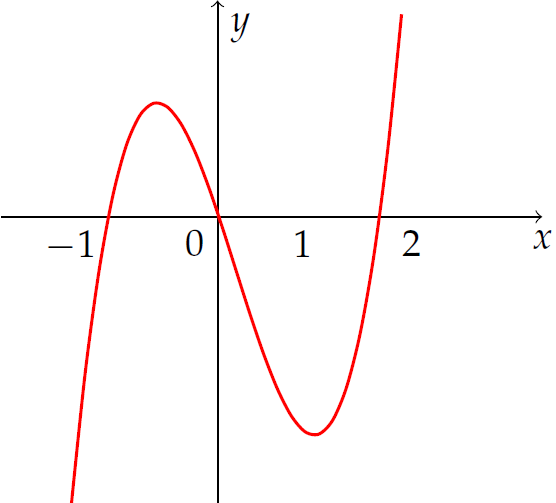
Khẳng định nào sau đây đúng về hàm số \(y=f(x)\)?
| Hàm số đồng biến trên khoảng \((-\infty;-1)\) | |
| Hàm số đồng biến trên khoảng \((-1;0)\) | |
| Hàm số đồng biến trên khoảng \((1;2)\) | |
| Hàm số nghịch biến trên khoảng \((0;+\infty)\) |
Cho hàm số \(y=f(x)\). Biết rằng \(f(x)\) có đạo hàm \(f'(x)\) với đồ thị như hình vẽ.
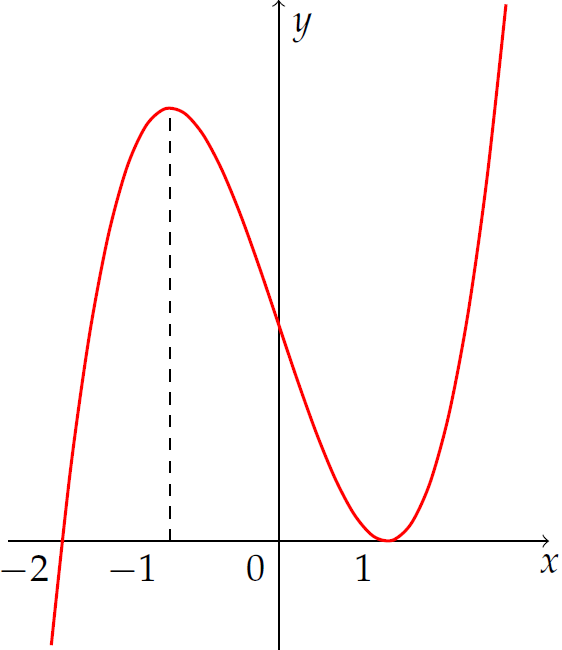
Khẳng định nào sau đây sai?
| Hàm số \(y=f(x)\) nghịch biến trên khoảng \((-\infty;-2)\) | |
| Hàm số \(y=f(x)\) đồng biến trên khoảng \((1;+\infty)\) | |
| Hàm số \(y=f(x)\) luôn tăng trên khoảng \((-1;1)\) | |
| Hàm số \(y=f(x)\) giảm trên đoạn có độ dài bằng \(2\) |
Cho hàm số \(y=x^3+3x^2-4\) có bảng biến thiên như hình vẽ. Tìm \(a\) và \(b\).
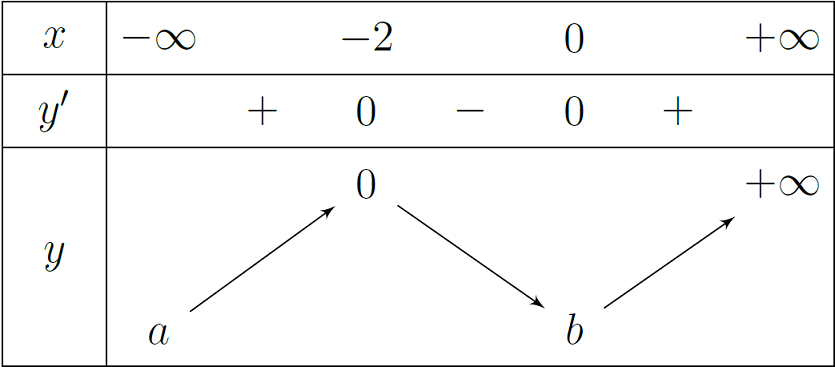
| \(a=+\infty,\;b=2\) | |
| \(a=-\infty,\;b=-4\) | |
| \(a=-\infty,\;b=1\) | |
| \(a=+\infty,\;b=3\) |
Cho hàm số \(y=f(x)\) có bảng xét dấu đạo hàm như sau:

Mệnh đề nào sau đây là đúng?
| Hàm số nghịch biến trên khoảng \((-\infty;-2)\) | |
| Hàm số đồng biến trên khoảng \((-\infty;0)\) | |
| Hàm số nghịch biến trên khoảng \((0;2)\) | |
| Hàm số đồng biến trên khoảng \((-2;0)\) |
Cho hàm số \(y=f(x)\) có bảng biến thiên như sau:
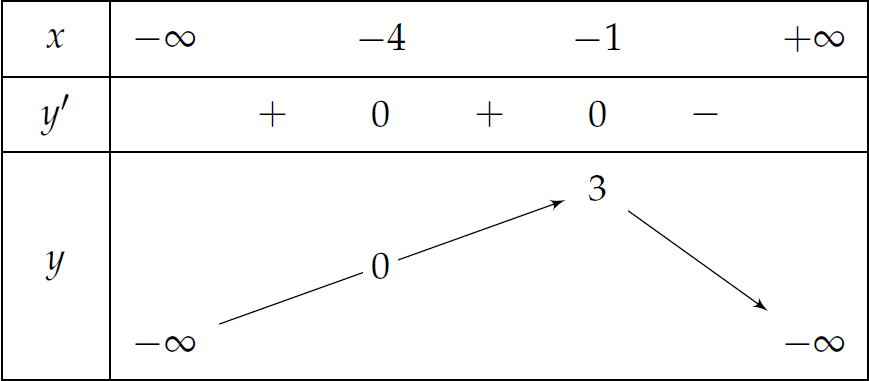
Tìm mệnh đề đúng trong các mệnh đề sau:
| Hàm số đồng biến trên khoảng \((-\infty;3)\) | |
| Hàm số nghịch biến trên khoảng \((-2;+\infty)\) | |
| Hàm số nghịch biến trên khoảng \((-\infty;-2)\) | |
| Hàm số đồng biến trên khoảng \((-4;-1)\) |
Cho hàm số \(y=f(x)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau.
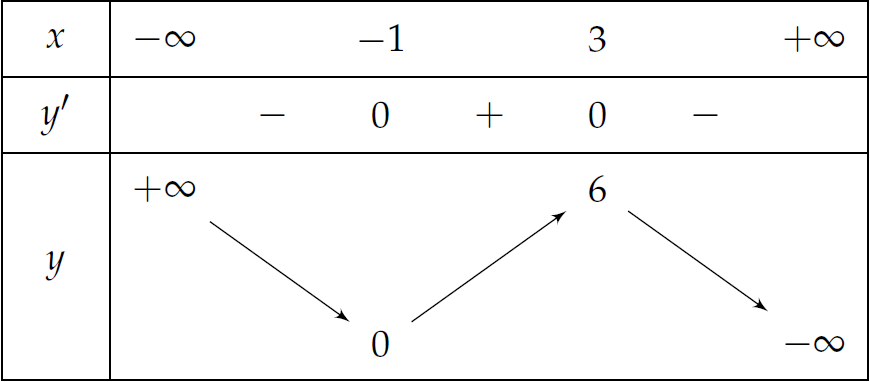
Khẳng định nào sau đây là sai?
| \(f(x)\) nghịch biến trên khoảng \((-\infty;-1)\) | |
| \(f(x)\) đồng biến trên khoảng \((0;6)\) | |
| \(f(x)\) nghịch biến trên khoảng \((3;+\infty)\) | |
| \(f(x)\) đồng biến trên khoảng \((-1;3)\) |
Cho hàm số \(y=f(x)\) có bảng biến thiên như sau.
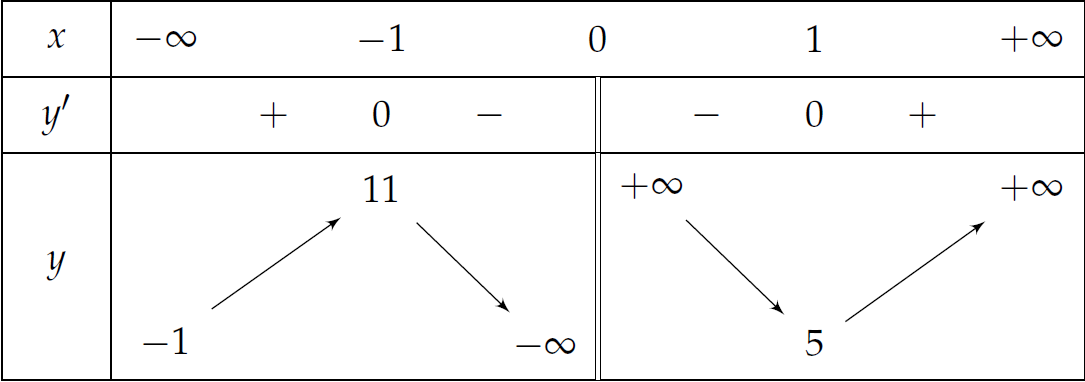
Mệnh đề nào sau đây là đúng?
| Hàm số đồng biến trên khoảng \((-\infty;-1)\cup(1;+\infty)\) và nghịch biến trên khoảng \((-1;0)\cup(0;1)\) | |
| Hàm số đồng biến trên \((-\infty;-1)\) và \((1;+\infty)\), nghịch biến trên \((-1;11)\) | |
| Hàm số đồng biến trên \((-\infty;-1)\) và \((1;+\infty)\), nghịch biến trên \((-1;1)\) | |
| Hàm số đồng biến trên \((-\infty;-1)\) và \((1;+\infty)\), nghịch biến trên \((-1;0)\) và \((0;1)\) |
Cho hàm số \(y=f(x)\) xác định và liên tục trên \(\mathbb{R}\), có bảng biến thiên như sau:

Hàm số đồng biến trên khoảng
| \((-\infty;0)\) | |
| \((0;2)\) | |
| \((0;4)\) | |
| \((2;+\infty)\) |
Cho hàm số \(y=f(x)\) có bảng biến thiên như sau.

Hàm số đồng biến trên khoảng
| \((2;+\infty)\) | |
| \((-2;2)\) | |
| \((-\infty;3)\) | |
| \((0;+\infty)\) |
Cho hàm số \(y=f(x)\) có bảng biến thiên như sau.

Hàm số đồng biến trên khoảng
| \((2;+\infty)\) | |
| \((-\infty;1)\) | |
| \((0;+\infty)\) | |
| \((0;2)\) |
Cho hàm số \(y=f(x)\) có bảng biến thiên như sau:
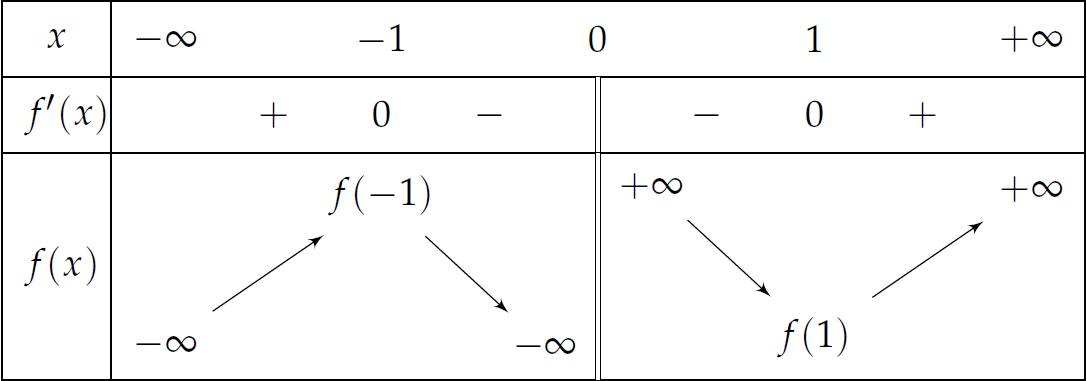
Hàm số nghịch biến trên khoảng nào sau đây?
| \((-1;0)\) | |
| \((-1;1)\) | |
| \((-\infty;-1)\) | |
| \((0;+\infty)\) |
Cho hàm số \(y=f(x)\) có bảng biến thiên như sau:
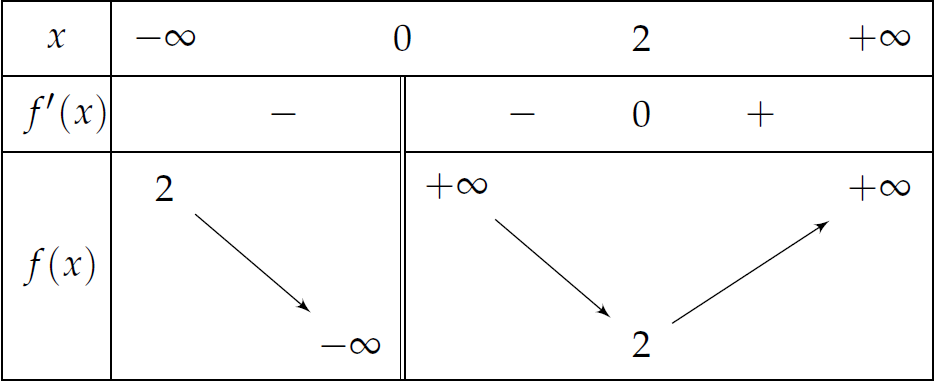
Hàm số nghịch biến trên khoảng nào sau đây?
| \((-\infty;2)\) | |
| \((0;2)\) | |
| \((2;+\infty)\) | |
| \((0;+\infty)\) |
Cho hàm số \(y=f(x)\) có bảng biến thiên như sau:
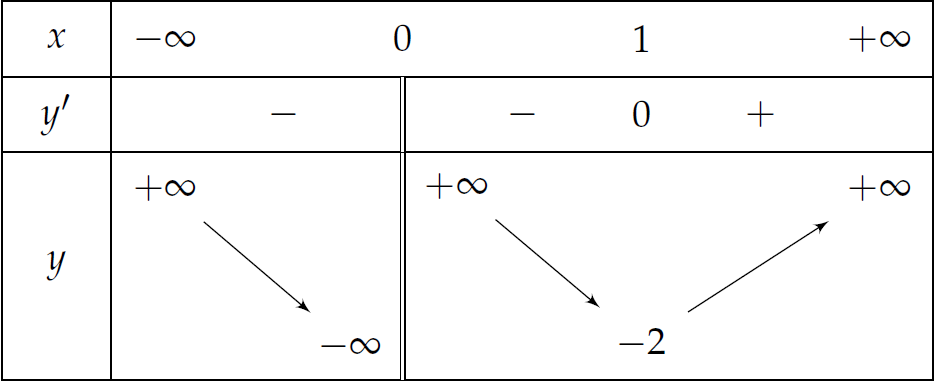
Khẳng định nào sau đây sai?
| Hàm số nghịch biến trên khoảng \((-\infty;-1)\) | |
| Hàm số nghịch biến trên khoảng \((0;1)\) | |
| Hàm số đồng biến trên khoảng \((0;1)\) | |
| Hàm số đồng biến trên khoảng \((2;+\infty)\) |
Cho hàm số \(y=f(x)\) có bảng biến thiên như sau:
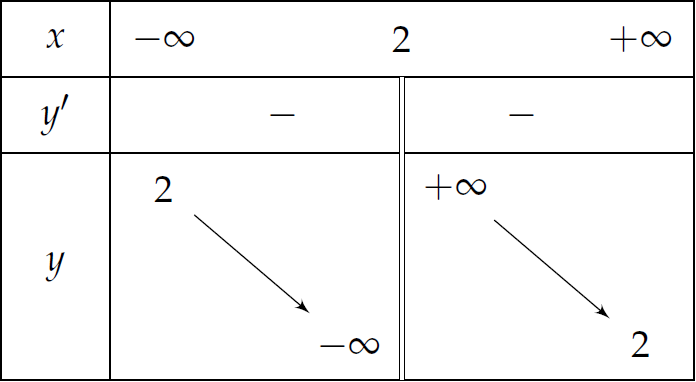
Khẳng định nào sau đây là đúng?
| Hàm số nghịch biến trên \(\mathbb{R}\setminus\{2\}\) | |
| Hàm số đồng biến trên \((-\infty;2)\) và \((2;+\infty)\) | |
| Hàm số nghịch biến trên \((-\infty;2)\) và \((2;+\infty)\) | |
| Hàm số nghịch biến trên \(\mathbb{R}\) |
Cho hàm số \(y=f(x)\) có bảng biến thiên như sau:
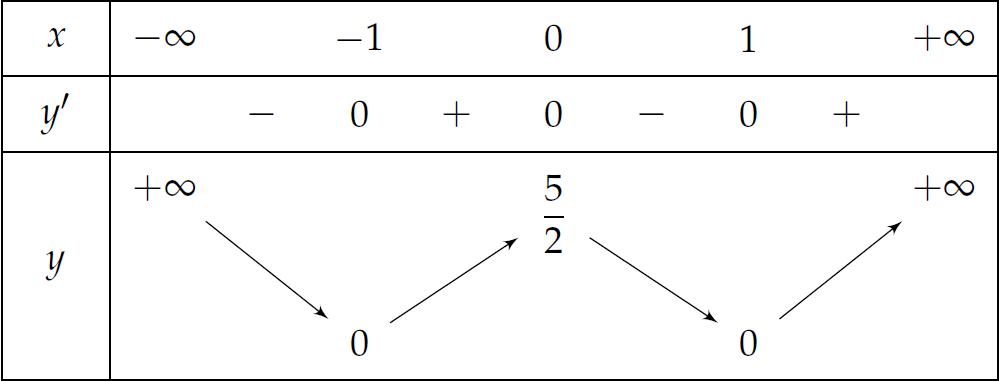
Hàm số nghịch biến trên khoảng nào sau đây?
| \((0;+\infty)\) | |
| \((-\infty;0)\) | |
| \((-1;0)\) | |
| \((-\infty;-2)\) |
Cho hàm số \(y=f(x)\) có bảng biến thiên như sau:

Hàm số đồng biến trên khoảng nào sau đây?
| \((-\infty;0)\) | |
| \((0;2)\) | |
| \((-2;0)\) | |
| \((2;+\infty)\) |
Cho hàm số \(y=f(x)\) có bảng biến thiên như sau:

Hàm số đồng biến trên khoảng nào sau đây?
| \((-\infty;0)\) | |
| \((0;3)\) | |
| \((-1;0)\) | |
| \((0;1)\) |
Cho hàm số \(y=f(x)\) có bảng biến thiên như sau:
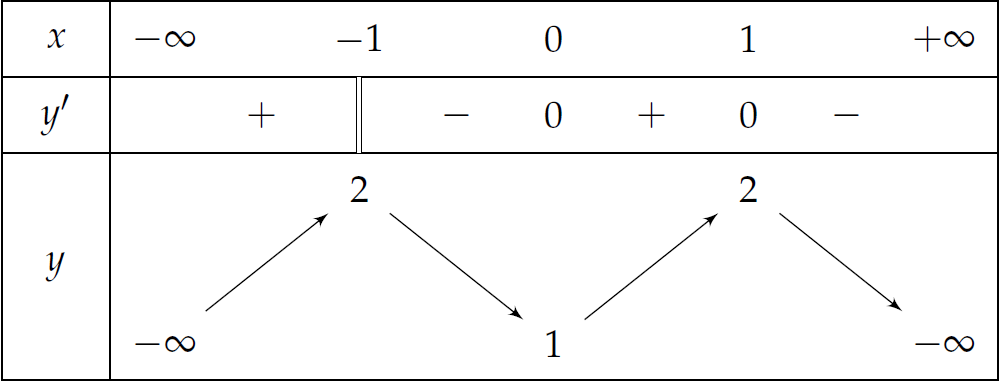
Hàm số nghịch biến trên khoảng nào sau đây?
| \((0;1)\) | |
| \((-1;1)\) | |
| \((-\infty;-1)\) | |
| \((-1;0)\) |
