Cho dãy số hữu hạn \(\left(u_n\right)\) được xác định như sau: \(u_1=-2\), \(u_2=0\), \(u_3=2\), \(u_4=4\), \(u_5=6\). Biết \(u_1\) là số hạng đầu và \(u_5\) là số hạng cuối. Số hạng tổng quát của dãy số trên là

	\(u_n=n-2\)
	\(u_n=-2n\)
	\(u_n=2n-4\)
	\(u_n=-2(n+1)\)

Cho cấp số cộng \(\left(u_n\right)\) biết \(u_n=3-5n\). Tìm công sai \(d\) của \(\left(u_n\right)\).

	\(d=3\)
	\(d=-5\)
	\(d=-3\)
	\(d=5\)

Một cấp số cộng có \(8\) số hạng. Số hạng đầu là \(5\), số hạng thứ tám là \(40\). Khi đó công sai của cấp số cộng đó là

	\(d=4\)
	\(d=5\)
	\(d=7\)
	\(d=6\)

Cho cấp số cộng \(\left(u_n\right)\) có \(u_n=-1\) và \(u_{n+1}=8\). Tính công sai \(d\) của \(\left(u_n\right)\).

	\(d=-9\)
	\(d=7\)
	\(d=-7\)
	\(d=9\)

Dãy số nào sau đây là cấp số cộng?

	\(1,\,3,\,5,\,7,\,9\)
	\(2,\,4,\,5,\,6,\,7\)
	\(1,\,2,\,4,\,8,\,16\)
	\(3,\,-6,\,12,\,-24\)

Trong các dãy số dưới đây, dãy số nào là cấp số cộng?

	\(2,\,8,\,32\)
	\(3,\,7,\,11,\,16\)
	\(\left(u_n\right)\colon u_n=4+3n\)
	\(\left(v_n\right)\colon v_n=n^3\)

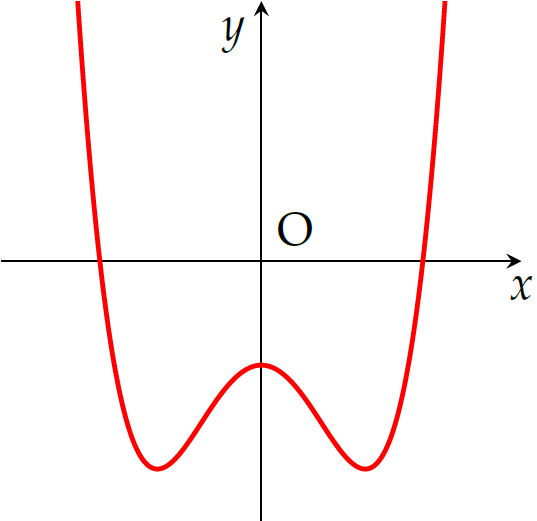
Đường cong ở hình trên là đồ thị của hàm số \(f(x)=ax^4+bx^2+c\); với \(x\) là biến số thực; \(a,\,b,\,c\) là ba hằng số thực, \(a\neq0\). Gọi \(k\) là số nghiệm thực của phương trình \(f(x)=1\). Mệnh đề nào dưới đây đúng?

	\(abc<0\) và \(k=2\)
	\(abc>0\) và \(k=3\)
	\(abc<0\) và \(k=0\)
	\(abc>0\) và \(k=2\)

Tập hợp các tham số thực \(m\) để đồ thị của hàm số \(y=x^3+(m-4)x+2m\) cắt trục hoành tại ba điểm phân biệt là

	\((-\infty;1]\setminus\{-8\}\)
	\((-\infty;1)\setminus\{-8\}\)
	\((-\infty;1]\)
	\((-\infty;1)\)

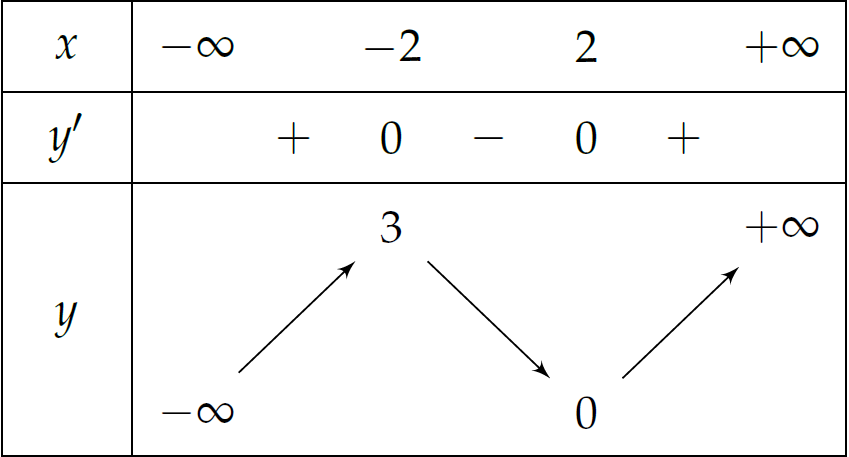
Cho hàm số \(y=f(x)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình trên. Số nghiệm thực của phương trình \(f(x)=1\) bằng

	\(2\)
	\(3\)
	\(1\)
	\(0\)

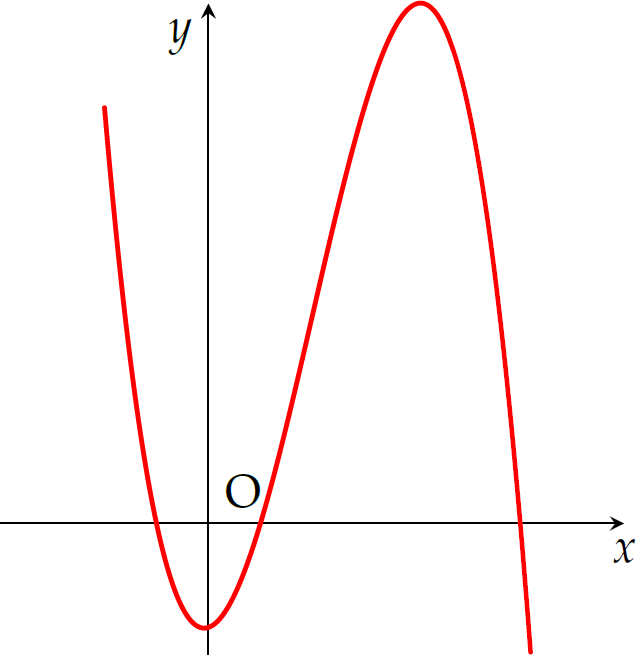
Đường cong ở hình trên là đồ thị của hàm số \(y=ax^3+bx^2+c\); với \(x\) là biến số thực; \(a,\,b,\,c\) là ba hằng số thực, \(a\neq0\). Mệnh đề nào dưới đây đúng?

	\(b<0< a\) và \(c<0\)
	\(a<0< b\) và \(c<0\)
	\(a< b<0\) và \(c<0\)
	\(a<0< b\) và \(c>0\)

Số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\sqrt{x+1}-1}{x^3-4x}\) lần lượt là

	\(3\) và \(1\)
	\(1\) và \(1\)
	\(2\) và \(1\)
	\(1\) và \(0\)

Số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(y=\dfrac{2x^2+2x}{x^2+2x+1}\) lần lượt là

	\(0\) và \(2\)
	\(0\) và \(1\)
	\(1\) và \(2\)
	\(1\) và \(1\)

Tiệm cận ngang của đồ thị hàm số \(y=\sqrt{4x^2-8x+5}+2x\) có phương trình là

	\(y=4\)
	\(y=-2\)
	\(y=2\)
	\(y=-4\)

Cho hàm số \(y=x^4+8x^2+m\) có giá trị nhỏ nhất trên \([1;3]\) bằng \(6\). Tham số thực \(m\) bằng

	\(-42\)
	\(6\)
	\(15\)
	\(-3\)

Cho hàm số \(y=\dfrac{x-m}{x+1}\) thỏa \(\min\limits_{[0;1]}y+\max\limits_{[0;1]}y=5\). Tham số thực \(m\) thuộc tập nào dưới đây?

	\([2;4)\)
	\((-\infty;2)\)
	\([4;6)\)
	\([6;+\infty)\)

Giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\dfrac{1-x}{x+1}\) trên \([-3;-2]\) lần lượt bằng

	\(2\) và \(-3\)
	\(-3\) và \(2\)
	\(3\) và \(-2\)
	\(-2\) và \(-3\)

Số giá trị nguyên của tham số \(m\) để hàm số $$y=x^3-(m+2)x^2+\left(m^2+2m\right)x$$có cực trị là

	\(2\)
	\(1\)
	\(3\)
	\(0\)

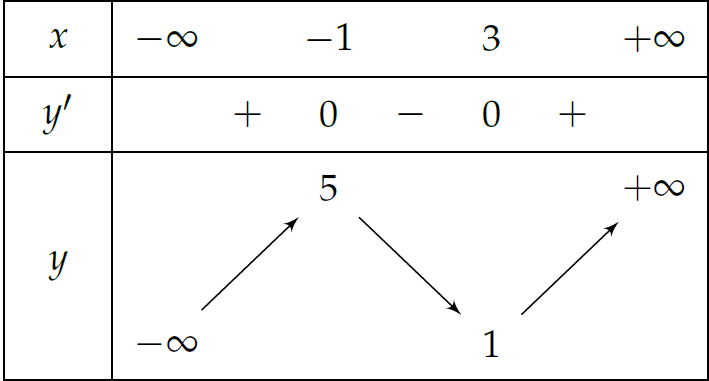
Cho hàm số \(y=f(x)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình trên. Số điểm cực trị của hàm số \(y=\left|f(x-2)-3\right|\) bằng

	\(5\)
	\(4\)
	\(6\)
	\(3\)

Hàm số \(y=x^3+mx^2\) đạt cực đại tại \(x=-2\) khi và chỉ khi giá trị của tham số thực \(m\) bằng

	\(-3\)
	\(3\)
	\(-12\)
	\(12\)

Số điểm cực trị của hàm số \(f(x)\) có đạo hàm \(f'(x)=x(x-1)^2\), \(\forall x\in\mathbb{R}\) là

	\(1\)
	\(2\)
	\(3\)
	\(4\)