Cung có số đo \(x\) (rad) thì có số đo độ là

	\(\dfrac{x\pi}{180}\)
	\(\dfrac{\pi}{180x}\)
	\(\dfrac{180}{x\pi}\)
	\(\dfrac{180x}{\pi}\)

Hình nào dưới đây biểu diễn cung lượng giác \(400^\circ\)?

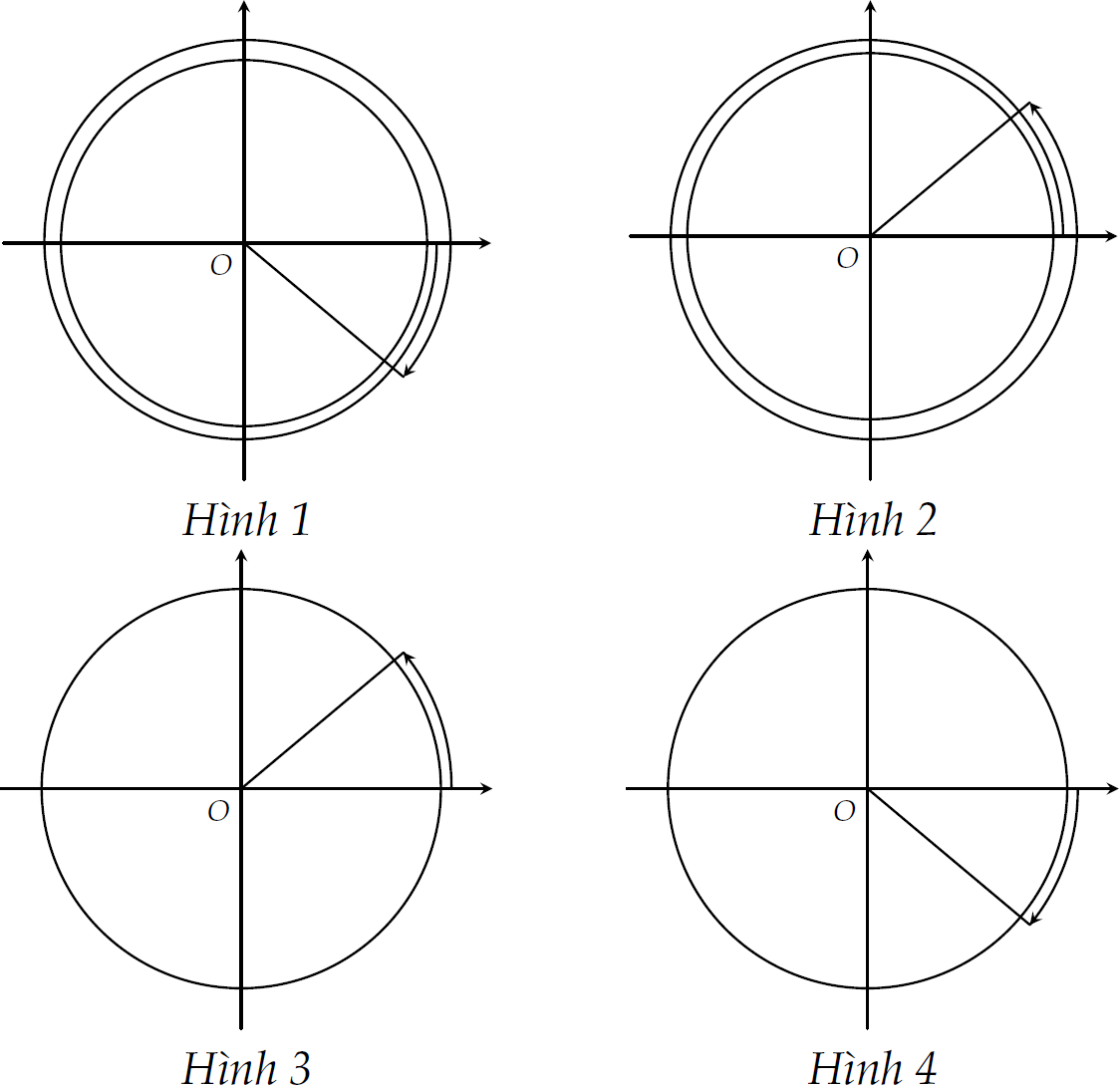
	Hình 1
	Hình 3
	Hình 4
	Hình 2

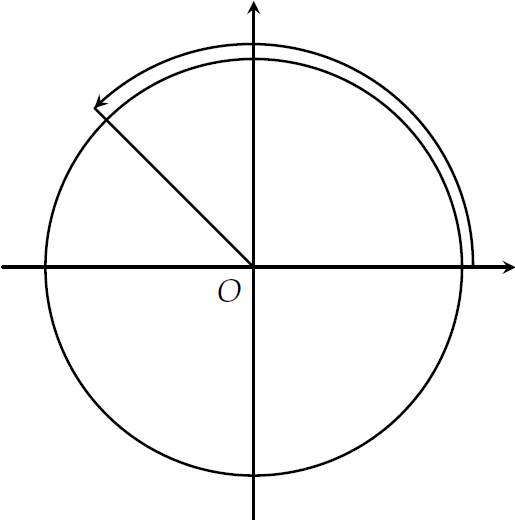
Hình trên mô tả cung tròn có số đo

	\(45^\circ\)
	\(135^\circ\)
	\(120^\circ\)
	\(150^\circ\)

Phát biểu nào sau đây không đúng về đường tròn lượng giác:

	Tâm \(O(0;0)\)
	Là đường tròn định hướng
	Có đường kính bằng \(1\)
	Có bán kính bằng \(1\)

Bảng 1. Lượng nước bạn Bảo Anh đã uống trong 31 ngày (đơn vị: lít)

Mức chênh lệch giữa các ngày trong bảng thống kê trên là

	\(0,87\)
	\(3,69\) lít
	\(0,87\) lít
	\(4,8\) lít

Bảng 1. Lượng nước bạn Bảo Anh đã uống trong 31 ngày (đơn vị: lít)

Phương sai của Bảng 1 là

	\(0,74\)
	\(13,58\)
	\(23\)
	\(0,74\) lít

Bảng 1. Lượng nước bạn Bảo Anh đã uống trong 31 ngày (đơn vị: lít)

Theo Bảng 1, lượng nước trung bình mỗi ngày bạn Bảo Anh uống là

	\(3\) lít
	\(1\) lít
	\(2\) lít
	\(61,7\) lít

Bảng 1. Lượng nước bạn Bảo Anh đã uống trong 31 ngày (đơn vị: lít)

Theo Bảng 1, phép tính nào sau đây chưa đúng:

	\(s^2=\dfrac{1}{31}\left(1(7-2)^2+2(14-2)^2+3(8-2)^2+4(2-2)^2\right)\)
	\(N=7+14+8+2\)
	\(s=\sqrt{s^2}\)
	\(\overline{x}=\dfrac{1}{31}\left(1\cdot7+2\cdot14+3\cdot8+4\cdot2\right)\)

Đại lượng nào sau đây dùng để đánh giá độ phân tán của các số liệu thống kê?

	Độ lệch chuẩn
	Trung bình cộng
	Tổng tần số
	Tần suất

Công thức \(\dfrac{1}{N}\left(n_1x_1+n_2x_2+\cdots+n_kx_k\right)\) dùng để tính

	Trung bình cộng
	Tổng tần số
	Độ lệch chuẩn
	Phương sai

Công thức nào sau đây không đúng?

	\(n_5=\dfrac{f_5}{N}\)
	\(f_5=\dfrac{n_5}{N}\)
	\(s=\sqrt{s^2}\)
	\(N=n_1+n_2+\cdots+n_k\)

Tính giới hạn \(\lim\limits_{x\to-3}\left|\dfrac{-x^2-x+6}{x^2+3x}\right|\).

	\(\dfrac{1}{3}\)
	\(\dfrac{2}{3}\)
	\(\dfrac{5}{3}\)
	\(\dfrac{3}{5}\)

Biết rằng \(\lim\limits_{x\to-\sqrt{3}}\dfrac{2x^3+6\sqrt{3}}{3-x^2}=\dfrac{a\sqrt{3}}{b}\) (\(a,\,b\in\mathbb{Z}\)). Tính \(a^2+b^2\).

	\(10\)
	\(25\)
	\(5\)
	\(13\)

Tính giới hạn \(\lim\limits_{x\to-1}\dfrac{x^5+1}{x^3+1}\).

	\(-\dfrac{3}{5}\)
	\(\dfrac{3}{5}\)
	\(-\dfrac{5}{3}\)
	\(\dfrac{5}{3}\)

Tính giới hạn \(\lim\limits_{x\to2}\dfrac{x^3-8}{x^2-4}\).

	\(0\)
	\(+\infty\)
	\(3\)
	Không xác định

Tính giới hạn \(\lim\limits_{x\to+\infty}\left(\sqrt{1+2x^2}-x\right)\).

	\(0\)
	\(+\infty\)
	\(\sqrt{2}-1\)
	\(-\infty\)

Tính giới hạn \(\lim\limits_{x\to-\infty}\left(2x^3-x^2\right)\).

	\(1\)
	\(+\infty\)
	\(-1\)
	\(-\infty\)

Tính giới hạn \(\lim\limits_{x\to-\infty}\dfrac{\sqrt[3]{x^3+2x^2+1}}{\sqrt{2x^2+1}}\).

	\(\dfrac{\sqrt{2}}{2}\)
	\(0\)
	\(-\dfrac{\sqrt{2}}{2}\)
	\(1\)

Tính giới hạn \(\lim\limits_{x\to-\infty}\dfrac{\sqrt{4x^2-x+1}}{x+1}\).

	\(2\)
	\(-1\)
	\(-2\)
	\(+\infty\)

Tính giới hạn \(\lim\limits_{x\to-\infty}\dfrac{2x-3}{\sqrt{x^2+1}-x}\).

	\(-2\)
	\(+\infty\)
	\(3\)
	\(-1\)