Trong mặt phẳng \(Oxy\) cho đường thẳng \(\Delta\) có phương trình \(4x-y+3=0\). Ảnh của đường thẳng \(\Delta\) qua phép tịnh tiến theo vectơ \(\overrightarrow{u}=(2;-1)\) có phương trình

	\(4x-y+5=0\)
	\(4x-y+10=0\)
	\(4x-y-6=0\)
	\(x-4y-6=0\)

Trong mặt phẳng \(Oxy\) nếu một phép tịnh tiến biến điểm \(M(4;2)\) thành điểm \(M'(4;5)\) thì phép tịnh tiến đó biến điểm \(A(2;5)\) thành điểm nào sau đây?

	\(E(5;2)\)
	\(F(1;6)\)
	\(G(2;8)\)
	\(H(2;5)\)

Trong mặt phẳng \(Oxy\) cho hai điểm \(M(-10;1)\) và \(M'(3;8)\). Phép tịnh tiến theo vectơ \(\overrightarrow{v}\) biến điểm \(M\) thành \(M'\). Mệnh đề nào sau đây là đúng?

	\(\overrightarrow{v}=(-13;7)\)
	\(\overrightarrow{v}=(13;-7)\)
	\(\overrightarrow{v}=(13;7)\)
	\(\overrightarrow{v}=(-13;-7)\)

Trong mặt phẳng \(Oxy\) cho điểm \(A(2;5)\). Hỏi \(A\) là ảnh của điểm nào trong các điểm sau qua phép tịnh tiến theo vectơ \(\overrightarrow{v}=(1;2)\)?

	\(M(1;3)\)
	\(N(1;6)\)
	\(P(3;7)\)
	\(Q(2;4)\)

Trong mặt phẳng \(Oxy\) cho vectơ \(\overrightarrow{v}=(-3;2)\) và điểm \(A(1;3)\). Ảnh của điểm \(A\) qua phép tịnh tiến theo vectơ \(\overrightarrow{v}\) là điểm nào sau đây?

	\(M(-3;2)\)
	\(N(1;3)\)
	\(P(-2;5)\)
	\(Q(2;-5)\)

Trong mặt phẳng \(Oxy\) cho điểm \(A(2;5)\). Phép tịnh tiến theo vectơ \(\overrightarrow{v}=(1;2)\) biến \(A\) thành điểm \(A'\) có tọa độ là

	\((3;1)\)
	\((1;6)\)
	\((3;7)\)
	\((4;7)\)

Trong mặt phẳng \(Oxy\) cho phép biến hình $f$ xác định như sau: Với mỗi điểm \(M(x;y)\) có \(M'=f(M)\) sao cho \(M'\left(x';y'\right)\) thỏa mãn \(x'=x+2\) và \(y'=y-3\). Mệnh đề nào sau đây là đúng?

	\(f\) là phép tịnh tiến theo vectơ \(\overrightarrow{v}=(2;3)\)
	\(f\) là phép tịnh tiến theo vectơ \(\overrightarrow{v}=(-2;3)\)
	\(f\) là phép tịnh tiến theo vectơ \(\overrightarrow{v}=(-2;-3)\)
	\(f\) là phép tịnh tiến theo vectơ \(\overrightarrow{v}=(2;-3)\)

Trong mặt phẳng \(Oxy\), cho vectơ \(\overrightarrow{v}=(a;b)\). Giả sử phép tịnh tiến \(\mathrm{T}_{\overrightarrow{v}}\) biến điểm \(M(x;y)\) thành điểm \(M'\left(x';y'\right)\). Khi đó

	\(\begin{cases}x'=x+a\\ y'=y+b\end{cases}\)
	\(\begin{cases}x=x'+a\\ y=y'+b\end{cases}\)
	\(\begin{cases}x'=x-a\\ y'=y-b\end{cases}\)
	\(\begin{cases}x'=ax\\ y'=by\end{cases}\)

Cho phép tịnh tiến theo vectơ \(\overrightarrow{v}\) biến điểm \(A\) thành \(A'\), biến điểm \(M\) thành \(M'\). Mệnh đề nào sau đây là đúng?

	\(\overrightarrow{AM}=\overrightarrow{A'M'}\)
	\(\overrightarrow{AM}=2\overrightarrow{A'M'}\)
	\(\overrightarrow{AM}=-\overrightarrow{A'M'}\)
	\(3\overrightarrow{AM}=2\overrightarrow{A'M'}\)

Cho hình bình hành \(ABCD\). Có bao nhiêu phép tịnh tiến biến đường thẳng \(AB\) thành đường thẳng \(CD\) và biến đường thẳng \(AD\) thành đường thẳng \(BC\)?

	\(0\)
	\(1\)
	\(2\)
	Vô số

Cho hai đường thẳng \(d\) và \(d'\) song song với nhau. Có bao nhiêu phép tịnh tiến biến \(d\) thành \(d'\)?

	\(0\)
	\(1\)
	\(2\)
	Vô số

Có bao nhiêu phép tịnh tiến biến một đường thẳng cho trước thành chính nó?

	\(0\)
	\(1\)
	\(2\)
	Vô số

Có bao nhiêu phép tịnh tiến biến một hình vuông thành chính nó?

	\(0\)
	\(1\)
	\(2\)
	Vô số

Có bao nhiêu phép tịnh tiến biến một đường tròn cho trước thành chính nó?

	\(0\)
	\(1\)
	\(2\)
	Vô số

Mệnh đề nào sau đây là sai?

	Phép tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kì
	Phép tịnh tiến biến ba điểm thẳng hàng thành ba điểm thẳng hàng
	Phép tịnh tiến biến tam giác thành tam giác bằng tam giác đã cho
	Phép tịnh tiến biến đường thẳng thành đường thẳng song song với đường thẳng đã cho

Có bao nhiêu số nguyên \(x\) sao cho tồn tại số thực \(y\) thỏa mãn $$\log_3\left(x+y\right)=\log_4\left(x^2+y^2\right)?$$

	\(3\)
	\(2\)
	\(1\)
	Vô số

Cho hình hộp \(ABCD.A'B'C'D'\) có chiều cao bằng \(8\) và diện tích đáy bằng \(9\). Gọi \(M,\,N,\,P\) và \(Q\) lần lượt là tâm của các mặt bên \(ABB'A'\), \(BCC'B'\), \(CDD'C'\) và \(DAA'D'\). Thể tích của khối đa diện lồi có các đỉnh là các điểm \(A,\,B,\,C,\,D\), \(M,\,N,\,P\) và \(Q\) bằng

	\(27\)
	\(30\)
	\(18\)
	\(36\)

Cho hàm số \(f\left(x\right)=\dfrac{x+m}{x+1}\) (\(m\) là tham số thực). Gọi \(S\) là tập hợp tất cả các giá trị của m sao cho $$\max\limits_{[0;1]}\left|f\left(x\right)\right|+\min\limits_{[0;1]}\left|f\left(x\right)\right|=2.$$Số phần tử của \(S\) là

	\(6\)
	\(2\)
	\(1\)
	\(4\)

Xét các số thực dương \(a,\,b,\,x,\,y\) thỏa mãn \(a>1,\,b>1\) và \(a^x=b^y=\sqrt{ab}\). Giá trị nhỏ nhất của biểu thức \(P=x+2y\) thuộc tập hợp nào dưới đây?

	\(\left(1;2\right)\)
	\(\left[2;\dfrac{5}{2}\right)\)
	\(\left[3;4\right)\)
	\(\left[\dfrac{5}{2};3\right)\)

Cho hàm số \(f\left(x\right)\) có bảng biến thiên như sau:

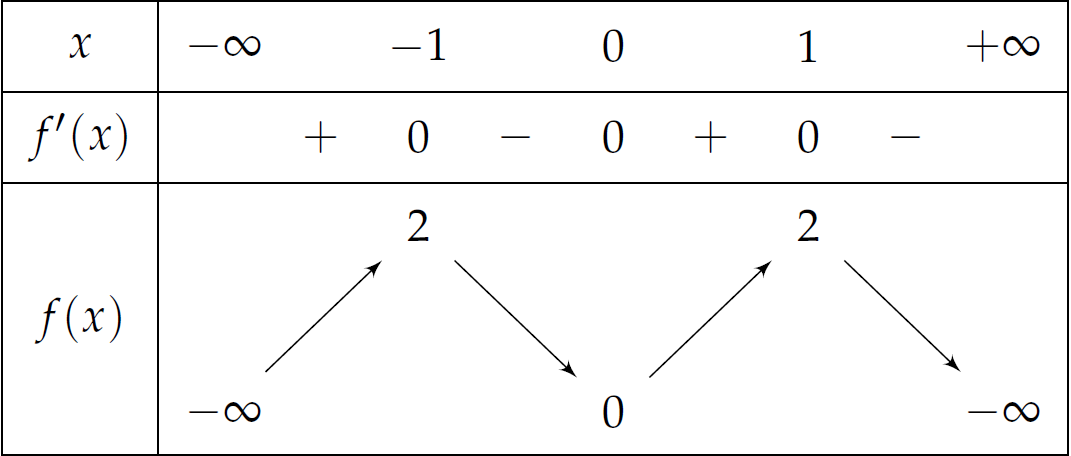
Số nghiệm thuộc đoạn \(\left[0;\dfrac{5\pi}{2}\right]\) của phương trình \(f\left(\sin x\right)=1\) là

	\(7\)
	\(4\)
	\(5\)
	\(6\)