Nếu $\displaystyle\displaystyle\int\limits_0^1f(x)\mathrm{~d}x=2$ và $\displaystyle\displaystyle\int\limits_1^3f(x)\mathrm{~d}x=5$ thì $\displaystyle\displaystyle\int\limits_0^3f(x)\mathrm{~d}x$ bằng
| $10$ | |
| $3$ | |
| $7$ | |
| $-3$ |
Cho số phức $z=1-2i$. Phần ảo của số phức $\overline{z}$ bằng
| $-1$ | |
| $2$ | |
| $1$ | |
| $-2$ |
Trong không gian $Oxyz$, cho hai vectơ $\overrightarrow{u}=(1;2;-2)$ và $\overrightarrow{v}=(2;-2;3)$. Tọa độ của vectơ $\overrightarrow{u}+\overrightarrow{v}$ là
| $(-1;4;-5)$ | |
| $(1;-4;5)$ | |
| $(3;0;1)$ | |
| $(3;0;-1)$ |
Trong không gian $Oxyz$, cho mặt cầu $(S)$ có tâm $I(1;2;-1)$ và bán kính $R=2$. Phương trình của $(S)$ là
| $(x-1)^2+(y-2)^2+(z+1)^2=4$ | |
| $(x-1)^2+(y-2)^2+(z+1)^2=2$ | |
| $(x+1)^2+(y+2)^2+(z-1)^2=2$ | |
| $(x+1)^2+(y+2)^2+(z-1)^2=4$ |
Cho dãy số $\big(u_n\big)$ với $u_n=\dfrac{1}{n+1}$, $\forall n\in\mathbb{N}^*$. Giá trị của $u_3$ bằng
| $4$ | |
| $\dfrac{1}{4}$ | |
| $\dfrac{1}{3}$ | |
| $\dfrac{1}{2}$ |
Cho hàm số $y=\big(2x^2-1\big)^{\tfrac{1}{2}}$. Giá trị của hàm số đã cho tại điểm $x=2$ bằng
| $3$ | |
| $\sqrt{7}$ | |
| $\sqrt{3}$ | |
| $7$ |
Cho khối chóp $S.ABCD$ có chiều cao bằng $4$ và đáy $ABCD$ có diện tích bằng $3$. Thể tích khối chóp đã cho bằng
| $7$ | |
| $5$ | |
| $4$ | |
| $12$ |
Cho hai số phức $z_1=2-i$ và $z_2=1+3i$. Phần thực của số phức $z_1-z_2$ bằng
| $3$ | |
| $-4$ | |
| $1$ | |
| $-1$ |
Cho khối nón có thể tích bằng $12$ và diện tích đáy bằng $9$. Chiều cao của khối nón đã cho bằng
| $\dfrac{4\pi}{3}$ | |
| $\dfrac{4}{3}$ | |
| $4\pi$ | |
| $4$ |
Cho hình trụ có chiều cao $h=3$ và bán kính đáy $r=4$. Diện tích xung quanh của hình trụ đã cho bằng
| $48\pi$ | |
| $16\pi$ | |
| $24\pi$ | |
| $56\pi$ |
Cho hàm số $y=f(x)$ có bảng xét dấu đạo hàm như sau:

Hàm số đã cho đồng biến trên khoảng nào dưới đây?
| $(-\infty;0)$ | |
| $(2;+\infty)$ | |
| $(0;+\infty)$ | |
| $(-1;2)$ |
Điểm $M$ trong hình bên là điểm biểu diễn của số phức nào dưới đây?
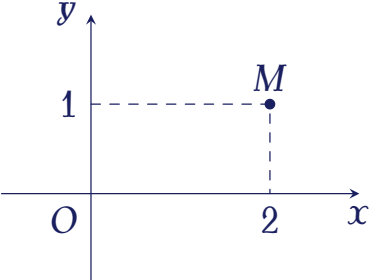
| $2-i$ | |
| $1+2i$ | |
| $1-2i$ | |
| $2+i$ |
Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$. Biết hàm số $F(x)$ là một nguyên hàm của $f(x)$ trên $\mathbb{R}$ và $F(2)=6$, $F(4)=12$. Tích phân $\displaystyle\displaystyle\int\limits_2^4f(x)\mathrm{~d}x$ bằng
| $2$ | |
| $6$ | |
| $18$ | |
| $-6$ |
Nếu khối lăng trụ $ABC.A'B'C'$ có thể tích $V$ thì khối chóp $A'.ABC$ có thể tích bằng
| $\dfrac{V}{3}$ | |
| $V$ | |
| $\dfrac{2V}{3}$ | |
| $3V$ |
Tiệm cận đứng của đồ thị hàm số $y=\dfrac{3x-1}{x-2}$ có phương trình là
| $x=2$ | |
| $x=-2$ | |
| $x=3$ | |
| $x=\dfrac{1}{2}$ |
Cho hàm số bậc ba $y=f(x)$ có đồ thị là đường cong trong hình bên.
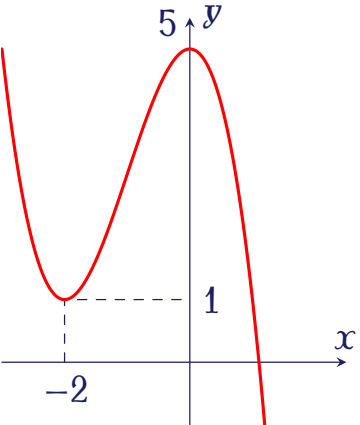
Số nghiệm thực của phương trình $f(x)=2$ là
| $1$ | |
| $0$ | |
| $2$ | |
| $3$ |
Với $b,\,c$ là hai số thực dương tùy ý thỏa mãn $\log_5b\ge\log_5c$, khẳng định nào dưới đây là đúng?
| $b\ge c$ | |
| $b\le c$ | |
| $b>c$ | |
| $b< c$ |
Đạo hàm của hàm số $y=\log_2(x-1)$ là
| $y'=\dfrac{x-1}{\ln2}$ | |
| $y'=\dfrac{1}{\ln2}$ | |
| $y'=\dfrac{1}{(x-1)\ln2}$ | |
| $y'=\dfrac{1}{x-1}$ |
Cho hàm số $f(x)=\cos x-x$. Khẳng định nào dưới đây đúng?
| $\displaystyle\displaystyle\int f(x)\mathrm{~d}x=-\sin x+x^2+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{~d}x=-\sin x-\dfrac{x^2}{2}+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{~d}x=\sin x-x^2+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{~d}x=\sin x-\dfrac{x^2}{2}+C$ |
Có bao nhiêu tam giác mà ba đỉnh của nó được lấy từ các đỉnh của một lục giác đều?
| $729$ | |
| $20$ | |
| $120$ | |
| $216$ |
