Tìm giá trị nhỏ nhất của hàm số \(y=x+1+\dfrac{4}{x}\) trên đoạn \([1;3]\).
| \(4\) | |
| \(\dfrac{16}{3}\) | |
| \(5\) | |
| \(6\) |
Cho hàm số \(y=\tan x\) có đồ thị như hình vẽ:
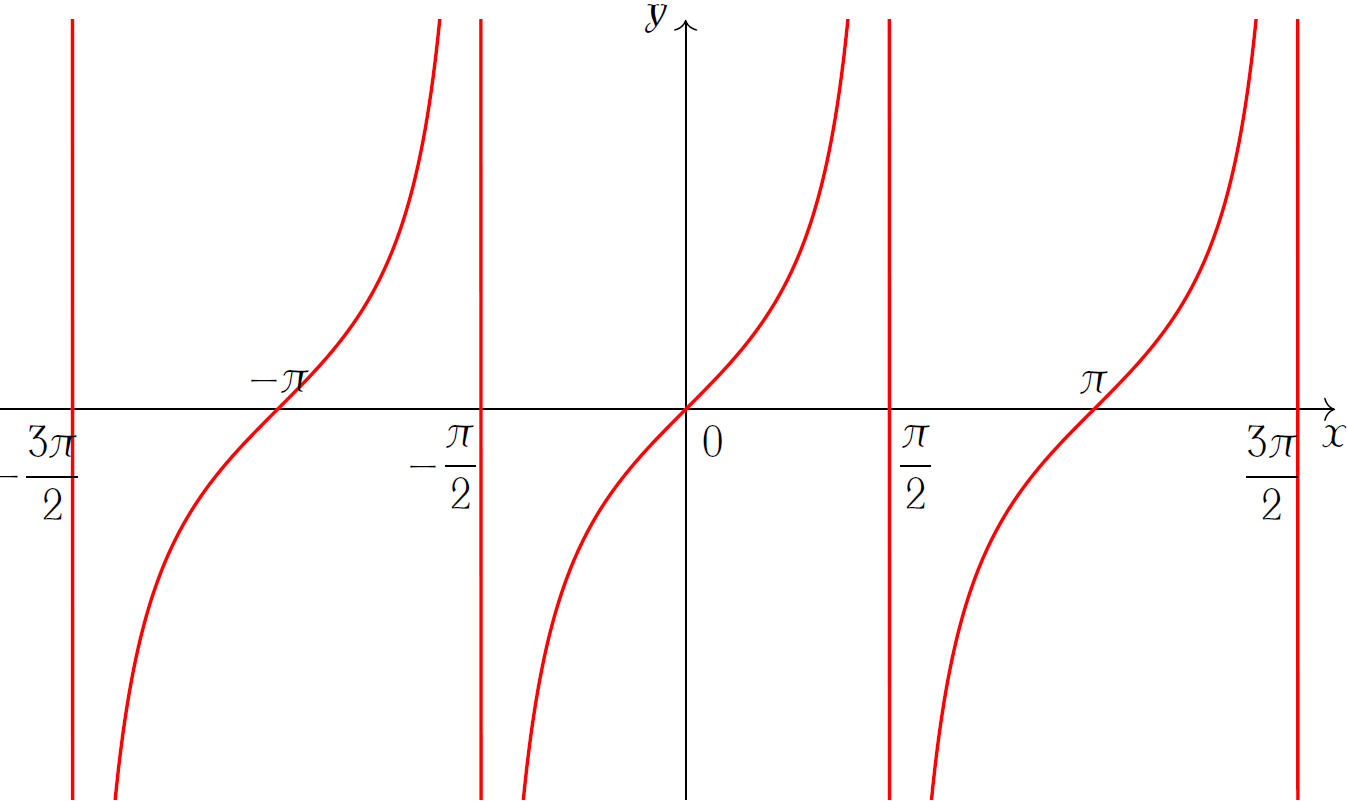
Khẳng định nào sau đây sai?
| Hàm số đồng biến trên \(\left(-\dfrac{\pi}{2};0\right)\) | |
| \(\tan x>0,\forall x\in\left(0;\dfrac{\pi}{2}\right)\) | |
| Đồ thị hàm số luôn cắt trục hoành tại một điểm | |
| Đồ thị hàm số nhận gốc tọa độ \(O\) làm tâm đối xứng nên hàm số \(y=\tan x\) là hàm số lẻ |
Chu kì của hàm số \(f\left(x\right)=\tan\dfrac{x}{2}\) là
| \(T=4\pi\) | |
| \(T=\dfrac{\pi}{2}\) | |
| \(T=\pi\) | |
| \(T=2\pi\) |
Hàm số nào sau đây là hàm số chẵn?
| \(y=\cos x\) | |
| \(y=\sin x\) | |
| \(y=\tan x\) | |
| \(y=\cot x\) |
Hàm số \(y=\sin\left(x+\dfrac{\pi}{3}\right)\) đạt giá trị nhỏ nhất khi
| \(x=-\dfrac{\pi}{3}\) | |
| \(x=0\) | |
| \(x=-\dfrac{5\pi}{6}\) | |
| \(x=-1\) |
Cho đồ thị hàm số \(y=\cos2x\) có đồ thị như hình.
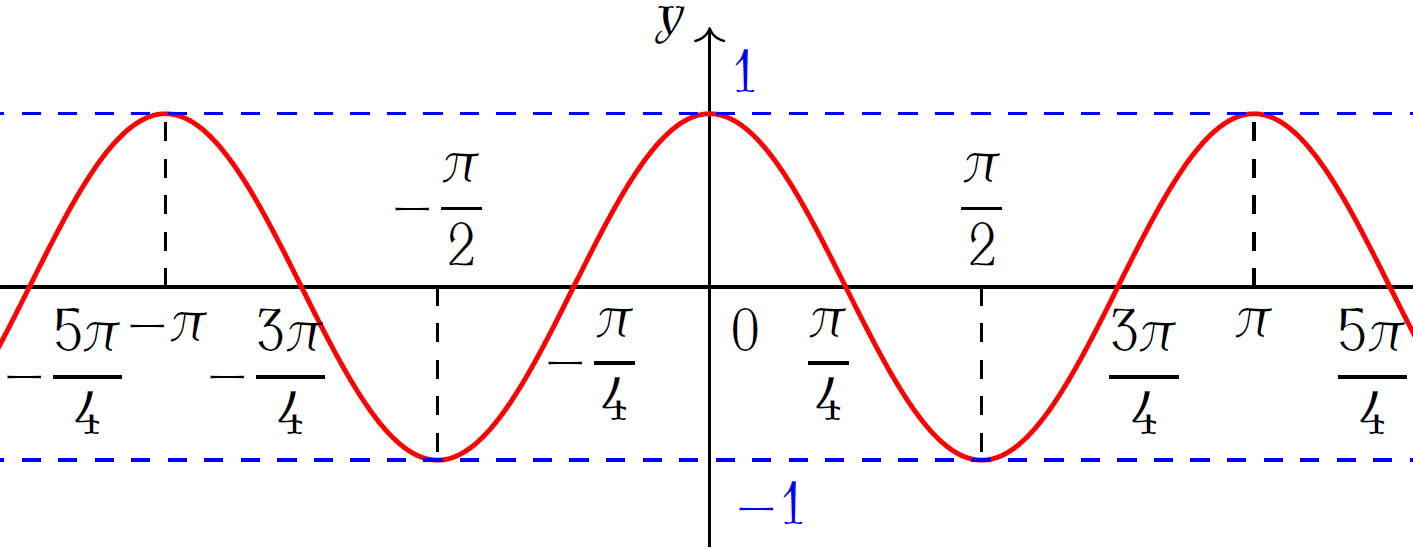
Mệnh đề nào sau đây sai?
| Trên đoạn \(\left[0;\dfrac{\pi}{4}\right]\) hàm số có giá trị lớn nhất bằng \(1\) | |
| Trên đoạn \(\left[0;\dfrac{\pi}{4}\right]\) hàm số có giá trị nhỏ nhất bằng \(-1\) | |
| Trên \(\mathbb{R}\), hàm số có giá trị lớn nhất bằng \(1\) | |
| Trên \(\mathbb{R}\), hàm số có giá trị nhỏ nhất bằng \(-1\) |
Hàm số nào sau đây có tập xác định là \(\mathscr{D}=\mathbb{R}\setminus\left\{k\pi,\,k\in\mathbb{Z}\right\}\)?
| \(y=\cot x\) | |
| \(y=\tan x\) | |
| \(y=\dfrac{1}{\sin x-1}\) | |
| \(y=\cos x\) |
Tìm tập xác định của hàm số \(y=\tan x\).
| \(\mathscr{D}=\mathbb{R}\setminus\left\{k\pi,\,k\in\mathbb{Z}\right\}\) | |
| \(\mathscr{D}=\mathbb{R}\setminus\left\{k2\pi,\,k\in\mathbb{Z}\right\}\) | |
| \(\mathscr{D}=\mathbb{R}\setminus\left\{\dfrac{\pi}{2}+k\pi,\,k\in\mathbb{Z}\right\}\) | |
| \(\mathscr{D}=\mathbb{R}\setminus\left\{\dfrac{\pi}{2}+k2\pi,\,k\in\mathbb{Z}\right\}\) |
Hàm số nào sau đây có tập xác định là \(\mathbb{R}\)?
| \(y=\tan x+\sin\dfrac{7\pi}{12}\) | |
| \(y=\dfrac{1}{\sqrt{1-\cos x}}\) | |
| \(y=\cot2x\) | |
| \(y=\sqrt{1+\sin x}+\tan\dfrac{\pi}{12}\) |
Tìm tập xác định \(\mathscr{D}\) của hàm số $$y=\sqrt{1-\sin2x}-\sqrt{1+\sin2x}$$
| \(\mathscr{D}=\mathbb{R}\) | |
| \(\mathscr{D}=\left[\dfrac{\pi}{6}+k2\pi;\dfrac{5\pi}{6}+k2\pi\right],\,k\in\mathbb{Z}\) | |
| \(\mathscr{D}=\left[\dfrac{5\pi}{6}+k2\pi;\dfrac{13\pi}{6}+k2\pi\right],\,k\in\mathbb{Z}\) | |
| \(\mathscr{D}=\varnothing\) |
Tìm tập xác định \(\mathscr{D}\) của hàm số $$y=\dfrac{1}{\sqrt{1-\sin x}}$$
| \(\mathscr{D}=\mathbb{R}\setminus\left\{k\pi,\,k\in\mathbb{Z}\right\}\) | |
| \(\mathscr{D}=\mathbb{R}\setminus\left\{\dfrac{\pi}{2}+k\pi,\,k\in\mathbb{Z}\right\}\) | |
| \(\mathscr{D}=\mathbb{R}\setminus\left\{\dfrac{\pi}{2}+k2\pi,\,k\in\mathbb{Z}\right\}\) | |
| \(\mathscr{D}=\varnothing\) |
Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\sqrt{\sin x-1}\).
| \(\mathscr{D}=\mathbb{R}\) | |
| \(\mathscr{D}=\mathbb{R}\setminus\left\{\dfrac{\pi}{2}+k2\pi,\,k\in\mathbb{Z}\right\}\) | |
| \(\mathscr{D}=\left\{\dfrac{\pi}{2}+k\pi,\,k\in\mathbb{Z}\right\}\) | |
| \(\mathscr{D}=\left\{\dfrac{\pi}{2}+k2\pi,\,k\in\mathbb{Z}\right\}\) |
Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\sqrt{\sin x-2}\).
| \(\mathscr{D}=\mathbb{R}\) | |
| \(\mathscr{D}=\left[-2;+\infty\right)\) | |
| \(\mathscr{D}=\left[0;2\pi\right]\) | |
| \(\mathscr{D}=\varnothing\) |
Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\sqrt{\sin x+2}\).
| \(\mathscr{D}=\mathbb{R}\) | |
| \(\mathscr{D}=\left[-2;+\infty\right)\) | |
| \(\mathscr{D}=\left[0;2\pi\right]\) | |
| \(\mathscr{D}=\varnothing\) |
Tìm tập xác định \(\mathscr{D}\) của hàm số $$y=\dfrac{\cot x+3}{\cos x}$$
| \(\mathscr{D}=\Bbb{R}\setminus \left\{\dfrac{k\pi}{2},\,k\in\Bbb{Z}\right\}\) | |
| \(\mathscr{D}=\Bbb{R}\setminus\left\{k\pi,\,k\in \Bbb{Z}\right\}\) | |
| \(\mathscr{D}=\Bbb{R}\setminus\left\{k2\pi,\,k\in \Bbb{Z}\right\}\) | |
| \(\mathscr{D}=\Bbb{R}\setminus\left\{\dfrac{\pi}{2}+k\pi ,\,k\in\Bbb{Z}\right\}\) |
Tìm tập xác định \(\mathscr{D}\) của hàm số $$y=\dfrac{\tan x}{1-\cos^2x}$$
| \(\mathbb{R}\setminus\left\{\dfrac{\pi}{2}+k2\pi,\,k\in\mathbb{Z}\right\}\) | |
| \(\mathbb{R}\setminus\left\{\dfrac{k\pi}{2},\,k\in\mathbb{Z}\right\}\) | |
| \(\mathbb{R}\setminus\left\{-\dfrac{\pi}{2}+k2\pi,\,k\in\mathbb{Z}\right\}\) | |
| \(\mathbb{R}\setminus\left\{k\pi,\,k\in\mathbb{Z}\right\}\) |
Tìm tập xác định \(\mathscr{D}\) của hàm số $$y=\dfrac{3\tan x-5}{1-\sin^2x}$$
| \(\mathscr{D}=\mathbb{R}\setminus\left\{\dfrac{\pi}{2}+k2\pi,\,k\in\mathbb{Z}\right\}\) | |
| \(\mathscr{D}=\mathbb{R}\setminus\left\{\dfrac{\pi}{2}+k\pi,\,k\in\mathbb{Z}\right\}\) | |
| \(\mathscr{D}=\mathbb{R}\setminus\left\{\pi+k\pi,\,k\in\mathbb{Z}\right\}\) | |
| \(\mathscr{D}=\mathbb{R}\setminus\left\{\pi+k2\pi,\,k\in\mathbb{Z}\right\}\) |
Tìm tập xác định \(\mathscr{D}\) của hàm số $$y=3\tan^2\left(\dfrac{x}{2}-\dfrac{\pi}{4}\right)$$
| \(\mathscr{D}=\mathbb{R}\setminus\left\{\dfrac{3\pi}{2}+k2\pi,\,k\in\mathbb{Z}\right\}\) | |
| \(\mathscr{D}=\mathbb{R}\setminus\left\{\dfrac{\pi}{2}+k2\pi,\,k\in\mathbb{Z}\right\}\) | |
| \(\mathscr{D}=\mathbb{R}\setminus\left\{\dfrac{3\pi}{2}+k\pi,\,k\in\mathbb{Z}\right\}\) | |
| \(\mathscr{D}=\mathbb{R}\setminus\left\{\dfrac{\pi}{2}+k\pi,\,k\in\mathbb{Z}\right\}\) |
Tìm tập xác định \(\mathscr{D}\) của hàm số $$y=\cot\left(2x-\dfrac{\pi}{4}\right)+\sin2x$$
| \(\mathscr{D}=\mathbb{R}\) | |
| \(\mathscr{D}=\varnothing\) | |
| \(\mathscr{D}=\mathbb{R}\setminus\left\{\dfrac{\pi}{8}+k\dfrac{\pi}{2},\,k\in\mathbb{Z}\right\}\) | |
| \(\mathscr{D}=\mathbb{R}\setminus\left\{\dfrac{\pi}{8}+k\pi,\,k\in\mathbb{Z}\right\}\) |
Tìm tập xác định \(\mathscr{D}\) của hàm số $$y=\dfrac{1}{\sin x-\cos x}$$
| \(\mathscr{D}=\mathbb{R}\) | |
| \(\mathscr{D}=\mathbb{R}\setminus\left\{-\dfrac{\pi}{4}+k\pi,\,k\in\mathbb{Z}\right\}\) | |
| \(\mathscr{D}=\mathbb{R}\setminus\left\{\dfrac{\pi}{4}+k2\pi,\,k\in\mathbb{Z}\right\}\) | |
| \(\mathscr{D}=\mathbb{R}\setminus\left\{\dfrac{\pi}{4}+k\pi,\,k\in\mathbb{Z}\right\}\) |
