Cho hàm số \(f(x)\) thỏa mãn \(f'(x)=x\mathrm{e}^x\) và \(f(0)=2\). Tính \(f(1)\).

	\(f(1)=8-2\mathrm{e}\)
	\(f(1)=\mathrm{e}\)
	\(f(1)=3\)
	\(f(1)=5-2\mathrm{e}\)

Họ nguyên hàm của hàm số \(f(x)=x\mathrm{e}^{2x}\) là

	\(F(x)=2\mathrm{e}^{2x}\left(x-\dfrac{1}{2}\right)+C\)
	\(F(x)=2\mathrm{e}^{2x}(x-2)+C\)
	\(F(x)=\dfrac{1}{2}\mathrm{e}^{2x}(x-2)+C\)
	\(F(x)=\dfrac{1}{2}\mathrm{e}^{2x}\left(x-\dfrac{1}{2}\right)+C\)

Cho \(F(x)\) là một nguyên hàm của hàm số \(f(x)=\dfrac{1}{2x+1}\), biết \(F(0)=2\). Tính \(F(1)\).

	\(F(1)=\dfrac{1}{2}\ln3+2\)
	\(F(1)=\ln3+2\)
	\(F(1)=2\ln3-2\)
	\(F(1)=\dfrac{1}{2}\ln3-2\)

Tìm nguyên hàm của hàm số \(f(x)=\dfrac{1}{1-2x}\) trên khoảng \(\left(-\infty;\dfrac{1}{2}\right)\).

	\(\dfrac{1}{2}\ln|2x-1|+C\)
	\(\dfrac{1}{2}\ln(1-2x)+C\)
	\(\ln|2x-1|+C\)
	\(-\dfrac{1}{2}\ln|2x-1|+C\)

Nguyên hàm của hàm số \(f(x)=\dfrac{1}{2\sqrt{2x+1}}\) có dạng

	\(\sqrt{2x+1}+C\)
	\(\dfrac{1}{(2x+1)\sqrt{2x+1}}+C\)
	\(2\sqrt{2x+1}+C\)
	\(\dfrac{1}{2}\sqrt{2x+1}+C\)

Tìm họ nguyên hàm của hàm số \(f(x)=3x-\sin x\).

	\(\displaystyle\int f(x)\mathrm{\,d}x=\dfrac{3x^2}{2}+\cos x+C\)
	\(\displaystyle\int f(x)\mathrm{\,d}x=3+\cos x+C\)
	\(\displaystyle\int f(x)\mathrm{\,d}x=\dfrac{3x^2}{2}-\cos x+C\)
	\(\displaystyle\int f(x)\mathrm{\,d}x=3x^2+\cos x+C\)

Tìm nguyên hàm của hàm số \(f(x)=x+\dfrac{1}{x}\).

	\(\displaystyle\int f(x)\mathrm{\,d}x=\ln x+\dfrac{1}{2}x^2+C\)
	\(\displaystyle\int f(x)\mathrm{\,d}x=\ln|x|+x^2+C\)
	\(\displaystyle\int f(x)\mathrm{\,d}x=\ln|x|+\dfrac{1}{2}x^2+C\)
	\(\displaystyle\int f(x)\mathrm{\,d}x=\ln x+x^2+C\)

Trong các khẳng định sau, khẳng định nào sai?

	\(\displaystyle\int\dfrac{1}{x+1}\mathrm{\,d}x=\ln|x+1|+C\) (\(\forall x\neq-1\))
	\(\displaystyle\int\cos2x\mathrm{\,d}x=\dfrac{1}{2}\sin2x+C\)
	\(\displaystyle\int\mathrm{e}^{2x}\mathrm{\,d}x=\dfrac{\mathrm{e}^{2x}}{2}+C\)
	\(\displaystyle\int2^x\mathrm{\,d}x=2^x\ln2+C\)

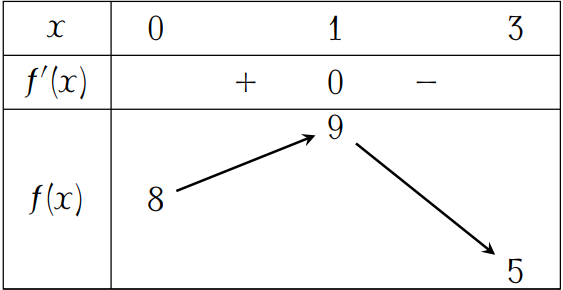
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình. Gọi \(S\) là tập hợp các số nguyên dương \(m\) để bất phương trình $$f(x)\geq mx^2\left(x^2-2\right)+2m$$có nghiệm thuộc đoạn \([0;3]\). Số phần tử của tập \(S\) là

	\(9\)
	\(10\)
	Vô số
	\(0\)

Có bao nhiêu giá trị nguyên của tham số \(m\) thuộc khoảng \((-6;5)\) sao cho phương trình $$2\cos2x+4\sin x-m\sqrt{2}=0$$vô nghiệm?

	\(3\)
	\(2\)
	\(4\)
	\(5\)

Tìm \(m\) để bất phương trình \(x+\dfrac{4}{x-1}\geq m\) có nghiệm trên khoảng \((-\infty;1)\).

	\(m\leq3\)
	\(m\leq-3\)
	\(m\leq5\)
	\(m\leq-1\)

Tiếp tuyến của đường cong \(\left(\mathscr{C}\right)\colon y=\dfrac{2x+1}{x-1}\) tại điểm \(M(2;5)\) cắt các trục tọa độ \(Ox\), \(Oy\) lần lượt tại \(A\) và \(B\). Tính diện tích tam giác \(OAB\).

	\(\dfrac{121}{6}\)
	\(\dfrac{121}{3}\)
	\(-\dfrac{121}{6}\)
	\(-\dfrac{121}{3}\)

Biết hàm số \(f(x)=\dfrac{a}{b^2\cdot3^x}\) có đồ thị đối xứng với đồ thị hàm số \(y=3^x\) qua đường thẳng \(x=-1\). Biết \(a,\,b\) là các số nguyên.

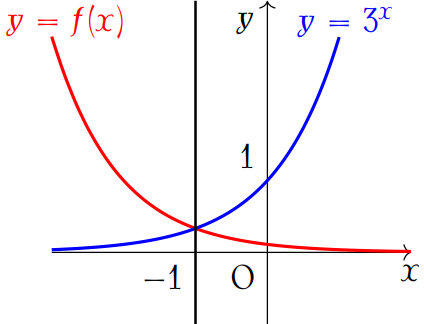
Chọn khẳng định đúng trong các khẳng định sau:

	\(b^2=9a\)
	\(b^2=4a\)
	\(b^2=6a\)
	\(b^2=a\)

Biết rằng tập hợp tất cả các giá trị thực của tham số \(m\) để hàm số $$y=\dfrac{1}{3}x^3-(m-1)x^2-(m-3)x+2020m$$đồng biến trên khoảng \((-3;-1)\) và \((0;3)\) là đoạn \(T=[a;b]\). Tính \(a^2+b^2\).

	\(a^2+b^2=8\)
	\(a^2+b^2=13\)
	\(a^2+b^2=10\)
	\(a^2+b^2=5\)

Từ một tấm bìa hình vuông \(ABCD\) có cạnh bằng \(5\)dm, người ta cắt bỏ bốn tam giác bằng nhau \(AMB\), \(BNC\), \(CPD\), \(DQA\).

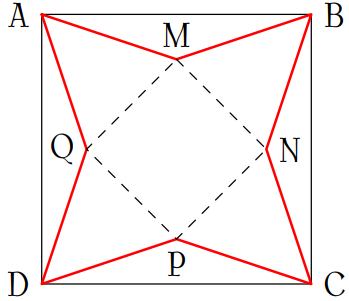
Với phần còn lại, người ta gắp lên và ghép lại để thành hình chóp tứ giác đều. Hỏi cạnh đáy của khối chóp bằng bao nhiêu để thể tích của nó là lớn nhất?

	\(\dfrac{3\sqrt{2}}{2}\)
	\(\dfrac{5}{2}\)
	\(\dfrac{5\sqrt{2}}{2}\)
	\(2\sqrt{2}\)

Gọi \(m\) là giá trị nhỏ nhất của hàm số \(y=x+\dfrac{4}{x}\) trên khoảng \((0;+\infty)\). Tìm \(m\).

	\(m=2\)
	\(m=3\)
	\(m=1\)
	\(m=4\)

Hàm số nào sau đây đồng biến trên \(\mathbb{R}\)?

	\(y=\dfrac{x-1}{x+1}\)
	\(y=\log_2x\)
	\(y=3^x\)
	\(y=x^4+2x^2+4\)

Tìm đạo hàm của hàm số \(y=\log_2(2x+1)\).

	\(y'=\dfrac{1}{2x+1}\)
	\(y'=\dfrac{1}{(2x+1)\ln2}\)
	\(y'=\dfrac{2}{(2x+1)\ln2}\)
	\(y'=\dfrac{2}{2x+1}\)

Tìm tất cả giá trị của tham số \(m\) để hàm số $$y=x^3+2x^2-mx+1$$đồng biến trên \(\mathbb{R}\).

	\(m\leq-\dfrac{4}{3}\)
	\(m\geq-\dfrac{4}{3}\)
	\(m<-\dfrac{4}{3}\)
	\(m>-\dfrac{4}{3}\)

Tập hợp các giá trị \(m\) để đồ thị hàm số \(y=\dfrac{mx^2+6x-2}{x+2}\) có tiệm cận đứng là

	\(\left\{\dfrac{7}{2}\right\}\)
	\(\mathbb{R}\setminus\left\{-\dfrac{7}{2}\right\}\)
	\(\mathbb{R}\)
	\(\mathbb{R}\setminus\left\{\dfrac{7}{2}\right\}\)