Nếu ba kích thước của một khối hộp chữ nhật tăng lên $3$ lần thì thể tích của nó tăng lên bao nhiêu lần?
| $3$ lần | |
| $9$ lần | |
| $18$ lần | |
| $27$ lần |
Cho khối lăng trụ có diện tích đáy là $30a^2$ và thể tích là $150a^3$. Tính theo $a$ khoảng cách giữa hai mặt phẳng đáy của khối lăng trụ đã cho.
| $h=5$ | |
| $h=5a$ | |
| $h=\dfrac{a}{5}$ | |
| $h=15a$ |
Cho khối chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $2a\sqrt{3}$ và $SA$ vuông góc với mặt phẳng $(ABC)$. Biết rằng thể tích của khối chóp $S.ABC$ bằng $\sqrt{3}a^3$. Tính độ dài cạnh $SA$.
| $2a\sqrt{3}$ | |
| $\sqrt{3}$ | |
| $2a$ | |
| $a$ |
Cho khối chóp $S.ABC$ có đáy là tam giác đều cạnh $2a$ và thể tích bằng $a^3$. Tính chiều cao $h$ của hình chóp đã cho.
| $h=\dfrac{\sqrt{3}a}{6}$ | |
| $h=\dfrac{\sqrt{3}a}{2}$ | |
| $h=\dfrac{\sqrt{3}a}{3}$ | |
| $h=\sqrt{3}a$ |
Cho khối chóp $S.ABC$ có đáy $ABC$ là tam giác đều, $SA$ vuông góc với mặt phẳng $(ABC)$ và $SA=a$. Biết rằng thể tích của khối chóp $S.ABC$ bằng $\sqrt{3}a^3$. Tính độ dài cạnh đáy của khối chóp $S.ABC$.
| $2a\sqrt{3}$ | |
| $3a\sqrt{3}$ | |
| $2a$ | |
| $2a\sqrt{2}$ |
Cho hình chóp tứ giác $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, $SA\perp(ABCD)$ và $SA=a\sqrt{6}$. Thể tích của khối chóp $S.ABCD$ bằng
| $a^3\sqrt{6}$ | |
| $a^3\dfrac{\sqrt{6}}{3}$ | |
| $a^3\dfrac{\sqrt{6}}{6}$ | |
| $a^3\dfrac{\sqrt{6}}{2}$ |
Cho khối chóp có diện tích đáy $B=a^2\sqrt{2}$ và chiều cao $h=2a$. Thể tích $V$ của khối chóp là
| $V=\dfrac{2a^3\sqrt{2}}{3}$ | |
| $V=\dfrac{2a^3\sqrt{2}}{9}$ | |
| $V=2a^3\sqrt{2}$ | |
| $V=\dfrac{a^3\sqrt{2}}{3}$ |
Thể tích của khối chóp có chiều cao $h=a$ và diện tích đáy $S=3a^2$ là
| $V=\dfrac{1}{3}a^3$ | |
| $V=a^3$ | |
| $V=3a^3$ | |
| $V=\dfrac{1}{6}a^3$ |
Thể tích của khối lập phương cạnh $2a$ bằng
| $8a^3$ | |
| $2a^3$ | |
| $a^3$ | |
| $6a^3$ |
Cho khối lăng trụ có thể tích bằng $V$. Biết diện tích đáy của lăng trụ là $B$, tính chiều cao $h$ của khối lăng trụ đã cho.
| $h=\dfrac{V}{3B}$ | |
| $h=\dfrac{2V}{B}$ | |
| $h=\dfrac{3V}{B}$ | |
| $h=\dfrac{V}{B}$ |
Thể tích $V$ của khối chóp có diện tích đáy $B$ và chiều cao $h$ là
| $V=\dfrac{1}{3}Bh$ | |
| $V=3Bh$ | |
| $V=\dfrac{1}{2}Bh$ | |
| $V=Bh$ |
Thể tích $V$ của khối lăng trụ có chiều cao $h$ và diện tích đáy $B$ là
| $V=Bh$ | |
| $V=\dfrac{1}{2}Bh$ | |
| $V=\dfrac{1}{6}Bh$ | |
| $V=\dfrac{1}{3}Bh$ |
Cắt khối lăng trụ $ABC.A'B'C'$ bởi mặt phẳng $\left(A'BC\right)$ ta được
| Một khối chóp tam giác và một khối chóp ngũ giác | |
| Hai khối chóp tứ giác | |
| Một khối chóp tam giác và một khối chóp tứ giác | |
| Hai khối chóp tam giác |
Cho khối lập phương $ABCD.A'B'C'D'$. Mặt phẳng $\left(BDD'B'\right)$ chia khối lập phương thành
| Hai khối lăng trụ tam giác | |
| Hai khối tứ diện | |
| Hai khối lăng trụ tứ giác | |
| Hai khối chóp tứ giác |
Có thể chia khối chóp $S.ABCD$ thành hai khối tứ diện là
| $SBCD$ và $SACD$ | |
| $SACD$ và $SABD$ | |
| $SABC$ và $SABD$ | |
| $SABC$ và $SACD$ |
Cho khối chóp có đáy là đa giác $n$ cạnh. Mệnhh đề nào sau đây là đúng?
| Số mặt của khối chóp là $2n$ | |
| Số đỉnh của khối chóp bằng $2n+1$ | |
| Số cạnh của khối chóp bằng $n+1$ | |
| Số mặt của khối chóp bằng số đỉnh của nó |
Hình lăng trụ có thể có số cạnh là số nào sau đây?
| $3000$ | |
| $3001$ | |
| $3005$ | |
| $3007$ |
Trong các hình dưới đây, hình nào không phải hình đa diện?
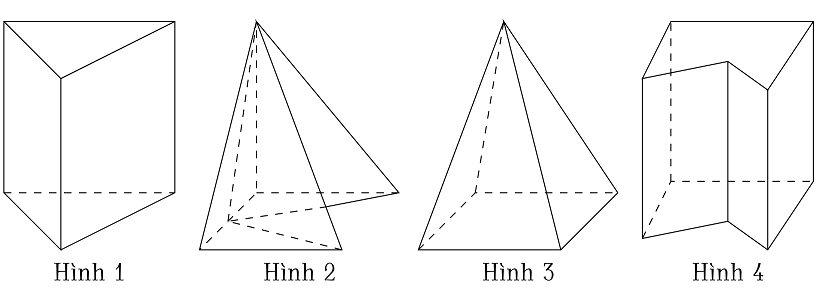
| Hình 1 | |
| Hình 2 | |
| Hình 3 | |
| Hình 4 |
Trong các hình dưới đây, hình nào không phải hình đa diện?
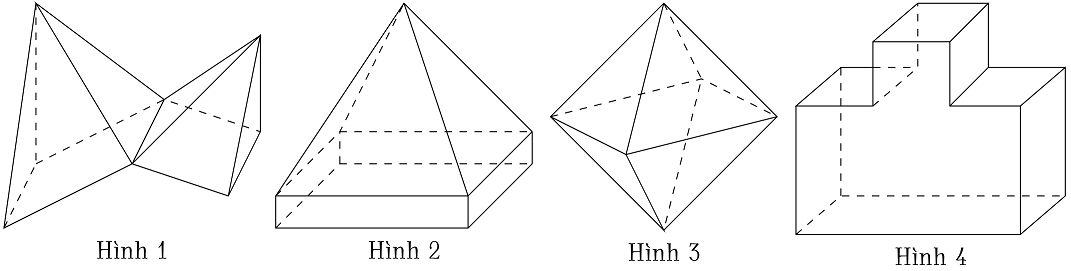
| Hình 1 | |
| Hình 2 | |
| Hình 3 | |
| Hình 4 |
Trong các hình dưới đây, hình nào là hình đa diện?
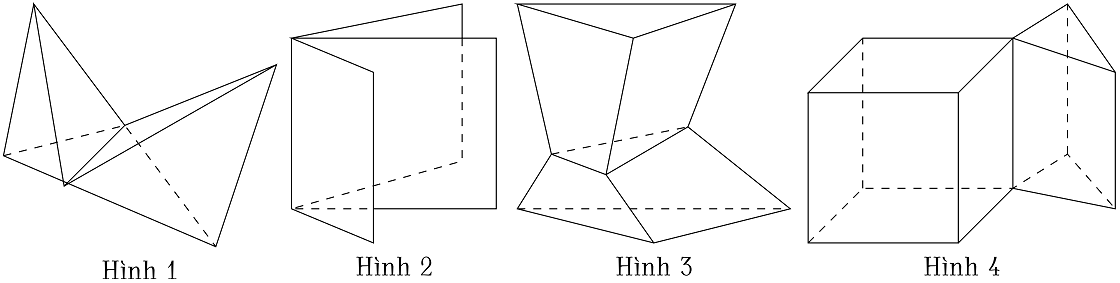
| Hình 4 | |
| Hình 2 | |
| Hình 1 | |
| Hình 3 |
