Cho tam giác \(ABC\) đều, cạnh \(a\), có \(I,\,J,\,K\) lần lượt là trung điểm các cạnh \(BC,\,CA,\,AB\). Tính giá trị của $$\left|\overrightarrow{AI}+\overrightarrow{BJ}+\overrightarrow{CK}\right|.$$
| \(3a\) | |
| \(\dfrac{3a\sqrt{3}}{2}\) | |
| \(0\) | |
| \(\dfrac{a\sqrt{3}}{2}\) |
Cho tam giác \(ABC\), trung tuyến \(AM\). Đẳng thức nào sau đây không đúng?
| \(\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{0}\) | |
| \(\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{0}\) | |
| \(\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AM}\) | |
| \(\overrightarrow{MB}-\overrightarrow{MC}=\overrightarrow{CB}\) |
Biết \(G\) là trọng tâm tam giác \(ABC\). Mệnh đề nào sau đây đúng?
| \(\overrightarrow{AG}+\overrightarrow{BG}=\overrightarrow{CG}\) | |
| \(\overrightarrow{GA}+\overrightarrow{GB}=\overrightarrow{CG}\) | |
| \(\overrightarrow{GA}-\overrightarrow{GB}=\overrightarrow{CG}\) | |
| \(\overrightarrow{GA}-\overrightarrow{GB}=\overrightarrow{GC}\) |
Cho tam giác \(ABC\) có trọng tâm \(G\), \(M\) là trung điểm cạnh \(BC\). Mệnh đề nào sau đây sai?
| \(\overrightarrow{MB}+\overrightarrow{MC}=\vec{0}\) | |
| \(\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AM}\) | |
| \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\vec{0}\) | |
| \(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=-3\overrightarrow{MG}\) |
Cho tam giác \(ABC\) có \(G\) là trọng tâm. Mệnh đề nào sau đây sai?
| \(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}\) | |
| \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\vec{0}\) | |
| \(\overrightarrow{GB}+\overrightarrow{GC}=2\overrightarrow{GA}\) | |
| \(3\overrightarrow{AG}=\overrightarrow{AB}+\overrightarrow{AC}\) |
Gọi \(M\) là trung điểm của đoạn thẳng \(AB\). Khẳng định nào sau đây là sai?
| \(\overrightarrow{AB}=2\overrightarrow{MB}\) | |
| \(\overrightarrow{MA}+\overrightarrow{MB}=\vec{0}\) | |
| \(\overrightarrow{MA}=-\dfrac{1}{2}\overrightarrow{AB}\) | |
| \(\overrightarrow{MA}=\overrightarrow{MB}\) |
Cho hình bình hành \(ABCD\), tâm \(M\). Mệnh đề nào sau đây sai?
| \(\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\) | |
| \(\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}\) | |
| \(\overrightarrow{BA}+\overrightarrow{BC}=2\overrightarrow{BM}\) | |
| \(\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{MC}+\overrightarrow{MD}\) |
Cho hình bình hành \(ABCD\). Đẳng thức nào sau đây đúng?
| \(\overrightarrow{AC}+\overrightarrow{BD}=2\overrightarrow{BC}\) | |
| \(\overrightarrow{AC}+\overrightarrow{BD}=\overrightarrow{AB}\) | |
| \(\overrightarrow{AC}-\overrightarrow{BD}=2\overrightarrow{CD}\) | |
| \(\overrightarrow{AC}-\overrightarrow{AD}=\overrightarrow{CD}\) |
Cho tam giác \(ABC\). Gọi \(M,\,N\) lần lượt là trung điểm của \(AB\) và \(AC\). Khẳng định nào sau đây sai?
| \(\overrightarrow{AB}=2\overrightarrow{AM}\) | |
| \(\overrightarrow{AC}=2\overrightarrow{NC}\) | |
| \(\overrightarrow{CB}=-2\overrightarrow{MN}\) | |
| \(\overrightarrow{CN}=-\dfrac{1}{2}\overrightarrow{AC}\) |
Cho tam giác \(ABC\) có \(G\) là trọng tâm và \(I\) là trung điểm cạnh \(BC\). Đẳng thức nào sau đây đúng?
| \(\overrightarrow{GA}=2\overrightarrow{GI}\) | |
| \(\overrightarrow{IG}=-\dfrac{1}{3}\overrightarrow{IA}\) | |
| \(\overrightarrow{GB}+\overrightarrow{GC}=2\overrightarrow{GI}\) | |
| \(\overrightarrow{GB}+\overrightarrow{GC}=2\overrightarrow{GA}\) |
Cho tam giác \(ABC\) có \(M\) là trung điểm của \(BC\), \(G\) là trọng tâm. Khẳng định nào sau đây đúng?
| \(\overrightarrow{AG}=\dfrac{2}{3}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\) | |
| \(\overrightarrow{AG}=\dfrac{1}{3}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\) | |
| \(\overrightarrow{AG}=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}\) | |
| \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AB}+3\dfrac{1}{2}\overrightarrow{AC}\) |
Cho tam giác \(ABC\) có \(M\) là trung điểm của \(BC\), \(I\) là trung điểm của \(AM\). Khẳng định nào sau đây đúng?
| \(\overrightarrow{AI}=\dfrac{1}{4}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\) | |
| \(\overrightarrow{AI}=\dfrac{1}{4}\left(\overrightarrow{AB}-\overrightarrow{AC}\right)\) | |
| \(\overrightarrow{AI}=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\) | |
| \(\overrightarrow{AI}=\dfrac{1}{4}\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AC}\) |
Cho tam giác \(ABC\) có \(M\) là trung điểm của \(BC\), \(I\) là trung điểm của \(AM\). Khẳng định nào sau đây đúng?
| \(\overrightarrow{IB}+2\overrightarrow{IC}+\overrightarrow{IA}=\vec{0}\) | |
| \(\overrightarrow{IB}+\overrightarrow{IC}+2\overrightarrow{IA}=\vec{0}\) | |
| \(2\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{IA}=\vec{0}\) | |
| \(\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{IA}=\vec{0}\) |
Cho tam giác \(OAB\) vuông cân tại \(O\), cạnh \(OA=a\). Tính \(\left|2\overrightarrow{OA}-\overrightarrow{OB}\right|\).
| \(a\) | |
| \(\left(1+\sqrt{2}\right)a\) | |
| \(a\sqrt{5}\) | |
| \(2a\sqrt{2}\) |
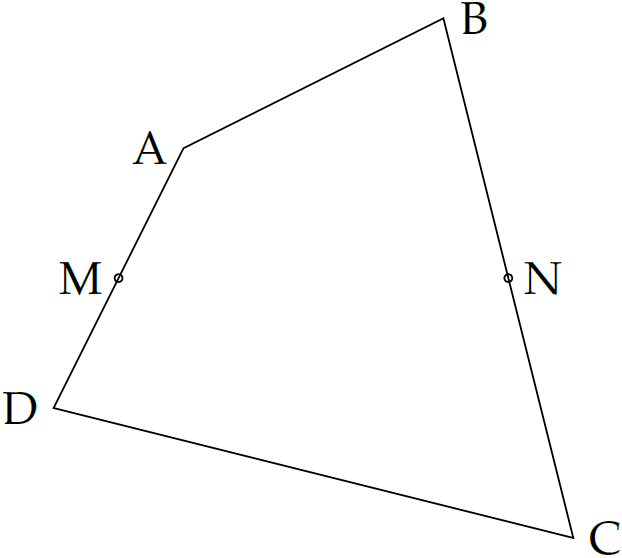
Bạn Thùy đặt một tấm bìa cứng hình tứ giác (như hình vẽ) lên đầu một ngòi bút nhưng tấm bìa không bị rơi. Hỏi bạn Thùy đã đặt ngòi bút tại điểm nào của tấm bìa?
| Trung điểm của \(MN\) | |
| Trung điểm \(M\) | |
| Trung điểm \(N\) | |
| Giao điểm \(AC\) và \(BD\) |
Người ta dùng hai sợi dây chắc chắn buộc vào một vật. Một đầu dây buộc vào \(3\) chiếc xe con nối đuôi nhau, một đầu dây còn lại buộc vào \(2\) chiếc xe tải nối đuôi nhau. Hai đoàn xe chạy về hai hướng ngược nhau nhưng kết quả là vật vẫn đứng yên, không dịch về phía nào. Hỏi, nếu lực kéo của mỗi chiếc xe con là \(100\)N thì lực kéo của mỗi chiếc xe tải là bao nhiêu?
| \(100\)N | |
| \(150\)N | |
| \(200\)N | |
| \(300\)N |
Cho hình thoi \(ABCD\) có \(AC=2a\) và \(BD=a\). Tính \(\left|\overrightarrow{AC}+\overrightarrow{BD}\right|\).
| \(\left|\overrightarrow{AC}+\overrightarrow{BD}\right|=3a\) | |
| \(\left|\overrightarrow{AC}+\overrightarrow{BD}\right|=a\sqrt{3}\) | |
| \(\left|\overrightarrow{AC}+\overrightarrow{BD}\right|=a\sqrt{5}\) | |
| \(\left|\overrightarrow{AC}+\overrightarrow{BD}\right|=5a\) |
Cho tam giác \(ABC\) cân tại \(A\), đường cao \(AH\). Khẳng định nào sau đây sai?
| \(\overrightarrow{AB}=\overrightarrow{AC}\) | |
| \(\overrightarrow{HC}=-\overrightarrow{HB}\) | |
| \(\left|\overrightarrow{AB}\right|=\left|\overrightarrow{AC}\right|\) | |
| \(\overrightarrow{BC}=2\overrightarrow{HC}\) |
Vectơ đối của vectơ \(5\vec{a}-3\vec{b}\) là
| \(5\vec{a}+3\vec{b}\) | |
| \(-5\vec{a}+3\vec{b}\) | |
| \(-5\vec{a}-3\vec{b}\) | |
| \(3\vec{a}-5\vec{b}\) |
Vectơ đối của vectơ \(5\overrightarrow{u}\) là
| \(\overrightarrow{u}-5\) | |
| \(-\overrightarrow{u}\) | |
| \(5-\overrightarrow{u}\) | |
| \(-5\overrightarrow{u}\) |
