Phát biểu nào sau đây là sai?

	Vectơ là đoạn thẳng có hướng
	Hai vectơ cùng hướng thì cùng phương
	Vectơ \(\vec{0}\) cùng phương với mọi vectơ
	Hai vectơ cùng phương thì cùng hướng

Tứ giác \(ABCD\) là hình bình hành khi và chỉ khi

	\(\overrightarrow{AC}=\overrightarrow{BD}\)
	\(\overrightarrow{BC}=\overrightarrow{DA}\)
	\(\overrightarrow{BA}=\overrightarrow{CD}\)
	\(\overrightarrow{AB}=\overrightarrow{CD}\)

Cho bốn điểm phân biệt \(A,\,B,\,C,\,D\) mà trong đó không có ba điểm nào thẳng hàng. Điều kiện cần và đủ để \(\overrightarrow{AB}=\overrightarrow{CD}\) là

	\(ABCD\) là hình bình hành
	\(ABDC\) là hình bình hành
	\(AC=BD\)
	\(AB=CD\)

Hai vectơ được gọi là bằng nhau khi và chỉ khi

	Giá của chúng trùng nhau và độ dài của chúng bằng nhau
	Chúng trùng với một trong các cặp cạnh đối của một hình bình hành
	Chúng trùng với một trong các cặp cạnh đối của một tam giác đều
	Chúng cùng hướng và độ dài bằng nhau

Mệnh đề nào sau đây sai?

	\(\overrightarrow{AA}=\vec{0}\)
	\(\vec{0}\) cùng hướng với mọi vectơ
	\(\left|\overrightarrow{AB}\right|>0\)
	\(\vec{0}\) cùng phương với mọi vectơ

Cho vectơ \(\overrightarrow{DE}\) khác \(\vec{0}\). Độ dài đoạn thẳng \(ED\) được gọi là

	Phương của \(\overrightarrow{ED}\)
	Hướng của \(\overrightarrow{ED}\)
	Giá của \(\overrightarrow{ED}\)
	Độ dài của \(\overrightarrow{ED}\)

Cho ba điểm \(A,\,B,\,C\) phân biệt. Khi đó

	Điều kiện cần và đủ để \(A,\,B,\,C\) thẳng hàng là \(\overrightarrow{AB}\) cùng phương với \(\overrightarrow{AC}\)
	Điều kiện đủ để \(A,\,B,\,C\) thẳng hàng là \(\overrightarrow{MA}\) cùng phương với \(\overrightarrow{AB}\) với mọi \(M\)
	Điều kiện cần để \(A,\,B,\,C\) thẳng hàng là \(\overrightarrow{MA}\) cùng phương với \(\overrightarrow{AB}\) vói mọi \(M\)
	Điều kiện cần để \(A,\,B,\,C\) thẳng hàng là \(\overrightarrow{AB}=\overrightarrow{AC}\)

Mệnh đề nào sau đây đúng?

	Có duy nhất một vectơ cùng phương với mọi vectơ
	Có ít nhất hai vectơ có cùng phương với mọi vectơ
	Có vô số vectơ cùng phương với mọi vectơ
	Không có vectơ nào cùng phương với mọi vectơ

Cho tứ giác \(ABCD\). Có bao nhiêu vectơ khác \(\vec{0}\) có điểm đầu và điểm cuối là các đỉnh của tứ giác?

	\(4\)
	\(6\)
	\(8\)
	\(12\)

Từ ba điểm \(A,\,B,\,C\) phân biệt, có thể lập được bao nhiêu vectơ (khác vectơ \(\vec{0}\)) có điểm đầu, điểm cuối là hai trong ba điểm đã cho?

	\(3\)
	\(4\)
	\(5\)
	\(6\)

Cho vectơ \(\vec{a}\). Có bao nhiêu vectơ bằng với \(\vec{a}\)?

	Vô số
	Duy nhất
	Không tồn tại
	\(2\)

Từ hai điểm \(A,\,B\) phân biệt có thể lập được bao nhiêu vectơ?

	\(2\)
	\(1\)
	\(4\)
	\(3\)

Vectơ có điểm đầu \(A\) và điểm cuối \(B\) được ký hiệu là

	\(AB\)
	\(\overline{AB}\)
	\(\overrightarrow{BA}\)
	\(\overrightarrow{AB}\)

Cho các hàm số \(y=\log_ax\),  \(y=b^x\), \(y=c^x\) có đồ thị như hình vẽ.

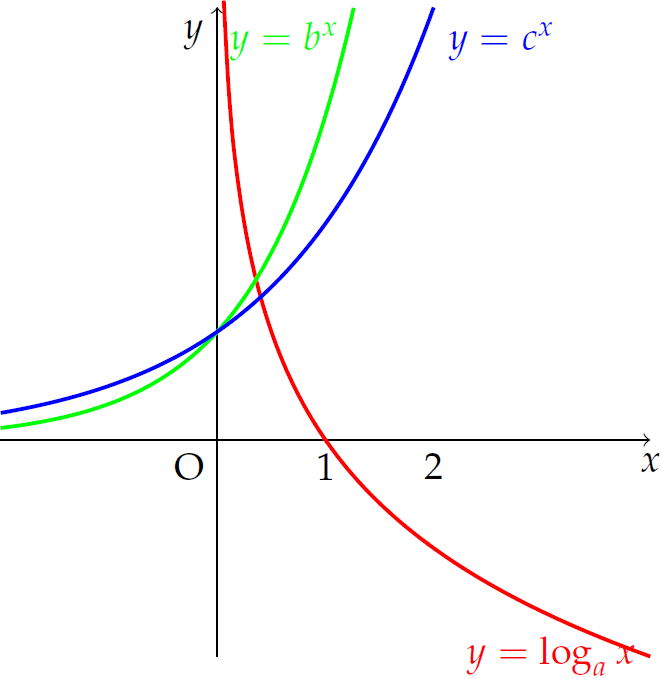
Mệnh đề nào dưới đây là đúng?

	\(b>c>a\)
	\(a>b>c\)
	\(b>a>c\)
	\(c>b>a\)

Hình vẽ bên biểu diễn đồ thị của hai hàm số \(y=a^x\) và \(y=\log_bx\) với \(a,\,b\) là các số thực dương và \(b\neq1\).

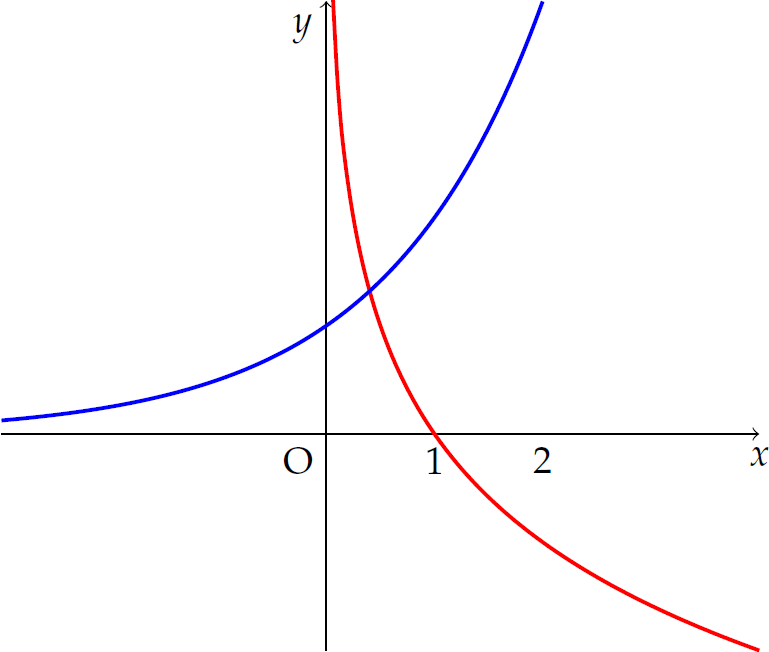
Mệnh đề nào dưới đây là đúng?

	\(\log_ab^2>0\)
	\(\log_ab<0\)
	\(\log_ab>0\)
	\(\log_ba>0\)

Cho ba số thực dương \(a,\,b,\,c\) khác \(1\). Đồ thị hàm số \(y=a^x\), \(y=b^x\) và \(y=c^x\) được cho trong hình vẽ.

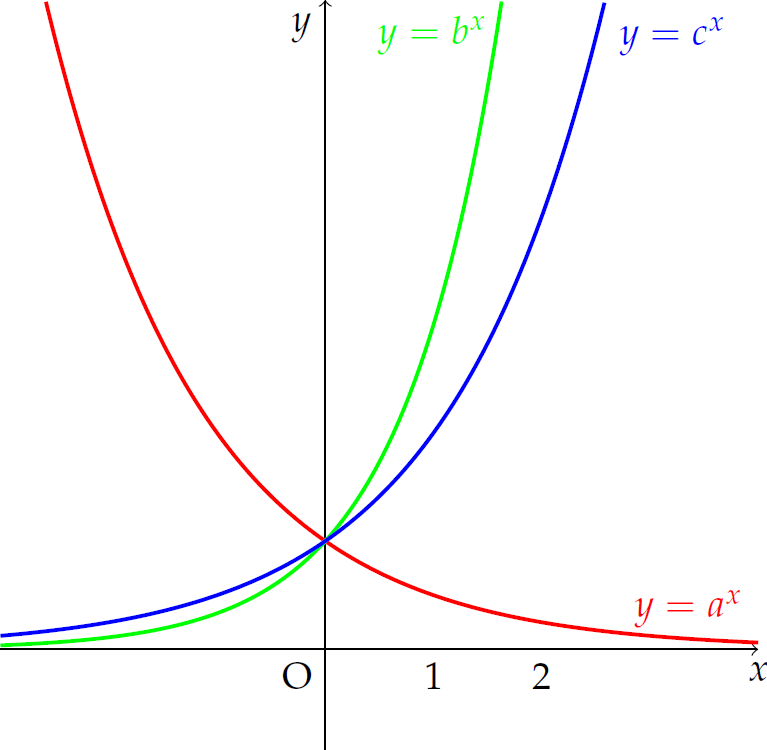
Mệnh đề nào dưới đây là đúng?

	\(a< b< c\)
	\(a< c< b\)
	\(b< c< a\)
	\(c< a< b\)

Cho \(a,\,b,\,c\) dương và khác \(1\). Đồ thị hàm số \(y=\log_ax\), \(y=\log_bx\) và \(y=\log_cx\) được cho trong hình vẽ.

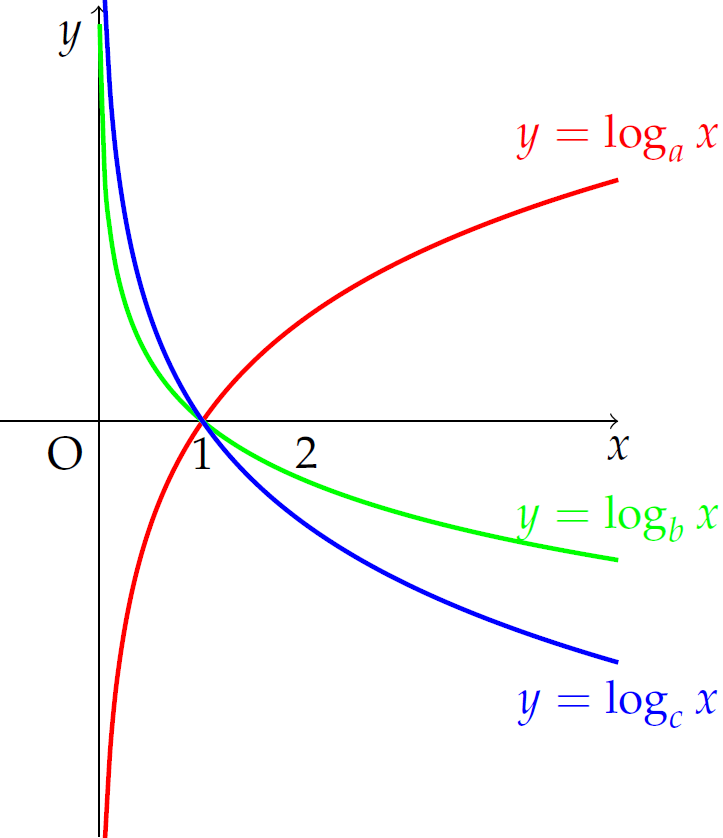
Khẳng định nào dưới đây là đúng?

	\(a>c>b\)
	\(b>c>a\)
	\(c>b>a\)
	\(a>b>c\)

Số điểm cực trị của hàm số \(y=\mathrm{e}^x+x+1\) là

	\(0\)
	\(3\)
	\(2\)
	\(1\)

Tìm các khoảng đồng biến của hàm số $$y=2^{x^2-6x+5}$$

	\((-\infty;3)\)
	\(\mathbb{R}\)
	\((3;+\infty)\)
	\((-\infty;1)\) và \((5;+\infty)\)

Trong các hàm số dưới đây, hàm số nào nghịch biến trên \(\mathbb{R}\)?

	\(y=\left(\dfrac{\pi}{3}\right)^x\)
	\(y=\log_{\tfrac{\pi}{4}}\left(2x^2+1\right)\)
	\(y=\left(\dfrac{2}{\mathrm{e}}\right)^x\)
	\(y=\log_{\tfrac{2}{3}}x\)