Hàm số \(y=x^3-3x^2+5\) đồng biến trên khoảng
| \((0;2)\) | |
| \((0;+\infty)\) | |
| \((-\infty;2)\) | |
| \((-\infty;0)\) và \((2;+\infty)\) |
Hàm số \(y=x^3+3x^2-4\) nghịch biến trên khoảng
| \((-\infty;-2)\) | |
| \((0;+\infty)\) | |
| \((-2;+\infty)\) | |
| \((-2;0)\) |
Hàm số \(y=\dfrac{x^3}{3}-\dfrac{x^2}{2}-6x+\dfrac{3}{4}\)
| Đồng biến trên khoảng \((-2;3)\) | |
| Nghịch biến trên khoảng \((-2;3)\) | |
| Nghịch biến trên khoảng \((-\infty;-2)\) | |
| Đồng biến trên khoảng \((-2;+\infty)\) |
Mệnh đề nào sau đây là đúng?
| Hàm số \(y=f(x)\) đồng biến trên khoảng \((a;b)\) khi và chỉ khi \(f'(x)\geq0,\;\forall x\in(a;b)\) | |
| Nếu \(f'(x)\geq0,\;\forall x\in(a;b)\) thì hàm số \(y=f(x)\) đồng biến trên khoảng \((a;b)\) | |
| Hàm số \(y=f(x)\) đồng biến trên khoảng \((a;b)\) khi và chỉ khi \(f'(x)>0,\;\forall x\in(a;b)\) | |
| Nếu \(f'(x)>0,\;\forall x\in(a;b)\) thì hàm số \(y=f(x)\) đồng biến trên khoảng \((a;b)\) |
Tính thể tích \(V\) của vật tròn xoay tạo thành khi quay hình phẳng \((H)\) giới hạn bởi các đường \(y=x^2\) và \(y=\sqrt{x}\) quanh trục \(Ox\).
| \(V=\dfrac{3\pi}{10}\) | |
| \(V=\dfrac{\pi}{10}\) | |
| \(V=\dfrac{7\pi}{10}\) | |
| \(V=\dfrac{9\pi}{10}\) |
Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường \(y=x^2-2x\), \(y=0\), \(x=0\), \(x=1\) quanh trục hoành là
| \(\dfrac{8\pi}{15}\) | |
| \(\dfrac{7\pi}{3}\) | |
| \(\dfrac{15\pi}{8}\) | |
| \(\dfrac{8\pi}{7}\) |
Tìm công thức tính thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi parabol \((P)\colon y=x^2\) và đường thẳng \(d\colon y=2x\) quay quanh trục \(Ox\).
| \(\pi\displaystyle\int\limits_{0}^{2}\left(x^2-2x\right)^2\mathrm{\,d}x\) | |
| \(\pi\displaystyle\int\limits_{0}^{2}4x^2\mathrm{\,d}x-\pi\displaystyle\int\limits_{0}^{2}x^4\mathrm{\,d}x\) | |
| \(\pi\displaystyle\int\limits_{0}^{2}4x^2\mathrm{\,d}x+\pi\displaystyle\int\limits_{0}^{2}x^4\mathrm{\,d}x\) | |
| \(\pi\displaystyle\int\limits_{0}^{2}\left(2x-x^2\right)\mathrm{\,d}x\) |
Gọi \((H)\) là hình phẳng tạo bởi đồ thị hàm số \(y=\sqrt{x^3-x^2-2x}\) và trục hoành. Khi cho \((H)\) quay quanh trục hoành, ta được khối tròn xoay có thể tích là
| \(\dfrac{13\pi}{6}\) | |
| \(\dfrac{9\pi}{4}\) | |
| \(\dfrac{5\pi}{12}\) | |
| \(\dfrac{8\pi}{3}\) |
Cho hình phẳng \(D\) giới hạn bởi đường cong \(y=\mathrm{e}^x\), trục hoành và các đường thẳng \(x=0\), \(x=1\). Khối tròn xoay tạo thành khi quay \(D\) quanh trục hoành có thể tích \(V\) bằng
| \(V=\dfrac{\mathrm{e}^2-1}{2}\) | |
| \(V=\dfrac{\pi\left(\mathrm{e}^2+1\right)}{2}\) | |
| \(V=\dfrac{\pi\left(\mathrm{e}^2-1\right)}{2}\) | |
| \(V=\dfrac{\pi\mathrm{e}^2}{2}\) |
Cho hình phẳng giới hạn bởi đồ thị các hàm số \(y=\sqrt{x}\), đường thẳng \(y=2-x\) và trục hoành (phần gạch chéo trong hình vẽ).
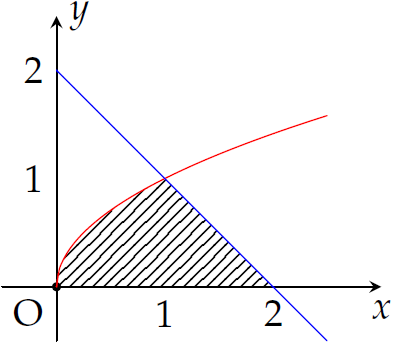
Thể tích của khối tròn xoay sinh bởi hình phẳng trên khi quay quanh trục \(Ox\) bằng
| \(\dfrac{5\pi}{4}\) | |
| \(\dfrac{4\pi}{3}\) | |
| \(\dfrac{7\pi}{6}\) | |
| \(\dfrac{5\pi}{6}\) |
Gọi \((H)\) là hình phẳng giới hạn bởi đồ thị \((C)\colon y=\dfrac{4}{x}\) và đường thẳng \((d)\colon y=5-x\). Tính thể tích \(V\) của khối tròn xoay tạo thành khi quay hình \((H)\) xung quanh trục hoành.
| \(V=51\pi\) | |
| \(V=33\pi\) | |
| \(V=9\pi\) | |
| \(V=18\pi\) |
Cho hình phẳng \(D\) giới hạn bởi đường cong \(y=\sqrt{2+\cos x}\), trục hoành và các đường thẳng \(x=0\), \(x=\dfrac{\pi}{2}\). Tính thể tích \(V\) của khối tròn xoay tạo thành khi quay \(D\) quanh trục hoành.
| \(V=\pi-1\) | |
| \(V=\pi+1\) | |
| \(V=\pi(\pi-1)\) | |
| \(V=\pi(\pi+1)\) |
Gọi \(V\) là thể tích của khối tròn xoay thu được khi quay hình thang cong giới hạn bởi đồ thị hàm số \(y=\sin x\), trục \(Ox\), trục \(Oy\) và đường thẳng \(x=\dfrac{\pi}{2}\) xung quanh trục \(Ox\). Mệnh đề nào dưới đây đúng?
| \(V=\displaystyle\int\limits_{0}^{\tfrac{\pi}{2}}\sin^2x\mathrm{\,d}x\) | |
| \(V=\displaystyle\int\limits_{0}^{\tfrac{\pi}{2}}\sin x\mathrm{\,d}x\) | |
| \(V=\pi\displaystyle\int\limits_{0}^{\tfrac{\pi}{2}}\sin^2x\mathrm{\,d}x\) | |
| \(V=\pi\displaystyle\int\limits_{0}^{\tfrac{\pi}{2}}\sin x\mathrm{\,d}x\) |
Gọi \((H)\) là hình phẳng giới hạn bởi các đường \(y=4^x\), \(y=0\), \(x=1\) và \(x=3\). Thể tích \(V\) của khối tròn xoay tạo thành khi quay \((H)\) quanh trục \(Ox\) được xác định bởi công thức
| \(V=\pi\displaystyle\int\limits_{1}^{3}4^{2x}\mathrm{\,d}x\) | |
| \(V=\displaystyle\int\limits_{1}^{3}4^{x+1}\mathrm{\,d}x\) | |
| \(V=\pi\displaystyle\int\limits_{1}^{3}4^{2x+1}\mathrm{\,d}x\) | |
| \(V=\displaystyle\int\limits_{1}^{3}16^x\mathrm{\,d}x\) |
Gọi \((H)\) là hình phẳng giới hạn bởi các đường \(y=3^x\), \(y=0\), \(x=0\) và \(x=3\). Thể tích \(V\) của khối tròn xoay tạo thành khi quay \((H)\) quanh trục \(Ox\) được xác định bởi công thức
| \(V=\pi\displaystyle\int\limits_{0}^{3}3^{x+1}\mathrm{\,d}x\) | |
| \(V=\displaystyle\int\limits_{0}^{3}3^{x+1}\mathrm{\,d}x\) | |
| \(V=\pi\displaystyle\int\limits_{0}^{3}9^x\mathrm{\,d}x\) | |
| \(V=\displaystyle\int\limits_{0}^{3}9^x\mathrm{\,d}x\) |
Cho hình phẳng \((H)\) giới hạn bởi các đường \(y=x^2+3\), \(y=0\), \(x=0\), \(x=2\). Gọi \(V\) là thể tích của khối tròn xoay được tạo thành khi quay \((H)\) xung quanh trục \(Ox\). Mệnh đề nào dưới đây đúng?
| \(V=\pi\displaystyle\int\limits_{0}^{2}\left(x^2+3\right)^2\mathrm{\,d}x\) | |
| \(V=\pi\displaystyle\int\limits_{0}^{2}\left(x^2+3\right)\mathrm{\,d}x\) | |
| \(V=\displaystyle\int\limits_{0}^{2}\left(x^2+3\right)^2\mathrm{\,d}x\) | |
| \(V=\displaystyle\int\limits_{0}^{2}\left(x^2+3\right)\mathrm{\,d}x\) |
Cho hàm số \(y=\pi^x\) có đồ thị \((C)\). Gọi \(D\) là hình phẳng giới hạn bởi \((C)\), trục hoành và hai đường thẳng \(x=2\), \(x=3\). Thể tích của khối tròn xoay tạo thành khi quay \(D\) quanh trục hoành được tính bởi công thức
| \(V=\pi^2\displaystyle\int\limits_{2}^{3}\pi^x\mathrm{\,d}x\) | |
| \(V=\pi^3\displaystyle\int\limits_{2}^{3}\pi^x\mathrm{\,d}x\) | |
| \(V=\pi\displaystyle\int\limits_{2}^{3}\pi^{2x}\mathrm{\,d}x\) | |
| \(V=\pi\displaystyle\int\limits_{3}^{2}\pi^{2x}\mathrm{\,d}x\) |
Thể tích khối tròn xoay tạo thành do hình phẳng giới hạn bởi các đường \(y=\dfrac{x}{4}\), \(y=0\), \(x=1\), \(x=4\) quay quanh trục \(Ox\) là
| \(\dfrac{21\pi}{16}\) | |
| \(\dfrac{15}{16}\) | |
| \(\dfrac{21}{16}\) | |
| \(\dfrac{15\pi}{8}\) |
Thể tích khối tròn xoay có được khi quay quanh trục \(Ox\) hình phẳng giới hạn bởi các đường \(y=\sqrt{x}\), \(y=0\), \(x=0\), \(x=1\) bằng
| \(V=\dfrac{\pi}{2}\) | |
| \(V=\dfrac{2\pi}{3}\) | |
| \(V=\dfrac{2}{3}\) | |
| \(V=\dfrac{1}{2}\) |
Cho hình phẳng \((H)\) giới hạn bởi đồ thị hàm số \(y=-x^2+3x-2\), trục hoành và hai đường thẳng \(x=1\), \(x=2\). Quay \((H)\) xung quanh trục hoành được khối tròn xoay có thể tích là
| \(V=\displaystyle\int\limits_{1}^{2}\left|x^2-3x+2\right|\mathrm{\,d}x\) | |
| \(V=\displaystyle\int\limits_{1}^{2}\left|x^2-3x+2\right|^2\mathrm{\,d}x\) | |
| \(V=\pi\displaystyle\int\limits_{1}^{2}\left(x^2-3x+2\right)^2\mathrm{\,d}x\) | |
| \(V=\pi\displaystyle\int\limits_{1}^{2}\left|x^2-3x+2\right|\mathrm{\,d}x\) |
