Hình vẽ sau đây là đồ thị của hàm số nào?

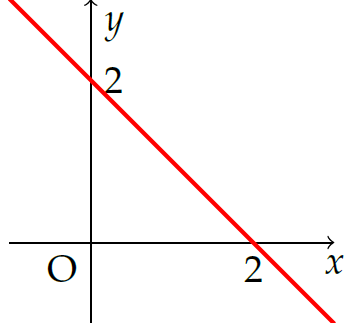
	\(y=2-x\)
	\(y=x-2\)
	\(y=2-2x\)
	\(y=1-2x\)

Hình vẽ nào dưới đây là đồ thị của hàm số \(y=\dfrac{x}{2}-2\)?

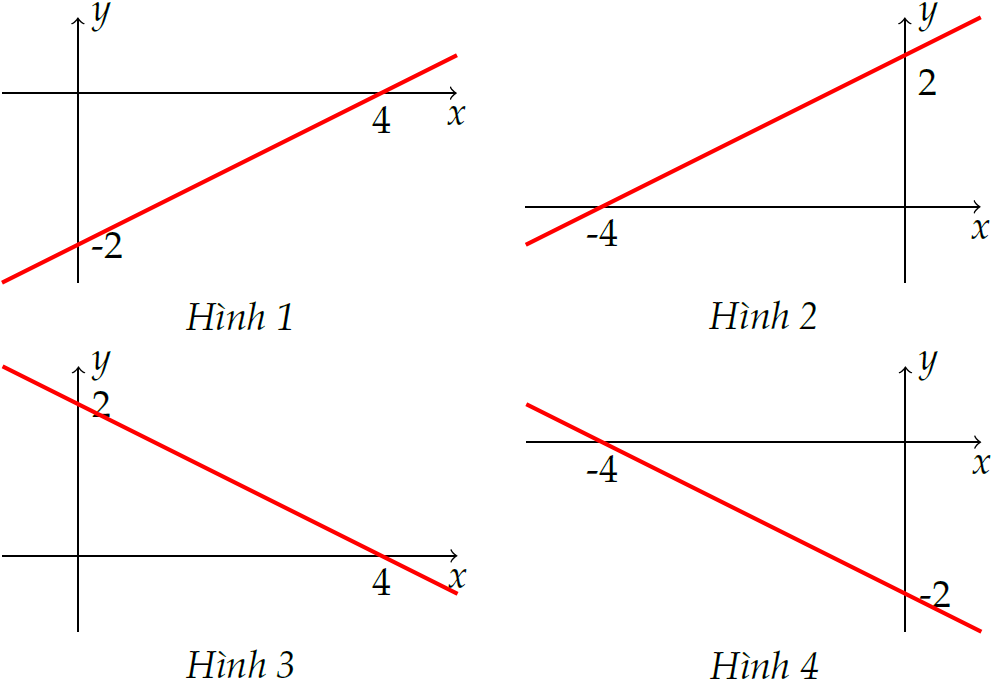
	Hình 1
	Hình 2
	Hình 3
	Hình 4

Đường thẳng \(\Delta\) đi qua điểm \(M(6;13)\) và vuông góc với đường thẳng \(d\colon y=3x-2019\) có phương trình là

	\(y=3x-5\)
	\(y=\dfrac{x}{3}+11\)
	\(y=-\dfrac{x}{3}-2019\)
	\(y=-\dfrac{x}{3}+15\)

Tìm điều kiện của tham số \(m\) để hàm số \(y=(m-3)x+2019\) luôn nghịch biến trên \(\Bbb{R}\).

	\(m>3\)
	\(m\leq3\)
	\(m<3\)
	\(m\neq3\)

Hàm số nào dưới đây là hàm số chẵn?

	\(y=\sqrt{x-3}\)
	\(y=-x^4+3x^2-2019\)
	\(y=(x-3)^2\)
	\(y=2x^3-2019x\)

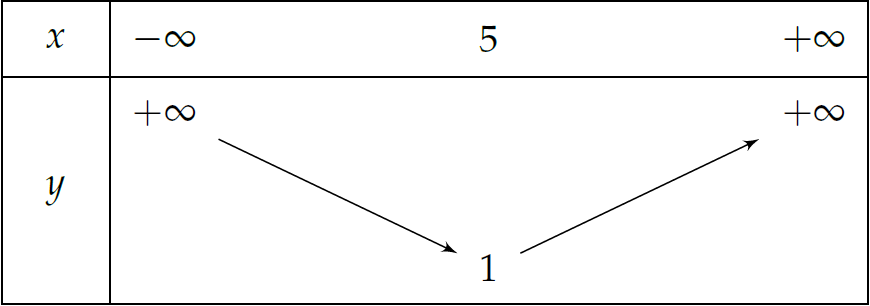
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình vẽ. Tìm khoảng đồng biến của hàm số.

	\((-\infty;5)\)
	\((-\infty;1)\)
	\((1;+\infty)\)
	\((5;+\infty)\)

Tìm tập xác định của hàm số $$f(x)=\dfrac{x+7}{\sqrt{x-7}}$$

	\(\mathscr{D}=(7;+\infty)\)
	\(\mathscr{D}=[7;+\infty)\)
	\(\mathscr{D}=\Bbb{R}\setminus\{7\}\)
	\(\mathscr{D}=(-\infty;7)\)

Tìm tập xác định của hàm số $$f(x)=\dfrac{x+7}{x-7}$$

	\(\mathscr{D}=\Bbb{R}\setminus\{-7\}\)
	\(\mathscr{D}=\Bbb{R}\setminus\{\pm7\}\)
	\(\mathscr{D}=\Bbb{R}\)
	\(\mathscr{D}=\Bbb{R}\setminus\{7\}\)

Điểm nào dưới đây thuộc đồ thị của hàm số \(f(x)=\sqrt{x-3}\)?

	\(A(5;2)\)
	\(B(0;-3)\)
	\(C(2;-1)\)
	\(D(3;0)\)

Cho hai tập hợp \(A=(-\infty;2020]\) và \(B=(2019;+\infty)\). Xác định tập hợp \(A\cup B\).

	\((2019;2020)\)
	\(\varnothing\)
	\((2019;2020]\)
	\(\Bbb{R}\)

Cho hai tập hợp \(A=(-\infty;2020]\) và \(B=(2019;+\infty)\). Xác định tập hợp \(A\cap B\).

	\((2019;2020)\)
	\(\varnothing\)
	\((2019;2020]\)
	\(\Bbb{R}\)

Cho hai tập hợp \(A=\{1;3;5;7;9\}\) và \(B=\{2;3;5;7\}\). Xác định tập hợp \(A\setminus B\).

	\(\{3;5;7\}\)
	\(\{1;2;3;5;7;9\}\)
	\(\{2\}\)
	\(\{1;9\}\)

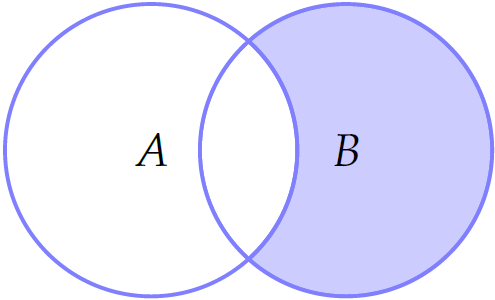
Cho hai tập hợp \(A,\,B\) được minh họa bằng biểu đồ Ven như hình vẽ. Phần được tô màu là tập hợp nào sau đây?

	\(A\setminus B\)
	\(A\cap B\)
	\(A\cup B\)
	\(B\setminus A\)

Tập hợp \(B=\{a;b;c;d;e;f\}\) có bao nhiêu tập con?

	\(36\)
	\(7\)
	\(32\)
	\(64\)

Liệt kê các phần tử của tập hợp $$A=\left\{n(n+1)\,|\,n\in\Bbb{N},\,-3<n\leq3\right\}$$

	\(A=\varnothing\)
	\(A=\{-2;-1;0;1;2;3\}\)
	\(A=\{0;2;6;12\}\)
	\(A=\{0;2;6\}\)

Tìm mệnh đề phủ định của mệnh đề $$''\exists x\in\Bbb{Z}\,\colon\,x^2=2''$$

	\(''\exists x\notin\Bbb{Z}\colon\,x^2\neq2''\)
	\(''\exists x\in\Bbb{N}\colon\,x^2\neq2''\)
	\(''\forall x\in\Bbb{Z}\colon\,x^2\neq2''\)
	\(''\forall x\notin\Bbb{Z}\colon\,x^2=2''\)

Trong các khẳng định sau, khẳng định nào là mệnh đề?

	\(x^2-4x+3=0\)
	\(n\) là số chẵn
	Quần đảo Trường Sa là của Việt Nam
	Đề thi khó hay dễ?

Tập nghiệm của bất phương trình \(\log_2^2x-3\log_2x+2<0\) là khoảng \((a;b)\). Tính \(a^2+b^2\).

	\(16\)
	\(5\)
	\(20\)
	\(10\)

Tìm số nghiệm nguyên của bất phương trình $$2\log_{\tfrac{1}{2}}|x-1|<\log_{\tfrac{1}{2}}x-1$$

	\(1\)
	\(3\)
	\(2\)
	Vô số

Có bao nhiêu số nguyên \(x\) thỏa mãn bất phương trình \(\log_{\tfrac{1}{2}}\left[\log_2\left(2-x^2\right)\right]>0\)?

	Vô số
	\(1\)
	\(0\)
	\(2\)