Trong không gian \(Oxyz\), cho điểm \(M(1;0;4)\) và đường thẳng \(d\colon\dfrac{x}{1}=\dfrac{y-1}{-1}=\dfrac{x+1}{2}\). Tìm hình chiếu vuông góc \(H\) của \(M\) lên đường thẳng \(d\).

	\(H(2;-1;3)\)
	\(H(1;0;1)\)
	\(H(-2;3;0)\)
	\(H(0;1;-1)\)

Trong không gian \(Oxyz\), cho \(d\) là đường thẳng đi qua \(A(1;2;3)\) và vuông góc với mặt phẳng \((\alpha)\colon4x+3y-7z+1=0\). Phương trình tham số của đường thẳng \(d\) là

	\(\begin{cases}x=1+3t\\ y=2-4t\\ z=3-7t\end{cases}\)
	\(\begin{cases}x=1+4t\\ y=2+3t\\ z=3-7t\end{cases}\)
	\(\begin{cases}x=-1+8t\\ y=-2+6t\\ z=-3-14t\end{cases}\)
	\(\begin{cases}x=-1+4t\\ y=-2+3t\\ z=-3-7t\end{cases}\)

Trong không gian \(Oxyz\), phương trình đường thẳng đi qua \(A(1;-2;3)\) và có vectơ chỉ phương \(\overrightarrow{u}=(2;-1;-2)\) là

	\(\dfrac{x+1}{2}=\dfrac{y-2}{-1}=\dfrac{z+3}{-2}\)
	\(\dfrac{x-1}{-2}=\dfrac{y+2}{-1}=\dfrac{z-3}{2}\)
	\(\dfrac{x-1}{4}=\dfrac{y+2}{-2}=\dfrac{z-3}{-4}\)
	\(\dfrac{x-1}{-2}=\dfrac{y+2}{1}=\dfrac{z-3}{-2}\)

Trong không gian \(Oxyz\), điểm nào dưới đây thuộc đường thẳng \(d\colon\dfrac{x+2}{1}=\dfrac{y-1}{1}=\dfrac{z+2}{2}\)?

	\(Q(-2;1;-2)\)
	\(M(-2;-2;1)\)
	\(N(2;-1;2)\)
	\(P(1;1;2)\)

Trong không gian \(Oxyz\), mặt phẳng \((P)\colon x+\sqrt{2}y-z+3=0\) cắt mặt cầu \((S)\colon x^2+y^2+z^2=5\) theo giao tuyến là đường tròn có diện tích là

	\(\dfrac{7\pi}{4}\)
	\(\dfrac{15\pi}{4}\)
	\(\dfrac{9\pi}{4}\)
	\(\dfrac{11\pi}{4}\)

Trong không gian \(Oxyz\), cho \(A(2;-3;0)\) và mặt phẳng \((\alpha)\colon x+2y-z+3=0\). Tìm phương trình mặt phẳng \((P)\) đi qua \(A\) sao cho \((P)\) vuông góc với \((\alpha)\) và \((P)\) song song với trục \(Oz\)?

	\(2x+y-1=0\)
	\(y+2z+3=0\)
	\(2x-y-7=0\)
	\(x+2y-z+4=0\)

Trong không gian \(Oxyz\), mặt phẳng đi qua điểm \(A(2;-1;2)\) và song song với mặt phẳng \((P)\colon2x-y+3z+2=0\) có phương trình là

	\(2x-y+3z+11=0\)
	\(2x-y-3z+11=0\)
	\(2x-y+3z-11=0\)
	\(2x-y+3z-9=0\)

Trong không gian \(Oxyz\), mặt cầu \((S)\colon x^2+y^2+z^2+4x-2y+2z-3=0\) có tâm và bán kính là

	\(I(2;-1;1),\,R=9\)
	\(I(2;-1;1),\,R=3\)
	\(I(-2;1;-1),\,R=3\)
	\(I(-2;1;-1),\,R=9\)

Trong không gian \(Oxyz\), cho ba điểm \(A(-1;-2;3)\), \(B(0;3;1)\), \(C(4;2;2)\). Côsin của góc \(\widehat{BAC}\) bằng

	\(-\dfrac{9}{\sqrt{35}}\)
	\(-\dfrac{9}{2\sqrt{35}}\)
	\(\dfrac{9}{\sqrt{35}}\)
	\(\dfrac{9}{2\sqrt{35}}\)

Trong không gian \(Oxyz\) cho ba điểm \(A(2;-1;5)\), \(B(5;-5;7)\), \(M(x;y;1)\). Với giá trị nào của \(x,\,y\) thì \(A,\,B,\,M\) thẳng hàng?

	\(x=4;\,y=7\)
	\(x=4;\,y=-7\)
	\(x=-4;\,y=7\)
	\(x=-4;\,y=-7\)

Trong không gian \(Oxyz\), cho hai vectơ \(\overrightarrow{u}=(1;2;3)\) và \(\overrightarrow{v}=(-5;1;1)\). Khẳng định nào đúng?

	\(\left|\overrightarrow{u}\right|=\left|\overrightarrow{v}\right|\)
	\(\overrightarrow{u}=\overrightarrow{v}\)
	\(\overrightarrow{u}\bot\overrightarrow{v}\)
	\(\overrightarrow{u}\) cùng phương với \(\overrightarrow{v}\)

Cho số phức \(z\) thỏa mãn \(\dfrac{\overline{z}+i}{z-1}=2-i\). Tìm số phức \(w=1+z+z^2\).

	\(w=5-2i\)
	\(5+2i\)
	\(w=\dfrac{9}{2}+2i\)
	\(w=\dfrac{9}{2}-2i\)

Cho số phức \(z=1+i\). Số phức nghịch đảo của \(z\) là

	\(1-i\)
	\(\dfrac{1-i}{2}\)
	\(\dfrac{1-i}{\sqrt{2}}\)
	\(\dfrac{-1+i}{2}\)

Tìm phần thực, phần ảo của số phức $$z=\dfrac{3-i}{1+i}+\dfrac{2+i}{i}.$$

	Phần thực là \(2\), phần ảo là \(4i\)
	Phần thực là \(2\), phần ảo là \(-4i\)
	Phần thực là \(2\), phần ảo là \(4\)
	Phần thực là \(2\), phần ảo là \(-4\)

Cho hai số phức \(z_1,\,z_2\) thỏa mãn \(\left|z_1\right|=2\), \(\left|z_2\right|=\sqrt{3}\). Gọi \(M,\,N\) là các điểm biểu diễn cho \(z_1\) và \(iz_2\). Biết \(\widehat{MON}=30^\circ\). Tính \(S=\left|z_1^2+4z_2^2\right|\).

	\(4\sqrt{7}\)
	\(3\sqrt{3}\)
	\(5\sqrt{2}\)
	\(\sqrt{5}\)

Cho hai số phức \(z_1=2+3i\), \(z_2=4+5i\). Số phức liên hợp của số phức \(w=2\left(z_1+z_2\right)\) là

	\(\overline{w}=28i\)
	\(\overline{w}=12+8i\)
	\(\overline{w}=8+10i\)
	\(\overline{w}=12-16i\)

Cho hai số phức \(z_1=2-2i\), \(z_2=-3+3i\). Khi đó số phức \(z_1-z_2\) là

	\(-1+i\)
	\(-5+5i\)
	\(5-5i\)
	\(-5i\)

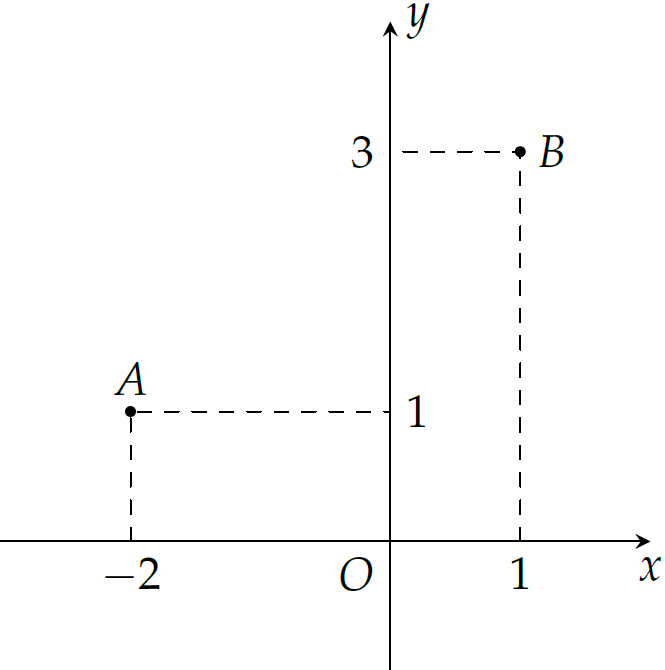
Trong mặt phẳng \(Oxy\), cho các điểm \(A,\,B\) như hình vẽ trên. Trung điểm của đoạn thẳng \(AB\) biểu diễn số phức

	\(-\dfrac{1}{2}+2i\)
	\(2-\dfrac{1}{2}i\)
	\(-1+2i\)
	\(2-i\)

Số phức \(-3+7i\) có phần ảo bằng

	\(-7\)
	\(-3\)
	\(3\)
	\(7\)

Kí hiệu \((H)\) là hình phẳng giới hạn bởi đồ thị \(y=x^2-ax\) với trục hoành (\(a\neq0\)). Quay hình \((H)\) xung quanh trục hoành ta thu được khối tròn xoay có thể tích \(V=\dfrac{16\pi}{15}\). Tìm \(a\).

	\(a=-2\)
	\(a=-3\)
	\(a=\pm2\)
	\(a=2\)