Tập hợp các số phức $z$ thỏa mãn $|z+1-2i|=3$ là đường tròn có tâm
| $I(-1;2)$ | |
| $I(-1;-2)$ | |
| $I(1;-2)$ | |
| $I(1;2)$ |
Tính thể tích của vật thể tròn xoay được sinh ra khi hình $(H)$ quay quanh trục $Ox$ với $(H)$ được giới hạn bởi đồ thị hàm số $y=\sqrt{4x-x^2}$ và trục hoành.
| $\dfrac{34\pi}{3}$ | |
| $\dfrac{35\pi}{3}$ | |
| $\dfrac{32\pi}{3}$ | |
| $\dfrac{31\pi}{3}$ |
Trong không gian $Oxyz$, cho điểm $M(3;2;-1)$ và mặt phẳng $(P)\colon x+z-2=0$. Đường thẳng đi qua $M$ và vuông góc với $(P)$ có phương trình là
| $\begin{cases}x=3+t\\ y=2\\ z=-1+t\end{cases}$ | |
| $\begin{cases}x=3+t\\ y=2t\\ z=1-t\end{cases}$ | |
| $\begin{cases}x=3+t\\ y=1+2t\\ z=-t\end{cases}$ | |
| $\begin{cases}x=3+t\\ y=2+t\\ z=-1\end{cases}$ |
Trong không gian $Oxyz$, viết phương trình đường thẳng đi qua hai điểm $P(1;1;-1)$, $Q(2;3;2)$.
| $\dfrac{x-1}{2}=\dfrac{y-1}{3}=\dfrac{z+1}{2}$ | |
| $\dfrac{x+1}{1}=\dfrac{y+3}{2}=\dfrac{z+2}{3}$ | |
| $\dfrac{x-1}{1}=\dfrac{y-1}{2}=\dfrac{z+1}{3}$ | |
| $\dfrac{x-1}{1}=\dfrac{y-2}{1}=\dfrac{z-3}{-1}$ |
Tính $\displaystyle\displaystyle\int x\ln x\mathrm{\,d}x$.
| $\dfrac{1}{2}x^2\ln x-\dfrac{1}{2}x+C$ | |
| $\dfrac{1}{2}\ln x^2-\dfrac{1}{4}x^2+C$ | |
| $\dfrac{1}{2}x^2\ln x-\dfrac{1}{2}x^2+C$ | |
| $\dfrac{1}{2}x^2\ln x-\dfrac{1}{4}x^2+C$ |
Cho số phức $z=1-3i$. Số phức $w=(1-i)z+\overline{z}$ có phần ảo bằng
| $1$ | |
| $-1$ | |
| $-i$ | |
| $i$ |
Cho số phức $z=a+bi$ ($a,\,b\in\mathbb{R}$) tùy ý. Mệnh đề nào sau đây đúng?
| Số phức liên hợp của $z$ có mô-đun bằng mô-đun của $iz$ | |
| $z^2=|z|^2$ | |
| Điểm $M(-a;b)$ là điểm biểu diễn của $\overline{z}$ | |
| Mô-đun của $z$ là một số thực dương |
Cho số phức $z$ thỏa mãn $z=\dfrac{\left(1+\sqrt{3}i\right)^3}{1-i}$. Tìm mô-đun của $iz$.
| $4$ | |
| $4\sqrt{2}$ | |
| $8\sqrt{2}$ | |
| $8$ |
Tính $\displaystyle\displaystyle\int\limits_{0}^{\tfrac{1}{2}}\dfrac{2x-1}{x+1}\mathrm{\,d}x$.
| $1-3\ln3+3\ln2$ | |
| $-1-3\ln3+3\ln2$ | |
| $2-3\ln3+3\ln2$ | |
| $1+3\ln3-3\ln2$ |
Tìm nguyên hàm của hàm số $f(x)=\cos\left(3x+\dfrac{\pi}{6}\right)$.
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=-\dfrac{1}{3}\sin\left(3x+\dfrac{\pi}{6}\right)+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=\sin\left(3x+\dfrac{\pi}{6}\right)+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=\dfrac{1}{3}\sin\left(3x+\dfrac{\pi}{6}\right)+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=\dfrac{1}{6}\sin\left(3x+\dfrac{\pi}{6}\right)+C$ |
Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$. Gọi $S$ là diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=f(x)$, trục hoành, đường thẳng $x=-1$, $x=5$ (như hình vẽ).
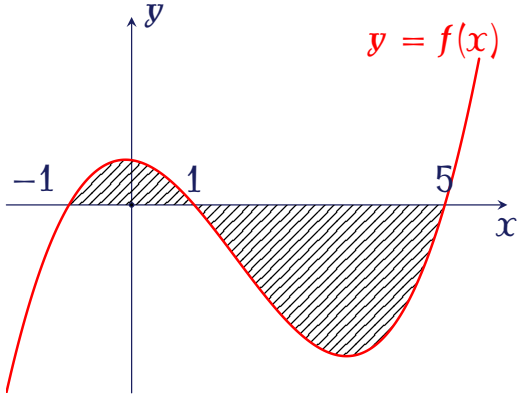
Mệnh đề nào sau đây đúng?
| $S=\displaystyle\displaystyle\int\limits_{-1}^{1}f(x)\mathrm{\,d}x+\displaystyle\int\limits_{1}^{5}f(x)\mathrm{\,d}x$ | |
| $S=-\displaystyle\displaystyle\int\limits_{-1}^{1}f(x)\mathrm{\,d}x-\displaystyle\int\limits_{1}^{5}f(x)\mathrm{\,d}x$ | |
| $S=\displaystyle\displaystyle\int\limits_{-1}^{1}f(x)\mathrm{\,d}x-\displaystyle\int\limits_{1}^{5}f(x)\mathrm{\,d}x$ | |
| $S=-\displaystyle\displaystyle\int\limits_{-1}^{1}f(x)\mathrm{\,d}x+\displaystyle\int\limits_{1}^{5}f(x)\mathrm{\,d}x$ |
Nếu $\displaystyle\displaystyle\int\limits_{1}^{2}f(x)\mathrm{\,d}x=-2$ và $\displaystyle\displaystyle\int\limits_{2}^{3}f(x)\mathrm{\,d}x=1$ thì $\displaystyle\displaystyle\int\limits_{1}^{3}f(x)\mathrm{\,d}x$ bằng
| $1$ | |
| $-3$ | |
| $-1$ | |
| $3$ |
Cho $f(x)$ là hàm số liên tục trên $[a;b]$ và $F(x)$ là một nguyên hàm của $f(x)$. Khẳng định nào sau đây đúng?
| $\displaystyle\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x=F(x)\bigg|_a^b=F(b)-F(a)$ | |
| $\displaystyle\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x=f(x)\bigg|_a^b=f(b)-f(a)$ | |
| $\displaystyle\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x=F(x)\bigg|_a^b=-F(b)-F(a)$ | |
| $\displaystyle\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x=F(x)\bigg|_a^b=F(a)-F(b)$ |
Cho hai hàm số $u=u(x)$, $v=v(x)$ có đạo hàm liên tục. Khi đó, $\displaystyle\displaystyle\int u\mathrm{d}v$ bằng
| $uv-\displaystyle\displaystyle\int v\mathrm{d}u$ | |
| $uv+\displaystyle\displaystyle\int v\mathrm{d}u$ | |
| $-uv-\displaystyle\displaystyle\int v\mathrm{d}u$ | |
| $-uv+\displaystyle\displaystyle\int v\mathrm{d}u$ |
Cho $z_1=5+3i$, $z_2=-8+9i$. Tọa độ điểm biểu diễn hình học của $z=z_1+z_2$ là
| $P(3;-12)$ | |
| $Q(3;12)$ | |
| $M(14;-5)$ | |
| $N(-3;12)$ |
Trong không gian $Oxyz$, cho vectơ $\overrightarrow{a}=-3\overrightarrow{j}+4\overrightarrow{k}$. Tọa độ của vectơ $\overrightarrow{a}$ là
| $(0;-4;3)$ | |
| $(-3;0;4)$ | |
| $(0;3;4)$ | |
| $(0;-3;4)$ |
Họ tất cả các nguyên hàm của hàm số $f(x)=\cos x+6x$ là
| $-\sin x+C$ | |
| $\sin x+6x^2+C$ | |
| $-\sin x+3x^2+C$ | |
| $\sin x+3x^2+C$ |
Cho hàm số $f(x)$ và $g(x)$ cùng liên tục trên $\mathbb{R}$. Khẳng định nào đúng?
| $\displaystyle\displaystyle\int\big[f(x)\cdot g(x)\big]\mathrm{\,d}x=\left(\displaystyle\int f(x)\mathrm{\,d}x\right)\cdot\left(\displaystyle\int g(x)\mathrm{\,d}x\right)$ | |
| $\displaystyle\displaystyle\int\big(f(x)-g(x)\big)\mathrm{\,d}x=\displaystyle\int g(x)\mathrm{\,d}x-\displaystyle\int f(x)\mathrm{\,d}x$ | |
| $\displaystyle\displaystyle\int\big[f(x)+g(x)\big]\mathrm{\,d}x=\displaystyle\int f(x)\mathrm{\,d}x+\displaystyle\int g(x)\mathrm{\,d}x$ | |
| $\displaystyle\displaystyle\int\left[\dfrac{f(x)}{g(x)}\right]\mathrm{\,d}x=\dfrac{\displaystyle\int f(x)\mathrm{\,d}x}{\displaystyle\int g(x)\mathrm{\,d}x}$ |
Trong không gian $Oxyz$, cho đường thẳng $(d)\colon\begin{cases} x=1-t\\ y=-2+2t\\ z=1+t \end{cases}$. Vectơ nào là vectơ chỉ phương của $d$?
| $\overrightarrow{u}=(-1;-2;1)$ | |
| $\overrightarrow{u}=(1;2;1)$ | |
| $\overrightarrow{u}=(1;-2;1)$ | |
| $\overrightarrow{u}=(-1;2;1)$ |
Gọi $z_1,\,z_2$ là hai nghiệm của phương trình $z^2-6z+10=0$. Giá trị của $z_1^2+z_2^2$ bằng
| $56$ | |
| $26$ | |
| $20$ | |
| $16$ |
