Cho hai số phức \(z_1,\,z_2\) thỏa mãn \(\left|z_1\right|=2\), \(\left|z_2\right|=\sqrt{3}\). Gọi \(M,\,N\) là các điểm biểu diễn cho \(z_1\) và \(iz_2\). Biết \(\widehat{MON}=30^\circ\). Tính \(S=\left|z_1^2+4z_2^2\right|\).

	\(4\sqrt{7}\)
	\(3\sqrt{3}\)
	\(5\sqrt{2}\)
	\(\sqrt{5}\)

Cho hai số phức \(z_1=2+3i\), \(z_2=4+5i\). Số phức liên hợp của số phức \(w=2\left(z_1+z_2\right)\) là

	\(\overline{w}=28i\)
	\(\overline{w}=12+8i\)
	\(\overline{w}=8+10i\)
	\(\overline{w}=12-16i\)

Cho hai số phức \(z_1=2-2i\), \(z_2=-3+3i\). Khi đó số phức \(z_1-z_2\) là

	\(-1+i\)
	\(-5+5i\)
	\(5-5i\)
	\(-5i\)

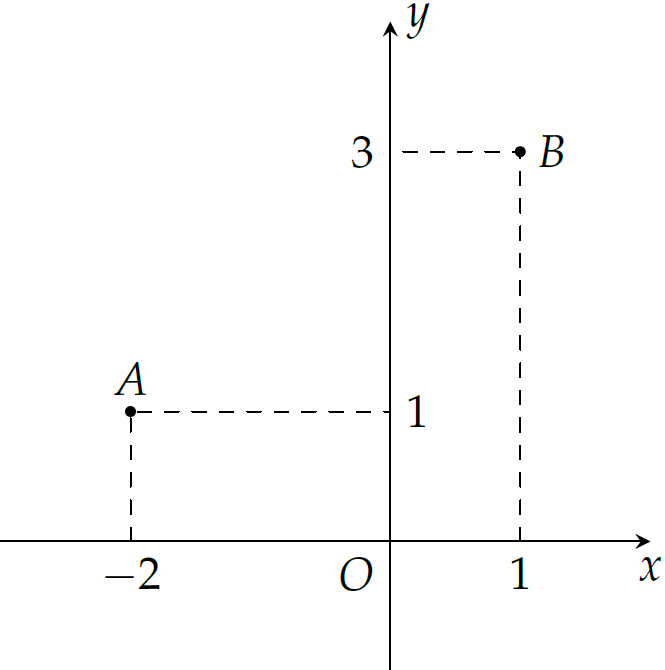
Trong mặt phẳng \(Oxy\), cho các điểm \(A,\,B\) như hình vẽ trên. Trung điểm của đoạn thẳng \(AB\) biểu diễn số phức

	\(-\dfrac{1}{2}+2i\)
	\(2-\dfrac{1}{2}i\)
	\(-1+2i\)
	\(2-i\)

Số phức \(-3+7i\) có phần ảo bằng

	\(-7\)
	\(-3\)
	\(3\)
	\(7\)

Kí hiệu \((H)\) là hình phẳng giới hạn bởi đồ thị \(y=x^2-ax\) với trục hoành (\(a\neq0\)). Quay hình \((H)\) xung quanh trục hoành ta thu được khối tròn xoay có thể tích \(V=\dfrac{16\pi}{15}\). Tìm \(a\).

	\(a=-2\)
	\(a=-3\)
	\(a=\pm2\)
	\(a=2\)

Cho hình phẳng \((D)\) giới hạn bởi đồ thị hàm số \(y=\sqrt{x}\), hai đường thẳng \(x=1\), \(x=2\) và trục hoành. Tính thể tích khối tròn xoay tạo thành khi quay \((D)\) quanh trục hoành.

	\(3\pi\)
	\(\dfrac{3}{2}\)
	\(\dfrac{3\pi}{2}\)
	\(\dfrac{2\pi}{3}\)

Cho hình \(D\) giới hạn bởi các đường \(y=x^2-2\) và \(y=-|x|\). Khi đó diện tích của hình \(D\) là

	\(\dfrac{13}{3}\)
	\(\dfrac{7\pi}{3}\)
	\(\dfrac{7}{3}\)
	\(\dfrac{13\pi}{3}\)

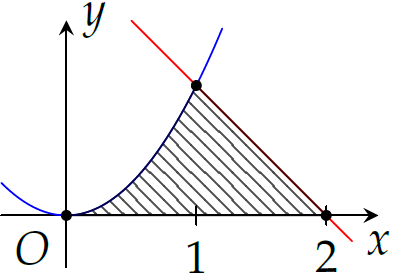
Tính diện tích hình phẳng tạo thành bởi parabol \(y=x^2\), đường thẳng \(y=-x+2\) và trục hoành trên đoạn \([0;2]\) (phần gạch sọc trong hình vẽ).

	\(\dfrac{5}{6}\)
	\(\dfrac{7}{6}\)
	\(\dfrac{2}{3}\)
	\(\dfrac{3}{5}\)

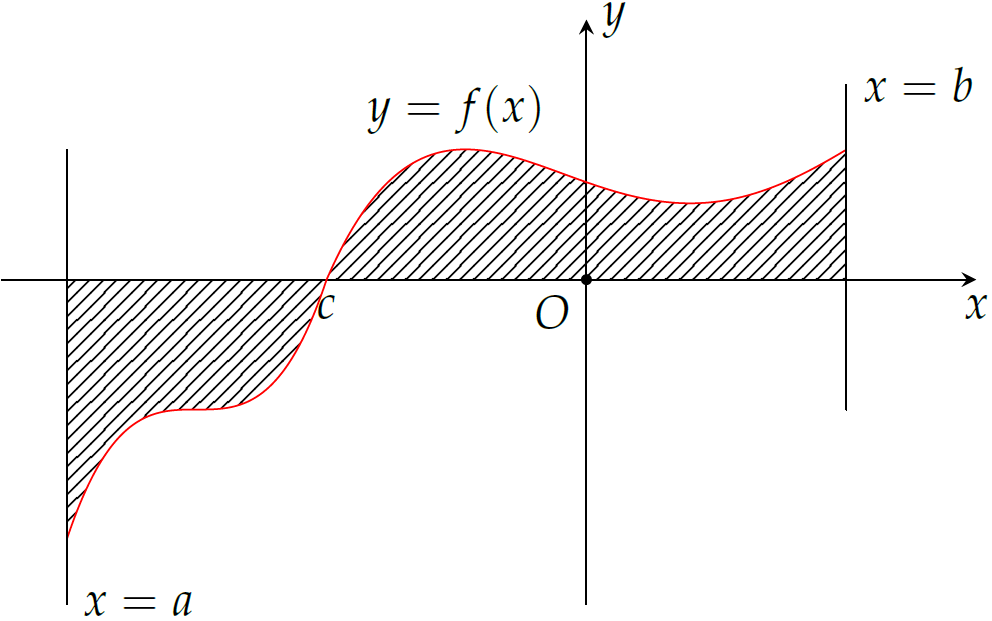
Diện tích hình phẳng \((H)\) giới hạn bởi đồ thị của hàm số \(y=f(x)\), trục hoành và hai đường thẳng \(x=a\), \(x=b\) (\(a<b\) và \(f(x)\) liên tục trên \([a;b]\)) (phần gạch sọc trong hình vẽ) tính theo công thức

	\(S=-\displaystyle\int\limits_{a}^{c}f(x)\mathrm{\,d}x+\displaystyle\int\limits_{c}^{b}f(x)\mathrm{\,d}x\)
	\(S=\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x\)
	\(S=\left|\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x\right|\)
	\(S=\displaystyle\int\limits_{a}^{c}f(x)\mathrm{\,d}x+\displaystyle\int\limits_{c}^{b}f(x)\mathrm{\,d}x\)

Nếu hàm số \(y=f(x)\) liên tục trên đoạn \([a;b]\) thì diện tích \(S\) của hình phẳng giới hạn bởi đồ thị hàm số \(y=f(x)\), trục hoành và hai đường thẳng \(x=a\), \(x=b\) là

	\(\displaystyle\int\limits_{a}^{b}\left|f(x)-g(x)\right|\mathrm{\,d}x\)
	\(\displaystyle\int\limits_{b}^{a}\left|f(x)\right|\mathrm{\,d}x\)
	\(\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x\)
	\(\displaystyle\int\limits_{a}^{b}\left|f(x)\right|\mathrm{\,d}x\)

Hàm số \(y=f(x)\) liên tục trên \([1;4]\) và thỏa mãn \(f(x)=\dfrac{f\left(2\sqrt{x}-1\right)}{\sqrt{x}}+\dfrac{\ln x}{x}\). Tính tích phân \(I=\displaystyle\int\limits_{3}^{4}f(x)\mathrm{\,d}x\).

	\(I=3+2\ln^22\)
	\(I=\ln^2\)
	\(I=2\ln2\)
	\(I=2\ln^22\)

Cho hàm số \(y=f(x)\) liên tục, nhận giá trị dương trên \((0;+\infty)\) và thỏa mãn \(f(1)=1\), \(f(x)=f'(x)\sqrt{3x+1}\), với mọi \(x>0\). Mệnh đề nào sau đây đúng?

	\(4< f(5)<5\)
	\(3< f(5)<4\)
	\(1< f(5)<2\)
	\(2< f(5)<3\)

Cho \(\displaystyle\int\limits_{0}^{1}\dfrac{x^2+1}{x+1}\mathrm{\,d}x=a+b\ln c\), với \(a\in\mathbb{Q}\), \(b\in\mathbb{Z}\), \(c\) là số nguyên tố. Ta có \(2a+b+c\) bằng

	\(5\)
	\(4\)
	\(3\)
	\(2\)

Giả sử tích phân \(I=\displaystyle\int\limits_{1}^{6}\dfrac{1}{2x+1}\mathrm{\,d}x=\ln M\), tìm \(M\).

	\(M=13\)
	\(M=4,33\)
	\(M=\sqrt{\dfrac{13}{3}}\)
	\(M=\dfrac{13}{3}\)

Cho hàm số \(y=f(x)\) có đạo hàm \(f'(x)\) liên tục trên \([0;2]\) và \(f(2)=3\), \(\displaystyle\int\limits_{0}^{2}f(x)\mathrm{\,d}x=3\). Tính \(\displaystyle\int\limits_{0}^{2}x\cdot f'(x)\mathrm{\,d}x\).

	\(6\)
	\(3\)
	\(0\)
	\(-3\)

Giá trị của tích phân \(\displaystyle\int\limits_{0}^{\tfrac{\pi}{4}}x\sin x\mathrm{\,d}x\) bằng

	\(\dfrac{4+\pi}{4\sqrt{2}}\)
	\(\dfrac{4-\pi}{4\sqrt{2}}\)
	\(\dfrac{2-\pi}{2\sqrt{2}}\)
	\(\dfrac{2+\pi}{2\sqrt{2}}\)

Cho hàm số \(y=f(x)\) có đạo hàm \(f'(x)=\dfrac{1}{2x-1}\) và \(f(1)=1\). Giá trị \(f(5)\) bằng

	\(1+\ln2\)
	\(1+\ln3\)
	\(\ln2\)
	\(\ln3\)

Cho hàm số \(f(x)\) có đạo hàm \(f'(x)\) liên tục trên \([a;b]\), \(f(b)=5\), \(\displaystyle\int\limits_{a}^{b}f'(x)\mathrm{\,d}x=3\sqrt{5}\). Tính \(f(a)\).

	\(f(a)=3\sqrt{5}\)
	\(f(a)=\sqrt{5}\left(\sqrt{5}-3\right)\)
	\(f(a)=\sqrt{3}\left(\sqrt{5}-3\right)\)
	\(f(a)=\sqrt{5}\left(3-\sqrt{5}\right)\)

Cho hàm số \(f(x),\,g(x)\) liên tục trên \([a;b]\). Khẳng định nào sau đây sai?

	\(\displaystyle\int\limits_{a}^{b}\left[f(x)+g(x)\right]\mathrm{\,d}x=\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x+\displaystyle\int\limits_{a}^{b}g(x)\mathrm{\,d}x\)
	\(\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x=\displaystyle\int\limits_{b}^{a}f(x)\mathrm{\,d}x\)
	\(\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x=\displaystyle\int\limits_{a}^{b}f(t)\mathrm{\,d}t\)
	\(\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x=\displaystyle\int\limits_{c}^{b}f(x)\mathrm{\,d}x+\displaystyle\int\limits_{a}^{c}f(x)\mathrm{\,d}x\)