Cho bảng biến thiên của hàm số \(y=f(x)\) như hình.

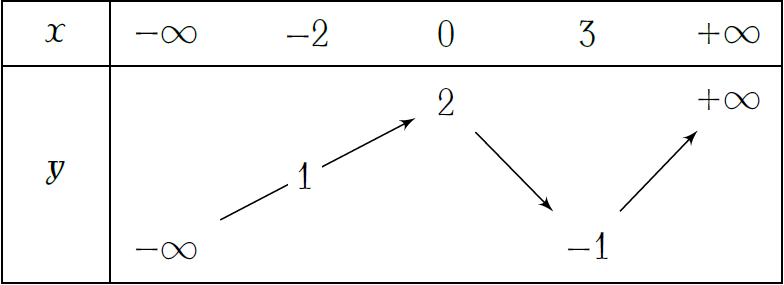
Tìm giá trị lớn nhất \(M\) và giá trị nhỏ nhất \(m\) của hàm số trên đoạn \([-2;3]\).

	\(\begin{cases}M=3\\ m=-2\end{cases}\)
	\(\begin{cases}M=0\\ m=3\end{cases}\)
	\(\begin{cases}M=2\\ m=-1\end{cases}\)
	\(\begin{cases}M=1\\ m=-1\end{cases}\)

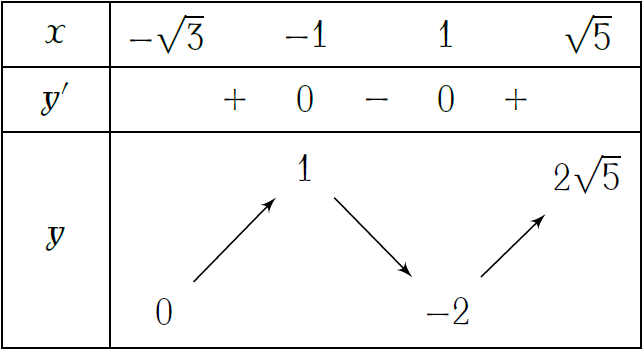
Cho hàm số \(y=f(x)\) xác định trên đoạn \(\left[-\sqrt{3};\sqrt{5}\right]\) và có bảng biến thiên như hình vẽ. Khẳng định nào sau đây là đúng?

	\(\min\limits_{\left[-\sqrt{3};\sqrt{5}\right]}f(x)=0\)
	\(\max\limits_{\left[-\sqrt{3};\sqrt{5}\right]}f(x)=2\)
	\(\max\limits_{\left[-\sqrt{3};\sqrt{5}\right]}f(x)=2\sqrt{5}\)
	\(\min\limits_{\left[-\sqrt{3};\sqrt{5}\right]}f(x)=2\)

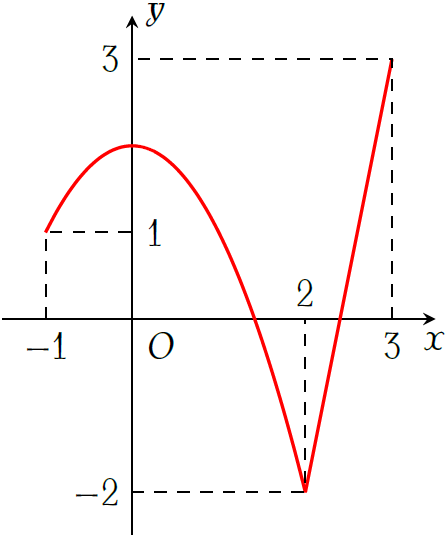
Cho hàm số \(y=f(x)\) liên tục trên đoạn \([-1;3]\) và có đồ thị như hình vẽ. Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn \([-1;3]\). Giá trị của \(M-m\) bằng

	\(0\)
	\(1\)
	\(4\)
	\(5\)

Đồ thị hàm số \(y=x^3-2mx^2+m^2x+n\) có tọa độ điểm cực tiểu là \((1;3)\). Khi đó \(m+n\) bằng

	\(4\)
	\(3\)
	\(2\)
	\(1\)

Với giá trị nào của tham số \(m\) thì hàm số \(y=x^3-mx^2+(2m-3)x-3\) đạt cực đại tại \(x=1\)?

	\(m\leq3\)
	\(m=3\)
	\(m<3\)
	\(m>3\)

Hàm số \(y=x^3-(m+2)x+m\) đạt cực tiểu tại \(x=1\) khi

	\(m=-1\)
	\(m=2\)
	\(m=-2\)
	\(m=1\)

Cho hàm số \(y=\dfrac{x^3}{3}-(m+1)x^2+mx-2\). Tìm \(m\) để hàm số đạt cực đại tại \(x=-1\).

	\(m=-1\)
	\(m=1\)
	Không có \(m\)
	\(m=-2\)

Cho hàm số \(y=x^3+3mx^2-2x+1\). Hàm số có điểm cực đại là \(x=-1\), khi đó giá trị của \(m\) thỏa mãn là

	\(m\in(-1;0)\)
	\(m\in(0;1)\)
	\(m\in(-3;-1)\)
	\(m\in(1;3)\)

Tập hợp các giá trị của tham số \(m\) để hàm số \(y=\dfrac{x^3}{3}-6x^2+(m-2)x+11\) có \(2\) điểm cực trị trái dấu.

	\((-\infty;38)\)
	\((-\infty;2)\)
	\((-\infty;2]\)
	\((2;38)\)

Tìm tất cả các giá trị của tham số \(m\) để hàm số \(y=x^3-3x^2+mx+1\) có \(2\) điểm cực trị.

	\(m\leq3\)
	\(m>3\)
	\(m>-3\)
	\(m<3\)

Tìm tất cả giá trị của tham số \(m\) để đồ thị hàm số \(y=x^4+(6m-4)x^2+1-m\) có \(3\) điểm cực trị.

	\(m\geq\dfrac{2}{3}\)
	\(m\leq\dfrac{2}{3}\)
	\(m>\dfrac{2}{3}\)
	\(m<\dfrac{2}{3}\)

Cho hàm số \(y=f(x)\) có bảng biến thiên như hình vẽ.

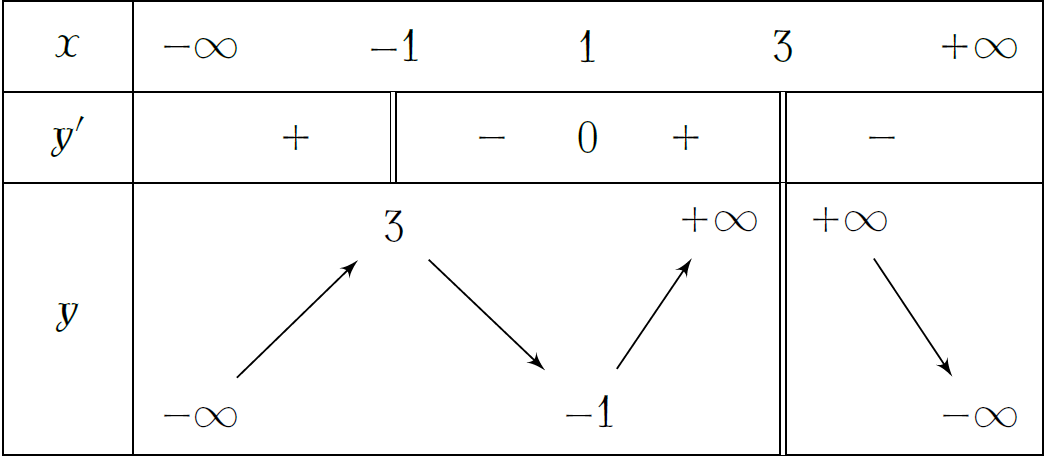
Số điểm cực trị của hàm số \(y=f(x)\) là

	\(0\)
	\(2\)
	\(3\)
	\(1\)

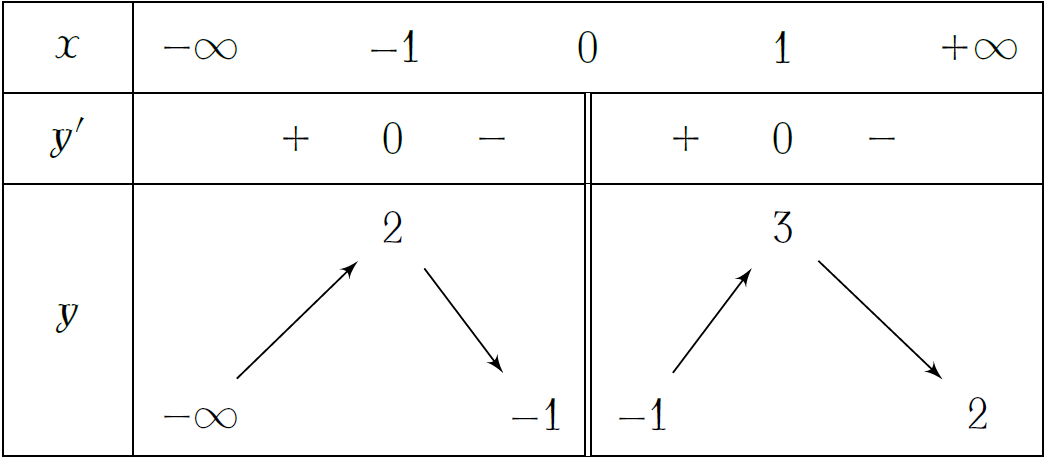
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình vẽ. Hỏi hàm số \(y=f(x)\) có bao nhiêu điểm cực trị?

	\(1\)
	\(3\)
	\(2\)
	\(4\)

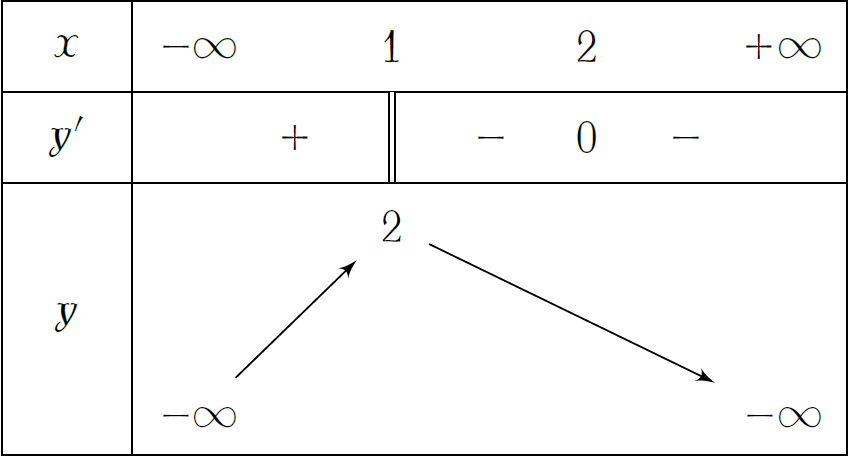
Cho hàm số \(y=f(x)\) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ. Khẳng định nào sau đây là đúng?

	Hàm số có giá trị cực đại bằng \(1\)
	Hàm số có đúng \(2\) cực trị
	Hàm số có giá trị cực đại bằng \(2\)
	Hàm số không xác định tại \(x=1\)

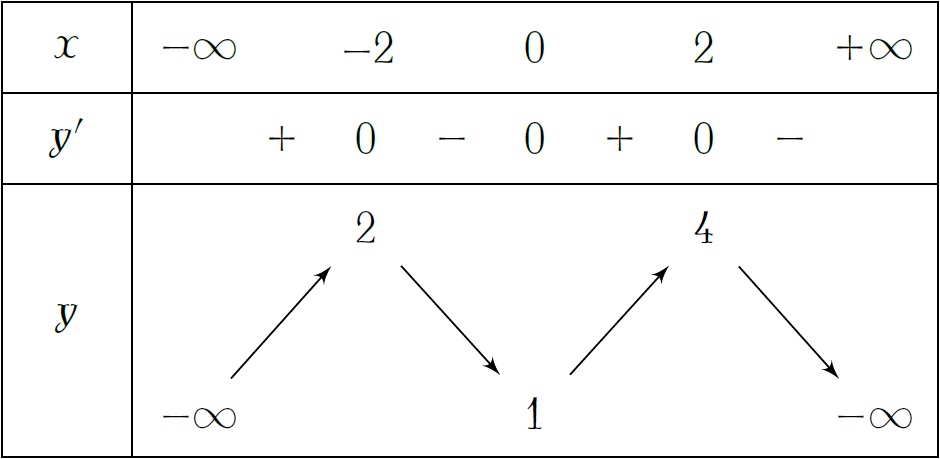
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình. Phát biểu nào sau đây đúng?

	Hàm số đạt cực đại tại \(x=2\)
	Hàm số đạt cực đại tại \(x=4\)
	Hàm số có \(3\) cực tiểu
	Hàm số có giá trị cực tiểu là \(0\)

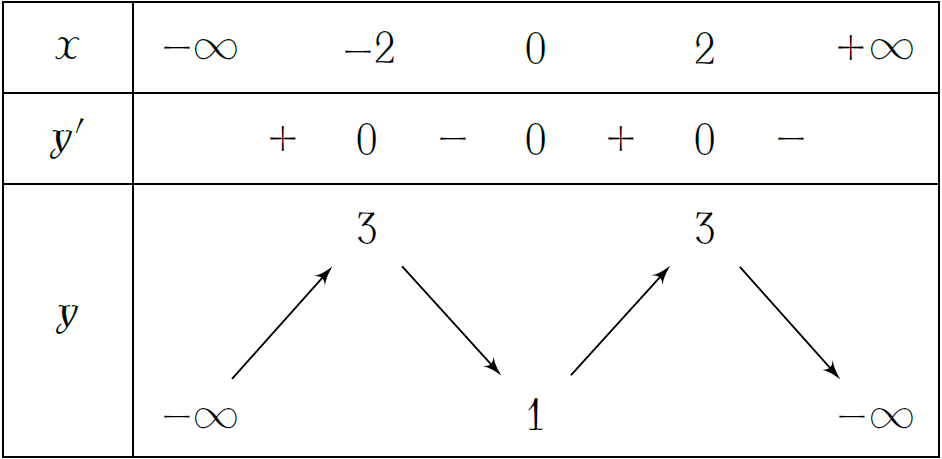
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình. Giá trị cực đại của hàm số bằng

	\(-2\)
	\(-1\)
	\(2\)
	\(3\)

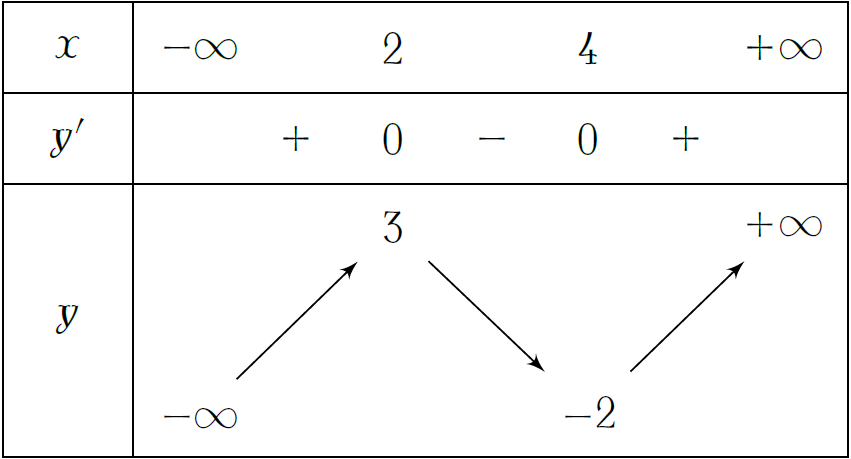
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình. Khẳng định nào sau đây là khẳng định đúng?

	Hàm số đạt cực đại tại \(x=2\)
	Hàm số đạt cực đại tại \(x=-2\)
	Hàm số đạt cực đại tại \(x=4\)
	Hàm số đạt cực đại tại \(x=3\)

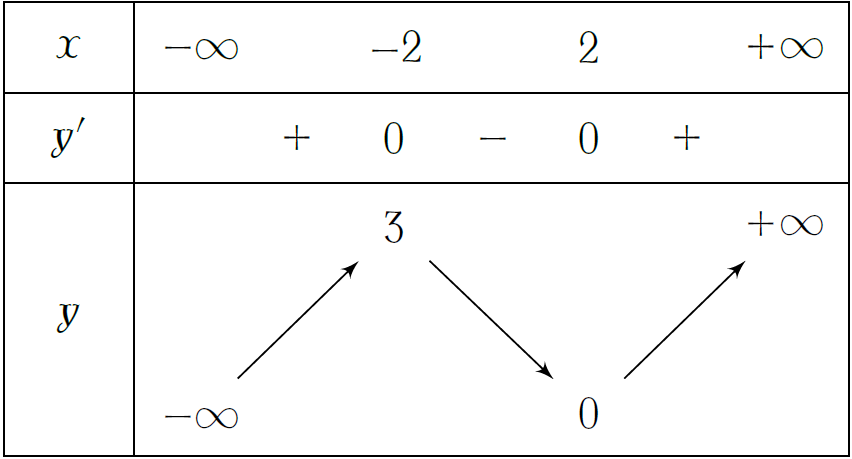
Cho hàm số \(y=f(x)\) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình. Tìm giá trị cực đại \(y_{\text{CĐ}}\) và giá trị cực tiểu \(y_{\text{CT}}\) của hàm số đã cho.

	\(y_{\text{CĐ}}=-2\) và \(y_{\text{CT}}=2\)
	\(y_{\text{CĐ}}=3\) và \(y_{\text{CT}}=0\)
	\(y_{\text{CĐ}}=2\) và \(y_{\text{CT}}=0\)
	\(y_{\text{CĐ}}=3\) và \(y_{\text{CT}}=-2\)

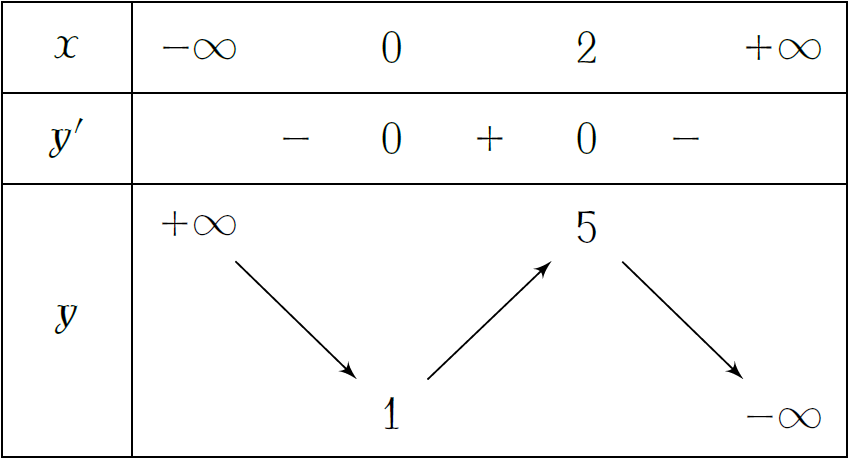
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình. Giá trị cực đại của hàm số bằng

	\(1\)
	\(2\)
	\(0\)
	\(5\)

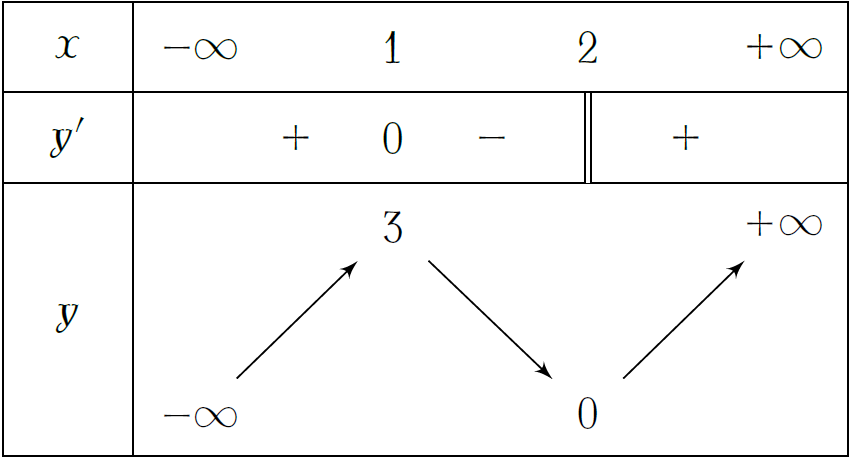
Hàm số \(y=f(x)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây là đúng?

	\(f(x)\) có \(2\) điểm cực trị
	\(f(x)\) có đúng \(1\) điểm cực trị
	\(f(x)\) không có giá trị cực tiểu
	\(f(x)\) không có giá trị cực đại