Tìm tiệm cận ngang của đồ thị hàm số \(f(x)=1+\dfrac{2x+2}{x-1}\).

	\(x=1\)
	\(y=1\)
	\(y=2\)
	\(y=3\)

Đường tiệm cận ngang của đồ thị hàm số \(y=\dfrac{2-2x}{x+1}\) là

	\(y=-2\)
	\(x=-1\)
	\(x=-2\)
	\(y=2\)

Đường tiệm cận ngang của đồ thị hàm số \(y=\dfrac{x-3}{x-1}\) là

	\(y=5\)
	\(y=0\)
	\(x=1\)
	\(y=1\)

Đường tiệm cận ngang của đồ thị hàm số \(y=\dfrac{2x-3}{x+4}\) là

	\(x=-4\)
	\(y=2\)
	\(x=4\)
	\(y=-\dfrac{3}{4}\)

Diện tích hình phẳng giới hạn bởi hai đường \(y=x^2-4\) và \(y=2x-4\) bằng

	\(36\)
	\(\dfrac{4}{3}\)
	\(\dfrac{4\pi}{3}\)
	\(36\pi\)

Biết \(F\left(x\right)=x^2\) là một nguyên hàm của hàm số \(f\left(x\right)\) trên \(\mathbb{R}\). Giá trị của \(\displaystyle\int\limits_1^2\left[2+f\left(x\right)\right]\mathrm{d}x\) bằng

	\(5\)
	\(3\)
	\(\dfrac{13}{3}\)
	\(\dfrac{7}{3}\)

Biết \(\displaystyle\int\limits_1^3f\left(x\right)\mathrm{d}x=3\). Giá trị của \(\displaystyle\int\limits_1^32f\left(x\right)\mathrm{d}x\) bằng

	\(5\)
	\(9\)
	\(6\)
	\(\dfrac{3}{2}\)

Cho hàm số \(f\left(x\right)=\dfrac{x}{\sqrt{x^2+2}}\). Họ tất cả các nguyên hàm của hàm số \(g\left(x\right)=\left(x+1\right)\cdot f'\left(x\right)\) là

	\(\dfrac{x^2+2x-2}{2\sqrt{x^2+2}}+C\)
	\(\dfrac{x-2}{\sqrt{x^2+2}}+C\)
	\(\dfrac{x^2+x+2}{\sqrt{x^2+2}}+C\)
	\(\dfrac{x+2}{2\sqrt{x^2+2}}+C\)

\(\displaystyle\int x^2\mathrm{\,d}x\) bằng

	\(2x+C\)
	\(\dfrac{1}{3}{x^3}+C\)
	\(x^3+C\)
	\(3x^3+C\)

Tập xác định của hàm số \(y=\log_5x\) là

	\(\left[0;+\infty\right)\)
	\(\left(-\infty;0\right)\)
	\(\left(0;+\infty\right)\)
	\(\left(-\infty;+\infty\right)\)

Xét các số thực không âm \(x\) và \(y\) thỏa mãn \(2x+y\cdot4^{x+y-1}\geq3\). Giá trị nhỏ nhất của biểu thức \(P=x^2+y^2+4x+6y\) bằng

	\(\dfrac{33}{4}\)
	\(\dfrac{65}{8}\)
	\(\dfrac{49}{8}\)
	\(\dfrac{57}{8}\)

Giá trị nhỏ nhất của hàm số \(f\left(x\right)=x^3-24x\) trên đoạn \(\left[2;19\right]\) bằng

	\(32\sqrt{2}\)
	\(-40\)
	\(-32\sqrt{2}\)
	\(-45\)

Tiệm cận ngang của đồ thị hàm số \(y=\dfrac{4x+1}{x-1}\) là

	\(y=\dfrac{1}{4}\)
	\(y=4\)
	\(y=1\)
	\(y=-1\)

Cho hàm số bậc bốn \(f\left(x\right)\) có bảng biến thiên như sau: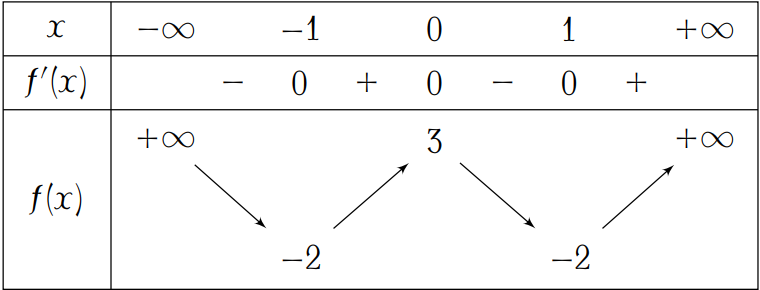

Số điểm cực trị của hàm số \(g\left(x\right)=x^4\left[f\left(x+1\right)\right]^2\) là

	\(11\)
	\(9\)
	\(7\)
	\(5\)

Tập hợp tất cả các giá trị thực của tham số \(m\) để hàm số \(y=\dfrac{x+4}{x+m}\) đồng biến trên khoảng \(\left(-\infty;-7\right)\) là

	\(\left[4;7\right)\)
	\(\left(4;7\right]\)
	\(\left(4;7\right)\)
	\(\left(4;+\infty\right)\)

Cho hàm số \(f\left(x\right)\) có bảng biến thiên như sau:

Hàm số đã cho đồng biến trên khoảng nào dưới đây?

	\(\left(-\infty;-1\right)\)
	\(\left(0;1\right)\)
	\(\left(-1;1\right)\)
	\(\left(-1;0\right)\)

Cho hàm số \(f\left(x\right)\) liên tục trên \(\mathbb{R}\) và có bảng xét dấu của \(f'\left(x\right)\) như sau:

Số điểm cực đại của hàm số đã cho là

	\(4\)
	\(1\)
	\(2\)
	\(3\)

Cho hàm \(f\left(x\right)\) có bảng biến thiên như sau:

Giá trị cực tiểu của hàm số đã cho bằng

	\(3\)
	\(-5\)
	\(0\)
	\(2\)

Cho hàm số bậc ba \(y=f(x)\) có đồ thị là đường cong trong hình.

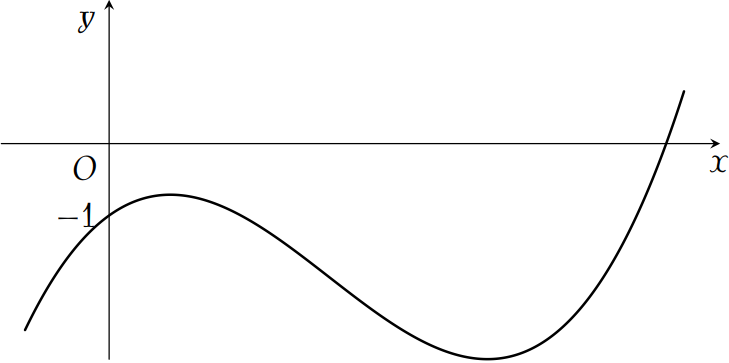
Số nghiệm thực phân biệt của phương trình \(f\left(x^3f(x)\right)+1=0\) là

	\(8\)
	\(5\)
	\(6\)
	\(4\)

Cho hàm số \(y=ax^3+bx^2+cx+d\) (\(a,\,b,\,c,\,d\in\mathbb{R}\)) có đồ thị là đường cong trong hình.

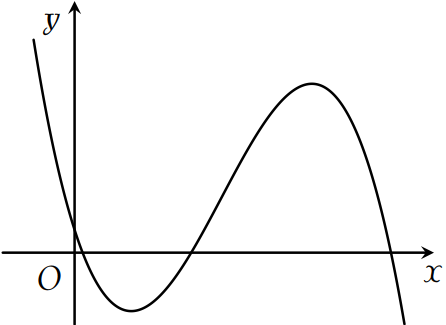
Có bao nhiêu số dương trong các số \(a\), \(b\), \(c\), \(d\)?

	\(4\)
	\(1\)
	\(2\)
	\(3\)