Cho lục giác đều $ABCDEF$ tâm $O$ (như hình).
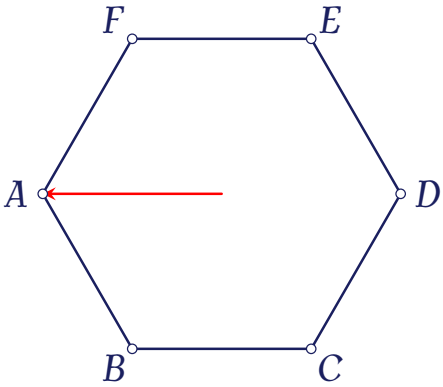
Đặt $\overrightarrow{u}=\overrightarrow{OA}$. Qua phép tịnh tiến $\mathrm{T}_{\overrightarrow{u}}$ thì
| điểm $B$ biến thành điểm $C$ | |
| điểm $C$ biến thành điểm $D$ | |
| điểm $D$ biến thành điểm $E$ | |
| điểm $E$ biến thành điểm $F$ |
Ảnh của điểm $M(-2;1)$ qua phép tịnh tiến theo vectơ $\overrightarrow{v}=(1;4)$ là điểm
| $M'(1;5)$ | |
| $M'(-1;5)$ | |
| $M'(-3;-3)$ | |
| $M'(3;-3)$ |
Trong mặt phẳng $Oxy$ cho đường tròn $(\mathscr{C})\colon(x-1)^2+(y+2)^2=4$. Phép tịnh tiến theo vectơ $\overrightarrow{v}$ biến $(\mathscr{C})$ thành đường tròn có bán kính bằng
| $2$ | |
| $4$ | |
| $16$ | |
| $8$ |
Cho hai điểm $A,\,B$ sao cho $\overrightarrow{AB}$ và $\overrightarrow{v}$ không cùng phương. Phép tịnh tiến $\mathrm{T}_{\overrightarrow{v}}$ biến hai điểm $A,\,B$ lần lượt thành $A',\,B'$. Mệnh đề nào sau đây không đúng?
| $ABB'A'$ là hình bình hành | |
| $ABA'B'$ là hình bình hành | |
| $\overrightarrow{AB}=\overrightarrow{A'B'}$ | |
| $\overrightarrow{AA'}=\overrightarrow{BB'}$ |
Ảnh của điểm $M(0;1)$ qua phép tịnh tiến theo vectơ $\overrightarrow{u}=(1;2)$ là điểm nào sau đây?
| $M'(2;3)$ | |
| $M'(1;3)$ | |
| $M'(1;1)$ | |
| $M'(-1;-1)$ |
Cho tam giác $ABC$ có $M,\,N,\,P$ lần lượt là trung điểm các cạnh $BC$, $CA$, $AB$.
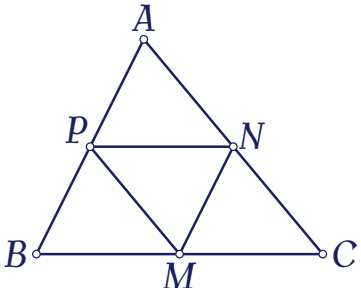
Phép tịnh tiến theo vectơ $\overrightarrow{v}=\dfrac{1}{2}\overrightarrow{BC}$ biến
| điểm $P$ thành điểm $N$ | |
| điểm $N$ thành điểm $P$ | |
| điểm $M$ thành điểm $B$ | |
| điểm $M$ thành điểm $N$ |
Phép vị tự tâm $O$ tỉ số $k=-3$ biến đường tròn $\left(\mathscr{C}\right)\colon(x-1)^2+(y+1)^2=1$ thành đường tròn có phương trình là
| $(x-1)^2+(y+1)^2=9$ | |
| $(x+3)^2+(y-3)^2=1$ | |
| $(x-3)^2+(y+3)^2=9$ | |
| $(x+3)^2+(y-3)^2=9$ |
Trong mặt phẳng tọa độ $Oxy$, cho đường tròn $\left(\mathscr{C}\right)\colon x^2+y^2+2x-4y-2=0$. Gọi $\left(\mathscr{C}'\right)$ là ảnh của $\left(\mathscr{C}\right)$ qua phép vị tự tâm $O$ tỉ số $k=-2$. Khi đó diện tích của $\left(\mathscr{C}'\right)$ bằng
| $7\pi$ | |
| $4\sqrt{7}\pi$ | |
| $28\pi$ | |
| $28\pi^2$ |
Trong mặt phẳng tọa độ $Oxy$, cho đường tròn $\left(\mathscr{C}\right)\colon(x-3)^2+y^2=9$. Ảnh của $\left(\mathscr{C}\right)$ qua phép vị tự $V_{(O,-2)}$ là đường tròn có bán kính bằng
| $9$ | |
| $6$ | |
| $18$ | |
| $36$ |
Phép vị tự tâm $O$ tỉ số $2$ biến điểm $A(-2;1)$ thành điểm $A'$. Tìm tọa độ của $A'$.
| $A'(-4;2)$ | |
| $A'\left(-2;\dfrac{1}{2}\right)$ | |
| $A'(4;-2)$ | |
| $A'\left(2;-\dfrac{1}{2}\right)$ |
Cho tam giác $HPS$ có góc $\widehat{HPS}=39^\circ$. Xét phép vị tự tâm $I$, tỉ số $k=-3$ với $I\neq P$. Biết phép vị tự trên biến $\triangle HPS$ thành $\triangle H'P'S'$. Tính số đo góc $\widehat{H'P'S'}$.
| $\widehat{H'P'S'}=39^\circ$ | |
| $\widehat{H'P'S'}=117^\circ$ | |
| $\widehat{H'P'S'}=-117^\circ$ | |
| $\widehat{H'P'S'}=13^\circ$ |
Một hình vuông có diện tích bằng $4$. Qua phép vị tự $V_{(I,-2)}$ thì ảnh của hình vuông trên có diện tích tăng gấp mấy lần diện tích ban đầu?
| $\dfrac{1}{2}$ | |
| $2$ | |
| $4$ | |
| $8$ |
Phép vị tự tâm $O$ tỉ số $-3$ lần lượt biến hai điểm $A,\,B$ thành hai điểm $C,\,D$. Mệnh đề nào sau đây đúng?
| $\overrightarrow{AC}=-3\overrightarrow{BD}$ | |
| $3\overrightarrow{AB}=\overrightarrow{DC}$ | |
| $\overrightarrow{AB}=-3\overrightarrow{CD}$ | |
| $\overrightarrow{AB}=\dfrac{1}{3}\overrightarrow{CD}$ |
Cho hai đường thẳng cắt nhau $d$ và $d'$. Có bao nhiêu phép vị tự biến $d$ thành đường thẳng $d'$?
| $0$ | |
| $1$ | |
| $2$ | |
| Vô số |
Trong mặt phẳng \(Oxy\) cho đường tròn \((x-8)^2+(y-3)^2=7\). Ảnh của đường tròn qua phép quay tâm \(O\) góc \(90^\circ\) là
| \((x+3)^2+(y-8)^2=4\) | |
| \((x+8)^2+(y-3)^2=7\) | |
| \((x+8)^2+(y+3)^2=7\) | |
| \((x+3)^2+(y-8)^2=7\) |
Gọi \(N\) là ảnh của điểm \(M=\left(-6;1\right)\) qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay \(\mathrm{Q}_{\left(O,90^\circ\right)}\) và phép vị tự tâm \(O\) tỉ số \(k=2\). Tọa độ điểm \(N\) là
| \(N=\left(-2;-12\right)\) | |
| \(N=\left(2;12\right)\) | |
| \(N=\left(-12;-2\right)\) | |
| \(N=\left(12;2\right)\) |
Cho \(d\colon2x+y-3=0\). Phép vị tự tâm \(O\) tỉ số \(2\) biến đường thẳng \(d\) thành
| \(2x+y+3=0\) | |
| \(4x+2y-3=0\) | |
| \(2x+y-6=0\) | |
| \(4x+2y-5=0\) |
Trong mặt phẳng \(Oxy\), ảnh của điểm \(M\left(-6;1\right)\) qua phép quay \(\mathrm{Q}_{\left(O,90^\circ\right)}\) là
| \(M'\left(1;6\right)\) | |
| \(M'\left(-1;-6\right)\) | |
| \(M'\left(-6;-1\right)\) | |
| \(M'\left(6;1\right)\) |
Tìm ảnh của điểm \(M=(2;5)\) qua phép tịnh tiến theo vectơ \(\overrightarrow{u}=(-3;1)\).
| \(M'=\left(-1;6\right)\) | |
| \(M'=\left(-2;7\right)\) | |
| \(M'=\left(7;-2\right)\) | |
| \(M'=\left(-6;5\right)\) |
Biểu thức tọa độ của phép quay \(\mathrm{Q}_{\left(O,-90^\circ\right)}\) là
| \(\begin{cases}x'=-y\\ y'=x\end{cases}\) | |
| \(\begin{cases}x'=x\\ y'=-y\end{cases}\) | |
| \(\begin{cases}x'=-x\\ y'=y\end{cases}\) | |
| \(\begin{cases}x'=y\\ y'=-x\end{cases}\) |
