Đồ thị của hàm số nào dưới đây có tiệm cận đứng?

	\(y=\dfrac{\sqrt{1-x^2}+1}{2019}\)
	\(y=\dfrac{x^2-1}{x-1}\)
	\(y=\dfrac{x^2}{x^2+2018}\)
	\(y=\dfrac{x}{x+12}\)

Đồ thị của hàm số nào sau đây nhận đường thẳng \(x=2\) làm tiệm cận đứng?

	\(y=\dfrac{1}{x+1}\)
	\(y=\dfrac{5x}{2-x}\)
	\(y=x-2+\dfrac{1}{x+1}\)
	\(y=\dfrac{1}{x+2}\)

Đường tiệm cận đứng của đồ thị hàm số \(y=\dfrac{7-2x}{x-2}\) là

	\(x=-3\)
	\(x=2\)
	\(x=-2\)
	\(x=3\)

Đường tiệm cận đứng của đồ thị hàm số \(y=\dfrac{3x-5}{x-2}\) là

	\(x=2\)
	\(y=2\)
	\(x=3\)
	\(x=\dfrac{5}{3}\)

Đồ thị hàm số \(y=\dfrac{2020x-2021}{x+1}\) có đường tiệm cận đứng là

	\(x=2020\)
	\(x=2021\)
	\(x=-1\)
	\(y=-1\)

Đồ thị của hàm số nào dưới đây có đường tiệm cận ngang?

	\(y=\dfrac{3x^2-1}{x+1}\)
	\(y=x^4-x^2-2\)
	\(y=\dfrac{2-x}{x}\)
	\(y=x^3-x^2+x-3\)

Đường thẳng \(y=2\) là tiệm cận ngang của đồ thị hàm số nào dưới đây?

	\(y=\dfrac{2x-1}{1-x}\)
	\(y=\dfrac{4x-1}{2x+5}\)
	\(y=\dfrac{x+1}{2x+1}\)
	\(y=\dfrac{2x-4}{2x+3}\)

Đồ thị hàm số \(f(x)=x^3+2x^2+3x+2021\) có bao nhiêu đường tiệm cận ngang?

	\(0\)
	\(1\)
	\(2\)
	\(3\)

Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số \(y=\dfrac{1-4x}{2x-1}\)?

	\(y=2\)
	\(y=\dfrac{1}{2}\)
	\(y=4\)
	\(y=-2\)

Tìm tiệm cận ngang của đồ thị hàm số \(f(x)=1+\dfrac{2x+2}{x-1}\).

	\(x=1\)
	\(y=1\)
	\(y=2\)
	\(y=3\)

Đường tiệm cận ngang của đồ thị hàm số \(y=\dfrac{2-2x}{x+1}\) là

	\(y=-2\)
	\(x=-1\)
	\(x=-2\)
	\(y=2\)

Đường tiệm cận ngang của đồ thị hàm số \(y=\dfrac{x-3}{x-1}\) là

	\(y=5\)
	\(y=0\)
	\(x=1\)
	\(y=1\)

Đường tiệm cận ngang của đồ thị hàm số \(y=\dfrac{2x-3}{x+4}\) là

	\(x=-4\)
	\(y=2\)
	\(x=4\)
	\(y=-\dfrac{3}{4}\)

Giá trị nhỏ nhất của hàm số \(f\left(x\right)=x^3-24x\) trên đoạn \(\left[2;19\right]\) bằng

	\(32\sqrt{2}\)
	\(-40\)
	\(-32\sqrt{2}\)
	\(-45\)

Tiệm cận ngang của đồ thị hàm số \(y=\dfrac{4x+1}{x-1}\) là

	\(y=\dfrac{1}{4}\)
	\(y=4\)
	\(y=1\)
	\(y=-1\)

Cho hàm số bậc bốn \(f\left(x\right)\) có bảng biến thiên như sau: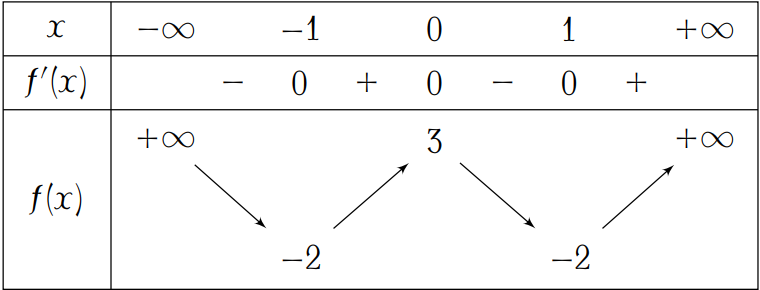

Số điểm cực trị của hàm số \(g\left(x\right)=x^4\left[f\left(x+1\right)\right]^2\) là

	\(11\)
	\(9\)
	\(7\)
	\(5\)

Tập hợp tất cả các giá trị thực của tham số \(m\) để hàm số \(y=\dfrac{x+4}{x+m}\) đồng biến trên khoảng \(\left(-\infty;-7\right)\) là

	\(\left[4;7\right)\)
	\(\left(4;7\right]\)
	\(\left(4;7\right)\)
	\(\left(4;+\infty\right)\)

Cho hàm số \(f\left(x\right)\) có bảng biến thiên như sau:

Hàm số đã cho đồng biến trên khoảng nào dưới đây?

	\(\left(-\infty;-1\right)\)
	\(\left(0;1\right)\)
	\(\left(-1;1\right)\)
	\(\left(-1;0\right)\)

Cho hàm số \(f\left(x\right)\) liên tục trên \(\mathbb{R}\) và có bảng xét dấu của \(f'\left(x\right)\) như sau:

Số điểm cực đại của hàm số đã cho là

	\(4\)
	\(1\)
	\(2\)
	\(3\)

Cho hàm \(f\left(x\right)\) có bảng biến thiên như sau:

Giá trị cực tiểu của hàm số đã cho bằng

	\(3\)
	\(-5\)
	\(0\)
	\(2\)