Trong mặt phẳng $Oxy$, cho điểm $M(1;-3)$. Ảnh của điểm M qua phép tịnh tiến theo vectơ $\overrightarrow{v}=(1;-2)$ là
| $M’(2;5)$ | |
| $M’(2;-5)$ | |
| $M’(0;-1)$ | |
| $M’(0;-5)$ |
Cho tam giác $ABC$ có $M,\,N,\,P$ lần lượt là trung điểm các cạnh $BC$, $CA$, $AB$. Phép tịnh tiến theo vectơ $\overrightarrow{v}=\dfrac{1}{2}\overrightarrow{BC}$ biến
| điểm $P$ thành điểm $N$ | |
| điểm $N$ thành điểm $P$ | |
| điểm $M$ thành điểm $B$ | |
| điểm $M$ thành điểm $N$ |
Trong mặt phẳng tọa độ $Oxy$, cho vectơ $\overrightarrow{v}=(2;1)$ và điểm $A(4;5)$. Điểm $A$ là ảnh của điểm nào sau đây qua phép tịnh tiến $\mathrm{T}_{\overrightarrow{v}}$?
| $I(2;4)$ | |
| $J(6;6)$ | |
| $K(1;-1)$ | |
| $L(-2;-4)$ |
Trong mặt phẳng tọa độ $Oxy$, cho hai điểm $A(1;6)$, $B(-1;-4)$. Gọi $C,\,D$ lần lượt là ảnh của $A,\,B$ qua phép tịnh tiến theo vectơ $\overrightarrow{v}=(1;5)$. Mệnh đề nào sau đây là đúng?
| $ABCD$ là hình thang | |
| $ABCD$ là hình bình hành | |
| $ABDC$ là hình bình hành | |
| $A,\,B,\,C,\,D$ thẳng hàng |
Phép tịnh tiến $\mathrm{T}_{\overrightarrow{v}}$ biến hai điểm $A,\,B$ lần lượt thành $A',\,B'$. Mệnh đề nào sau đây là đúng?
| $ABB'A'$ là hình bình hành | |
| $ABA'B'$ là hình bình hành | |
| $\overrightarrow{AB}=2\overrightarrow{A'B'}$ | |
| $\overrightarrow{AA'}=\overrightarrow{BB'}$ |
Cho hình bình hành $ABCD$. Phép tịnh tiến theo vectơ nào sau đây biến đường thẳng $AB$ thành đường thẳng $CD$ và biến đường thẳng $AD$ thành đường thẳng $BC$?
| $\overrightarrow{AC}$ | |
| $\overrightarrow{CA}$ | |
| $\overrightarrow{BD}$ | |
| $\overrightarrow{DB}$ |
Cho lục giác đều $ABCDEF$ tâm $O$ (như hình).
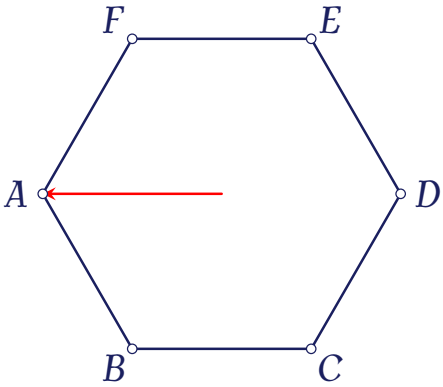
Đặt $\overrightarrow{u}=\overrightarrow{OA}$. Qua phép tịnh tiến $\mathrm{T}_{\overrightarrow{u}}$ thì
| điểm $B$ biến thành điểm $C$ | |
| điểm $C$ biến thành điểm $D$ | |
| điểm $D$ biến thành điểm $E$ | |
| điểm $E$ biến thành điểm $F$ |
Ảnh của điểm $M(-2;1)$ qua phép tịnh tiến theo vectơ $\overrightarrow{v}=(1;4)$ là điểm
| $M'(1;5)$ | |
| $M'(-1;5)$ | |
| $M'(-3;-3)$ | |
| $M'(3;-3)$ |
Cho hai điểm $A,\,B$ sao cho $\overrightarrow{AB}$ và $\overrightarrow{v}$ không cùng phương. Phép tịnh tiến $\mathrm{T}_{\overrightarrow{v}}$ biến hai điểm $A,\,B$ lần lượt thành $A',\,B'$. Mệnh đề nào sau đây không đúng?
| $ABB'A'$ là hình bình hành | |
| $ABA'B'$ là hình bình hành | |
| $\overrightarrow{AB}=\overrightarrow{A'B'}$ | |
| $\overrightarrow{AA'}=\overrightarrow{BB'}$ |
Ảnh của điểm $M(0;1)$ qua phép tịnh tiến theo vectơ $\overrightarrow{u}=(1;2)$ là điểm nào sau đây?
| $M'(2;3)$ | |
| $M'(1;3)$ | |
| $M'(1;1)$ | |
| $M'(-1;-1)$ |
Cho tam giác $ABC$ có $M,\,N,\,P$ lần lượt là trung điểm các cạnh $BC$, $CA$, $AB$.
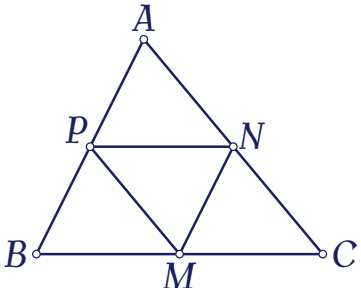
Phép tịnh tiến theo vectơ $\overrightarrow{v}=\dfrac{1}{2}\overrightarrow{BC}$ biến
| điểm $P$ thành điểm $N$ | |
| điểm $N$ thành điểm $P$ | |
| điểm $M$ thành điểm $B$ | |
| điểm $M$ thành điểm $N$ |
Tìm ảnh của điểm \(M=(2;5)\) qua phép tịnh tiến theo vectơ \(\overrightarrow{u}=(-3;1)\).
| \(M'=\left(-1;6\right)\) | |
| \(M'=\left(-2;7\right)\) | |
| \(M'=\left(7;-2\right)\) | |
| \(M'=\left(-6;5\right)\) |
Trong mặt phẳng \(Oxy\) nếu một phép tịnh tiến biến điểm \(M(4;2)\) thành điểm \(M'(4;5)\) thì phép tịnh tiến đó biến điểm \(A(2;5)\) thành điểm nào sau đây?
| \(E(5;2)\) | |
| \(F(1;6)\) | |
| \(G(2;8)\) | |
| \(H(2;5)\) |
Trong mặt phẳng \(Oxy\) cho điểm \(A(2;5)\). Hỏi \(A\) là ảnh của điểm nào trong các điểm sau qua phép tịnh tiến theo vectơ \(\overrightarrow{v}=(1;2)\)?
| \(M(1;3)\) | |
| \(N(1;6)\) | |
| \(P(3;7)\) | |
| \(Q(2;4)\) |
Trong mặt phẳng \(Oxy\) cho vectơ \(\overrightarrow{v}=(-3;2)\) và điểm \(A(1;3)\). Ảnh của điểm \(A\) qua phép tịnh tiến theo vectơ \(\overrightarrow{v}\) là điểm nào sau đây?
| \(M(-3;2)\) | |
| \(N(1;3)\) | |
| \(P(-2;5)\) | |
| \(Q(2;-5)\) |
Trong mặt phẳng \(Oxy\) cho điểm \(A(2;5)\). Phép tịnh tiến theo vectơ \(\overrightarrow{v}=(1;2)\) biến \(A\) thành điểm \(A'\) có tọa độ là
| \((3;1)\) | |
| \((1;6)\) | |
| \((3;7)\) | |
| \((4;7)\) |
Cho hình bình hành \(ABCD\). Có bao nhiêu phép tịnh tiến biến đường thẳng \(AB\) thành đường thẳng \(CD\) và biến đường thẳng \(AD\) thành đường thẳng \(BC\)?
| \(0\) | |
| \(1\) | |
| \(2\) | |
| Vô số |
Trong mặt phẳng $Oxy$, cho đường tròn $\left(\mathscr{C}\right)\colon(x+3)^2+(y-1)^2=5$ và $\overrightarrow{v}=(2;1)$. Viết phương trình đường tròn $(\mathscr{C}’)$ là ảnh của $(\mathscr{C})$ qua phép tịnh tiến theo vectơ $\overrightarrow{v}$.
Trong mặt phẳng $Oxy$, phép quay tâm $O$ góc quay $-90^\circ$ biến $M(-3;5)$ thành điểm có tọa độ
| $(-5;-3)$ | |
| $(5;-3)$ | |
| $(5;3)$ | |
| $(-5;3)$ |
Trong mặt phẳng $Oxy$, cho điểm $A(1;0)$. Ảnh của $A$ qua phép quay tâm $O$ góc quay $90^\circ$ là
| $A’(0;-1)$ | |
| $A’(-1;0)$ | |
| $A’(0;1)$ | |
| $A’(1;1)$ |
