Tập xác định của hàm số $y=\dfrac{x+1}{x-1}$ là
| $\mathscr{D}=\mathbb{R}\setminus\{1\}$ | |
| $\mathscr{D}=\mathbb{R}\setminus\{-1\}$ | |
| $\mathscr{D}=\mathbb{R}\setminus\{\pm1\}$ | |
| $\mathscr{D}=(1;+\infty)$ |
Phép vị tự tâm $O$ tỉ số $k=-3$ biến đường tròn $\left(\mathscr{C}\right)\colon(x-1)^2+(y+1)^2=1$ thành đường tròn có phương trình là
| $(x-1)^2+(y+1)^2=9$ | |
| $(x+3)^2+(y-3)^2=1$ | |
| $(x-3)^2+(y+3)^2=9$ | |
| $(x+3)^2+(y-3)^2=9$ |
Trong mặt phẳng tọa độ $Oxy$, cho đường tròn $\left(\mathscr{C}\right)\colon x^2+y^2+2x-4y-2=0$. Gọi $\left(\mathscr{C}'\right)$ là ảnh của $\left(\mathscr{C}\right)$ qua phép vị tự tâm $O$ tỉ số $k=-2$. Khi đó diện tích của $\left(\mathscr{C}'\right)$ bằng
| $7\pi$ | |
| $4\sqrt{7}\pi$ | |
| $28\pi$ | |
| $28\pi^2$ |
Trong mặt phẳng tọa độ $Oxy$, cho đường tròn $\left(\mathscr{C}\right)\colon(x-3)^2+y^2=9$. Ảnh của $\left(\mathscr{C}\right)$ qua phép vị tự $V_{(O,-2)}$ là đường tròn có bán kính bằng
| $9$ | |
| $6$ | |
| $18$ | |
| $36$ |
Phép vị tự tâm $O$ tỉ số $2$ biến điểm $A(-2;1)$ thành điểm $A'$. Tìm tọa độ của $A'$.
| $A'(-4;2)$ | |
| $A'\left(-2;\dfrac{1}{2}\right)$ | |
| $A'(4;-2)$ | |
| $A'\left(2;-\dfrac{1}{2}\right)$ |
Cho tam giác $HPS$ có góc $\widehat{HPS}=39^\circ$. Xét phép vị tự tâm $I$, tỉ số $k=-3$ với $I\neq P$. Biết phép vị tự trên biến $\triangle HPS$ thành $\triangle H'P'S'$. Tính số đo góc $\widehat{H'P'S'}$.
| $\widehat{H'P'S'}=39^\circ$ | |
| $\widehat{H'P'S'}=117^\circ$ | |
| $\widehat{H'P'S'}=-117^\circ$ | |
| $\widehat{H'P'S'}=13^\circ$ |
Một hình vuông có diện tích bằng $4$. Qua phép vị tự $V_{(I,-2)}$ thì ảnh của hình vuông trên có diện tích tăng gấp mấy lần diện tích ban đầu?
| $\dfrac{1}{2}$ | |
| $2$ | |
| $4$ | |
| $8$ |
Phép vị tự tâm $O$ tỉ số $-3$ lần lượt biến hai điểm $A,\,B$ thành hai điểm $C,\,D$. Mệnh đề nào sau đây đúng?
| $\overrightarrow{AC}=-3\overrightarrow{BD}$ | |
| $3\overrightarrow{AB}=\overrightarrow{DC}$ | |
| $\overrightarrow{AB}=-3\overrightarrow{CD}$ | |
| $\overrightarrow{AB}=\dfrac{1}{3}\overrightarrow{CD}$ |
Cho hai đường thẳng cắt nhau $d$ và $d'$. Có bao nhiêu phép vị tự biến $d$ thành đường thẳng $d'$?
| $0$ | |
| $1$ | |
| $2$ | |
| Vô số |
Cắt khối lăng trụ $ABC.A'B'C'$ bởi mặt phẳng $\left(A'BC\right)$ ta được
| Một khối chóp tam giác và một khối chóp ngũ giác | |
| Hai khối chóp tứ giác | |
| Một khối chóp tam giác và một khối chóp tứ giác | |
| Hai khối chóp tam giác |
Cho khối lập phương $ABCD.A'B'C'D'$. Mặt phẳng $\left(BDD'B'\right)$ chia khối lập phương thành
| Hai khối lăng trụ tam giác | |
| Hai khối tứ diện | |
| Hai khối lăng trụ tứ giác | |
| Hai khối chóp tứ giác |
Có thể chia khối chóp $S.ABCD$ thành hai khối tứ diện là
| $SBCD$ và $SACD$ | |
| $SACD$ và $SABD$ | |
| $SABC$ và $SABD$ | |
| $SABC$ và $SACD$ |
Cho khối chóp có đáy là đa giác $n$ cạnh. Mệnhh đề nào sau đây là đúng?
| Số mặt của khối chóp là $2n$ | |
| Số đỉnh của khối chóp bằng $2n+1$ | |
| Số cạnh của khối chóp bằng $n+1$ | |
| Số mặt của khối chóp bằng số đỉnh của nó |
Hình lăng trụ có thể có số cạnh là số nào sau đây?
| $3000$ | |
| $3001$ | |
| $3005$ | |
| $3007$ |
Trong các hình dưới đây, hình nào không phải hình đa diện?
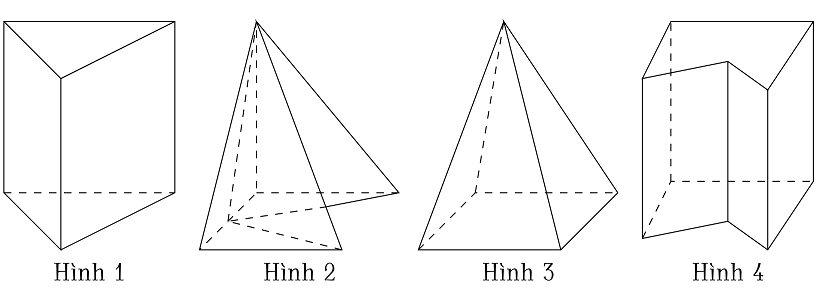
| Hình 1 | |
| Hình 2 | |
| Hình 3 | |
| Hình 4 |
Trong các hình dưới đây, hình nào không phải hình đa diện?
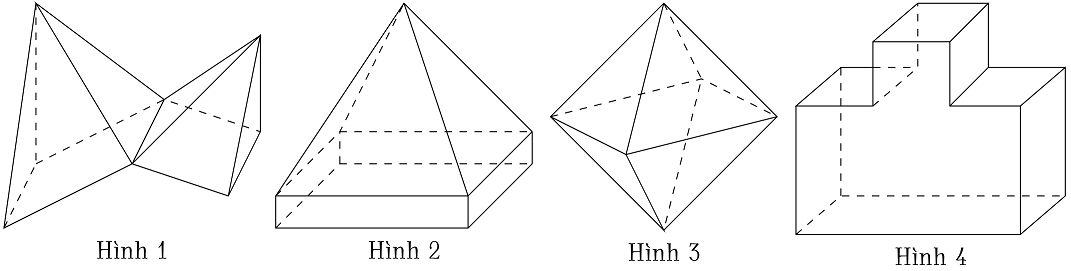
| Hình 1 | |
| Hình 2 | |
| Hình 3 | |
| Hình 4 |
Trong các hình dưới đây, hình nào là hình đa diện?
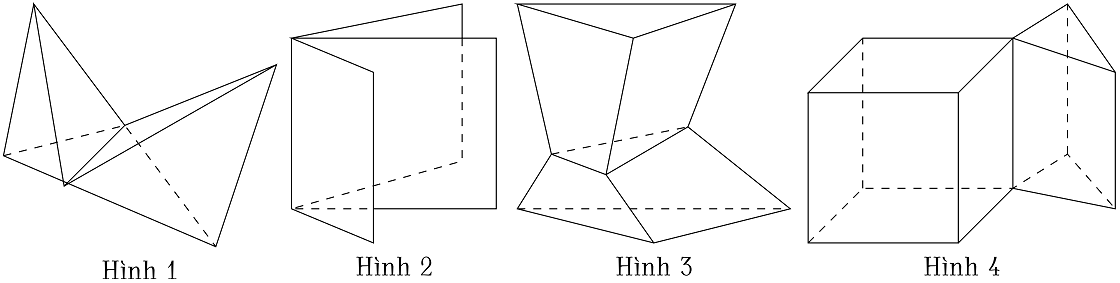
| Hình 4 | |
| Hình 2 | |
| Hình 1 | |
| Hình 3 |