Hai vectơ có cùng độ dài và ngược hướng gọi là

	Hai vectơ cùng hướng
	Hai vectơ cùng phương
	Hai vectơ bằng nhau
	Hai vectơ đối nhau

Cho hình bình hành \(ABCD\). Đẳng thức vectơ nào sau đây đúng?

	\(\overrightarrow{CD}+\overrightarrow{CB}=\overrightarrow{CA}\)
	\(\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AC}\)
	\(\overrightarrow{BA}+\overrightarrow{BD}=\overrightarrow{BC}\)
	\(\overrightarrow{CD}+\overrightarrow{AD}=\overrightarrow{AC}\)

Cho tam giác \(ABC\). Khẳng định nào sau đây đúng?

	\(\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{BC}\)
	\(\overrightarrow{AB}+\overrightarrow{CA}=\overrightarrow{CB}\)
	\(\overrightarrow{CA}+\overrightarrow{BA}=\overrightarrow{CB}\)
	\(\overrightarrow{AA}+\overrightarrow{BB}=\overrightarrow{AB}\)

Cho tam giác \(ABC\) cân tại \(A\). Phát biểu nào sau đây đúng?

	\(\overrightarrow{AB}=\overrightarrow{AC}\)
	\(\left|\overrightarrow{AB}\right|=\left|\overrightarrow{AC}\right|\)
	\(\overrightarrow{AB},\,\overrightarrow{AC}\) cùng hướng
	\(\overrightarrow{AB},\,\overrightarrow{AC}\) cùng phương

Cho tam giác đều \(ABC\) cạnh \(a\). Tìm mệnh đề đúng.

	\(\left|\overrightarrow{AB}\right|+\left|\overrightarrow{AC}\right|=a\)
	\(\left|\overrightarrow{AB}\right|+\left|\overrightarrow{AC}\right|=a\sqrt{3}\)
	\(\left|\overrightarrow{AB}\right|+\left|\overrightarrow{AC}\right|=\dfrac{a\sqrt{3}}{2}\)
	\(\left|\overrightarrow{AB}\right|+\left|\overrightarrow{AC}\right|=2a\)

Cho hai hình bình hành \(ABCD\) và \(ABEF\) có chung cạnh \(AB\).

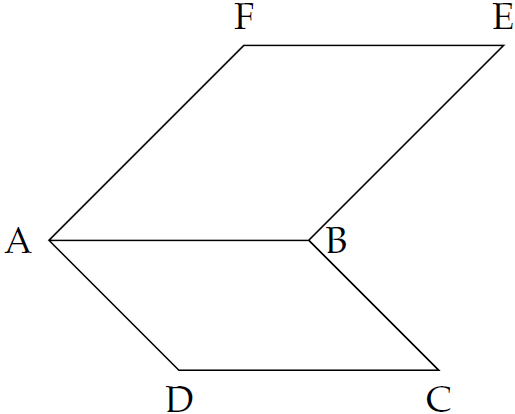
Vectơ nào sau đây bằng với vectơ \(\overrightarrow{CE}\)?

	\(\overrightarrow{AF}\)
	\(\overrightarrow{DF}\)
	\(\overrightarrow{BF}\)
	\(\overrightarrow{BD}\)

Cho hình bình hành \(ABCD\). Đẳng thức nào sau đây đúng?

	\(\overrightarrow{DA}=\overrightarrow{BC}\)
	\(\overrightarrow{AC}=\overrightarrow{BD}\)
	\(\overrightarrow{BA}=\overrightarrow{CD}\)
	\(\overrightarrow{BA}=\overrightarrow{DC}\)

Gọi \(C\) là trung điểm của đoạn thẳng \(AB\). Hãy chọn khẳng định đúng trong các khẳng định sau:

	\(\overrightarrow{CA}=\overrightarrow{CB}\)
	\(\overrightarrow{AB},\,\overrightarrow{AC}\) cùng hướng
	\(\overrightarrow{AB},\,\overrightarrow{CB}\) ngược hướng
	\(\left|\overrightarrow{AC}\right|=\overrightarrow{CB}\)

Cho hình bình hành \(ABCD\), tâm \(O\). Đẳng thức nào sau đây sai?

	\(\overrightarrow{BA}=\overrightarrow{CD}\)
	\(\left|\overrightarrow{AB}\right|=\left|\overrightarrow{CD}\right|\)
	\(\overrightarrow{OA}=\overrightarrow{OC}\)
	\(\overrightarrow{AO}=\overrightarrow{OC}\)

Cho tứ giác \(ABCD\) có \(\overrightarrow{AB}=\overrightarrow{DC}\), \(\left|\overrightarrow{AB}\right|=\left|\overrightarrow{BD}\right|\) và \(\left|\overrightarrow{AC}\right|=\left|\overrightarrow{BD}\right|\). \(ABCD\) là hình gì?

	Hình thoi
	Hình chữ nhật
	Hình bình hành
	Hình vuông

Cho tứ giác \(ABCD\) có \(\overrightarrow{AB}=\overrightarrow{DC}\) và \(\left|\overrightarrow{AC}\right|=\left|BD\right|\). \(ABCD\) là hình gì?

	Hình thoi
	Hình chữ nhật
	Hình bình hành
	Hình vuông

Cho tứ giác \(ABCD\) có \(\overrightarrow{AB}=\overrightarrow{DC}\) và \(\left|\overrightarrow{AB}\right|=\left|\overrightarrow{AD}\right|\). \(ABCD\) là hình gì?

	Hình thoi
	Hình chữ nhật
	Hình bình hành
	Hình vuông

Cho tứ giác \(ABCD\) có \(\overrightarrow{AB}=\overrightarrow{DC}\) và \(\left|\overrightarrow{AB}\right|=\left|\overrightarrow{BC}\right|\). Khẳng định nào sau đây sai?

	\(\overrightarrow{AD}=\overrightarrow{BC}\)
	\(ABCD\) là hình thoi
	\(\left|\overrightarrow{CD}\right|=\left|\overrightarrow{BC}\right|\)
	\(ABCD\) là hình thang cân

Cho tứ giác \(ABCD\) có \(\overrightarrow{AB},\,\overrightarrow{CD}\) cùng phương. \(ABCD\) là hình gì?

	Hình thoi
	Hình thang
	Hình bình hành
	Hình vuông

Cho lục giác đều \(ABCDEF\) tâm \(O\). Vectơ nào bằng với \(\overrightarrow{BA}\)?

	\(\overrightarrow{OF},\,\overrightarrow{DE},\,\overrightarrow{OC}\)
	\(\overrightarrow{CA},\,\overrightarrow{OF},\,\overrightarrow{DE}\)
	\(\overrightarrow{OF},\,\overrightarrow{DE},\,\overrightarrow{CO}\)
	\(\overrightarrow{OF},\,\overrightarrow{ED},\,\overrightarrow{OC}\)

Cho lục giác đều \(ABCDEF\) tâm \(O\). Đẳng thức nào sau đây sai?

	\(\overrightarrow{AB}=\overrightarrow{ED}\)
	\(\left|\overrightarrow{AB}\right|=\left|\overrightarrow{AF}\right|\)
	\(\overrightarrow{OD}=\overrightarrow{BC}\)
	\(\overrightarrow{OB}=\overrightarrow{OE}\)

Cho tam giác đều \(ABC\) cạnh \(a\). Mệnh đề nào sau đây là đúng?

	\(\left|\overrightarrow{AC}\right|=\overrightarrow{BC}\)
	\(\overrightarrow{AC}=a\)
	\(\overrightarrow{AB}=\overrightarrow{AC}\)
	\(\left|\overrightarrow{AB}\right|=a\)

Cho hình bình hành \(ABCD\). Đẳng thức nào dưới đây sai?

	\(\left|\overrightarrow{AC}\right|=\left|\overrightarrow{BD}\right|\)
	\(\left|\overrightarrow{BC}\right|=\left|\overrightarrow{DA}\right|\)
	\(\left|\overrightarrow{AD}\right|=\left|\overrightarrow{BC}\right|\)
	\(\left|\overrightarrow{AB}\right|=\left|\overrightarrow{CD}\right|\)

Cho tam giác \(ABC\) với \(M,\,N,\,P\) lần lượt là trung điểm các cạnh \(BC,\,CA,\,AB\). Số vectơ bằng với \(\overrightarrow{MN}\) là

	\(1\)
	\(2\)
	\(3\)
	\(6\)

Cho hình thoi \(ABCD\) cạnh \(a\) và góc \(\widehat{BAD}=60^\circ\). Đẳng thức nào sau đây đúng?

	\(\overrightarrow{AB}=\overrightarrow{AD}\)
	\(\left|\overrightarrow{BD}\right|=a\)
	\(\overrightarrow{BD}=\overrightarrow{AC}\)
	\(\overrightarrow{BC}=\overrightarrow{DA}\)