Gọi \(M\) và \(M'\) lần lượt là các điểm biểu diễn của số phức \(z\) và \(\overline{z}\). Tìm mệnh đề đúng.

	\(M,\,M'\) đối xứng nhau qua trục hoành
	\(M,\,M'\) đối xứng nhau qua trục tung
	\(M,\,M'\) đối xứng nhau qua gốc tọa độ
	Ba điểm \(O,\,M,\,M'\) thẳng hàng

Cho số phức \(z\) có điểm biểu diễn trên mặt phẳng \(Oxy\) là điểm \(M(3;-5)\). Xác định số phức liên hợp \(\overline{z}\) của \(z\).

	\(\overline{z}=-5+3\mathrm{i}\)
	\(\overline{z}=5+3\mathrm{i}\)
	\(\overline{z}=3+5\mathrm{i}\)
	\(\overline{z}=3-5\mathrm{i}\)

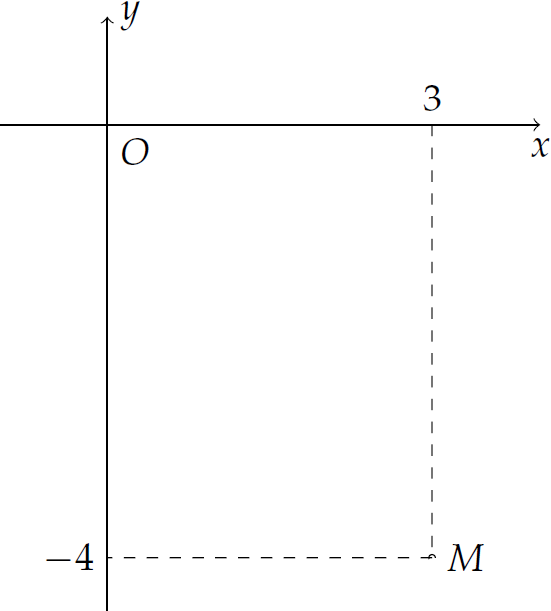
Điểm \(M\) trong hình vẽ bên biểu diễn số phức \(z\). Tìm  phần thực và phần ảo của \(z\).

	\(-4\) và \(3\)
	\(3\) và \(-4\mathrm{i}\)
	\(3\) và \(-4\)
	\(-4\) và \(3\mathrm{i}\)

Số phức nào sau đây là số thuần ảo?

	\(z=3\mathrm{i}\)
	\(z=\sqrt{3}+\mathrm{i}\)
	\(z=-2+3\mathrm{i}\)
	\(z=-2\)

Mệnh đề nào sau đây sai?

	Số phức \(z=2019\mathrm{i}\) là số thuần ảo
	Số \(2019\mathrm{i}\) không phải số thuần ảo
	Số phức \(z=5-3\mathrm{i}\) có phần thực bằng \(5\), phần ảo bằng \(-3\)
	Điểm \(M(-1;2)\) là điểm biểu diễn số phức \(z=-1+2\mathrm{i}\)

Trong các số phức \(z_1=-2\mathrm{i}\), \(z_2=2-\mathrm{i}\), \(z_3=5\mathrm{i}\), \(z_4=4\) có bao nhiêu số thuần ảo?

	\(4\)
	\(1\)
	\(3\)
	\(2\)

Tìm các số thực \(x,\,y\) thỏa mãn $$3x+y+5x\mathrm{i}=2y-1+(x-y)\mathrm{i}$$ với \(\mathrm{i}\) là đơn vị ảo.

	\(x=\dfrac{1}{7},\;y=\dfrac{4}{7}\)
	\(x=-\dfrac{2}{7},\;y=\dfrac{4}{7}\)
	\(x=-\dfrac{1}{7},\;y=\dfrac{4}{7}\)
	\(x=-\dfrac{1}{7},\;y=-\dfrac{4}{7}\)

Tìm các số thực \(x,\,y\) thỏa mãn $$(3x-2)+(2y+1)\mathrm{i}=(x+1)-(y-5)\mathrm{i}$$với \(\mathrm{i}\) là đơn vị ảo.

	\(x=\dfrac{3}{2},\;y=-2\)
	\(x=-\dfrac{3}{2},\;y=-\dfrac{4}{3}\)
	\(x=1,\;y=\dfrac{4}{3}\)
	\(x=\dfrac{3}{2},\;y=\dfrac{4}{3}\)

Tìm các số thực \(x,\,y\) thỏa mãn $$(2x+5y)+(4x+3y)\mathrm{i}=5+2\mathrm{i}$$

	\(x=\dfrac{5}{14},\;y=-\dfrac{8}{7}\)
	\(x=\dfrac{8}{7},\;y=-\dfrac{5}{14}\)
	\(x=-\dfrac{5}{14},\;y=\dfrac{8}{7}\)
	\(x=-\dfrac{5}{14},\;y=-\dfrac{8}{7}\)

Tìm các số thực \(a,\,b\) thỏa mãn $$(a-2b)+(a+b+4)\mathrm{i}=(2a+b)+2b\mathrm{i}$$ với \(\mathrm{i}\) là đơn vị ảo.

	\(a=-3,\;b=1\)
	\(a=3,\;b=-1\)
	\(a=-3,\;b=-1\)
	\(a=3,\;b=1\)

Cho \(a,\,b\) là hai số thực thỏa mãn \(2a+(b-3)\mathrm{i}=4-5\mathrm{i}\) với \(\mathrm{i}\) là đơn vị ảo. Giá trị của \(a,\,b\) bằng

	\(a=1,\;b=8\)
	\(a=8,\;b=8\)
	\(a=2,\;b=-2\)
	\(a=-2,\;b=2\)

Cho hai số phức \(z_1=-1+2\mathrm{i}\) và \(z_2=-1-2\mathrm{i}\). Giá trị của biểu thức \(\left|z_1\right|^2+\left|z_2\right|^2\) bằng

	\(\sqrt{10}\)
	\(10\)
	\(-6\)
	\(4\)

Môđun của số phức \(w=2-\sqrt{5}\mathrm{i}\) là

	\(|w|=\sqrt{29}\)
	\(|w|=1\)
	\(|w|=\sqrt{7}\)
	\(|w|=3\)

Cho số phức \(z=3+\mathrm{i}\). Tính \(\left|\overline{z}\right|\).

	\(\left|\overline{z}\right|=4\)
	\(\left|\overline{z}\right|=\sqrt{10}\)
	\(\left|\overline{z}\right|=2\sqrt{2}\)
	\(\left|\overline{z}\right|=2\)

Cho số phức \(z=-12+5\mathrm{i}\). Môđun của \(z\) bằng

	\(13\)
	\(119\)
	\(17\)
	\(-7\)

Môđun của số phức \(z=b\mathrm{i},\;b\in\mathbb{R}\) là

	\(b\)
	\(b^2\)
	\(|b|\)
	\(\sqrt{b}\)

Khẳng định nào sau đây là sai?

	Môđun của số phức \(z\) là một số âm
	Môđun của số phức \(z\) là một số thực
	Môđun của số phức \(z=a+b\mathrm{i}\) là \(|z|=\sqrt{a^2+b^2}\)
	Môđun của số phức \(z\) là một số thực không âm

Gọi \(a,\,b\) lần lượt là phần thực và phần ảo của số phức \(z=-3+2\mathrm{i}\). Giá trị của \(a+2b\) bằng

	\(1\)
	\(-1\)
	\(-4\)
	\(-7\)

Tổng phần thực và phần ảo của số phức \(z=3-\mathrm{i}\) bằng

	\(2\)
	\(-1\)
	\(-2\)
	\(3\)

Số phức liên hợp của số phức \(z=4\mathrm{i}-7\) có phần ảo là

	\(-4\)
	\(-7\)
	\(7\)
	\(4\)