Trong không gian, cho 4 điểm không đồng phẳng. Có thể xác định được bao nhiêu mặt phẳng phân biệt từ các điểm đã cho?
 | $6$ |
 | $4$ |
 | $3$ |
 | $2$ |
Trong các khẳng định sau, khẳng định nào đúng?
| Qua 2 điểm phân biệt có duy nhất một mặt phẳng |
| Qua 3 điểm phân biệt bất kì có duy nhất một mặt phẳng |
| Qua 3 điểm không thẳng hàng có duy nhất một mặt phẳng |
| Qua 4 điểm phân biệt bất kì có duy nhất một mặt phẳng |
Trền bàn có một cốc nước hình trụ chứa đầy nước, có chiều cao bằng 3 lần đường kính của đáy; một viên bi và một khối nón đều bằng thủy tinh. Biết viên bi là một khối cầu có đường kính bằng đường kính của cốc nước. Người ta từ từ thả vào cốc nước viên bi và khối nón sao cho đỉnh khối nón nằm trên mặt cầu (như hình vẽ) thì thấy nước trong cốc tràn ra ngoài.
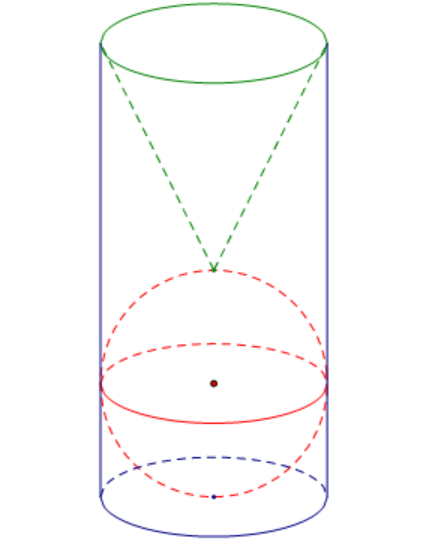
Tính tỉ số thể tích của lượng nước còn lại trong cốc và lượng nước ban đầu (bỏ qua bề dày của lớp vỏ thủy tinh).
Cho tứ diện đều \(ABCD\) cạnh \(a\). Xác định tâm và bán kính mặt cầu ngoại tiếp tứ diện.
Trong mặt phẳng $Oxy$, cho các điểm $A(1;3)$, $B(4;0)$, $C(2;-5)$. Tọa độ điểm $M$ thỏa mãn $\overrightarrow{MA}+\overrightarrow{MB}-3\overrightarrow{MC}=\overrightarrow{0}$ là
| $M\left(1;18\right)$ |
| $M\left(-1;18\right)$ |
| $M\left(1;-18\right)$ |
| $M\left(-18;1\right)$ |
Trong mặt phẳng $Oxy$, cho tam giác $MNP$ có $M(-2;1)$, $N(1;3)$, $P(0;2)$. Tọa độ trọng tâm $G$ của tam giác $MNP$ là
| $(2;1)$ |
| $\left(2;\dfrac{-1}{3}\right)$ |
| $\left(-\dfrac{1}{3};2\right)$ |
| $(1;2)$ |
Trong mặt phẳng $Oxy$, cho bốn điểm $A(2;5)$, $B(1;7)$, $C(1;5)$, $D(0;9)$. Ba điểm nào sau đây thẳng hàng?
| $A,\,B,\,D$ |
| $A,\,B,\,C$ |
| $B,\,C,\,D$ |
| $A,\,C,\,D$ |
Trong mặt phẳng $Oxy$, cho hình thang $ABCD$ có đáy lớn $CD$ gấp đôi đáy nhỏ $AB$. Biết $A(1;1)$, $B(-1;2)$, $C(0;1)$. Tọa độ điểm $D$ là
| $D(4;-1)$ |
| $D(-4;-1)$ |
| $D(4;1)$ |
| $D(-4;1)$ |
Trong mặt phẳng $Oxy$, cho $A(2;5)$, $B(1;3)$, $C(5;-1)$. Tọa độ trọng tâm $G$ của tam giác $ABC$ là
| $G(8;7)$ |
| $G\left(\dfrac{8}{3};\dfrac{7}{3}\right)$ |
| $G\left(-\dfrac{8}{3};-\dfrac{7}{3}\right)$ |
| $G\left(-\dfrac{8}{3};\dfrac{7}{3}\right)$ |
Trong mặt phẳng $Oxy$, cho $2$ điểm $A\left(2;-5\right)$, $B\left(-1;3\right)$. Tọa độ vectơ $\overrightarrow{AB}$ là
| $\overrightarrow{AB}=\left(1;-2\right)$ |
| $\overrightarrow{AB}=\left(-3;8\right)$ |
| $\overrightarrow{AB}=\left(3;-8\right)$ |
| $\overrightarrow{AB}=\left(-2;-15\right)$ |
Trong mặt phẳng $Oxy$, cho hai điểm $A\left(1;0\right)$ và $B\left(0;-2\right)$. Tọa độ trung điểm của đoạn thẳng $AB$ là
| $\left(\dfrac{1}{2};-1\right)$ |
| $\left(-1;\dfrac{1}{2}\right)$ |
| $\left(\dfrac{1}{2};-2\right)$ |
| $\left(1;-1\right)$ |
Trong mặt phẳng $Oxy$, cho tam giác $ABC$ có trọng tâm là gốc tọa độ $O$ hai đỉnh $A\left(-2;2\right)$ và $B\left(3;5\right)$. Tọa độ đỉnh $C$ là
| $\left(-1;-7\right)$ |
| $\left(2;-2\right)$ |
| $\left(-3;-5\right)$ |
| $\left(1;7\right)$ |
Trong mặt phẳng $Oxy$, cho hai điểm $A(-3;2)$, $B(1;4)$. Tìm tọa độ điểm $M$ thỏa mãn $\overrightarrow{AM}=-2\overrightarrow{AB}$.
| $M(6;-2)$ |
| $M(3;8)$ |
| $M(8;-4)$ |
| $M(-11;-2)$ |
Trong mặt phẳng $Oxy$, cho các vectơ $\overrightarrow{a}=(0;1)$, $\overrightarrow{b}=(-1;2)$, $\overrightarrow{c}=(-3;-2)$. Tọa độ của vectơ $\overrightarrow{u}=3\overrightarrow{a}+2\overrightarrow{b}-4\overrightarrow{c}$ là
| $(10;-15)$ |
| $(15;10)$ |
| $(10;15)$ |
| $(-10;15)$ |
Trong mặt phẳng $Oxy$, cho tam giác $ABC$ có $A(2;1)$, $B(-1;2)$, $C(3;0)$. Tứ giác $ABCD$ là hình bình hành khi tọa độ đỉnh $D$ là cặp số nào dưới đây?
| $(0;-1)$ |
| $(6;-1)$ |
| $(1;6)$ |
| $(-6;1)$ |
Trong mặt phẳng $Oxy$, cho hai vectơ $\overrightarrow{a}=(2;-4)$, $\overrightarrow{b}=(-5;3)$. Tìm tọa độ của vectơ $\overrightarrow{x}=2\overrightarrow{a}-\overrightarrow{b}$.
| $\overrightarrow{x}=(7;-7)$ |
| $\overrightarrow{x}=(9;5)$ |
| $\overrightarrow{x}=(9;-11)$ |
| $\overrightarrow{x}=(-1;5)$ |
Trong mặt phẳng $Oxy$, cho các vectơ $\overrightarrow{u}=(3;-2)$ và $\overrightarrow{v}=\left(m^2;4\right)$ với $m$ là số thực. Tìm $m$ để $\overrightarrow{u}$ và $\overrightarrow{v}$ cùng phương.
| $m=\sqrt{6}$ |
| $m=-6$ |
| Không có giá trị nào của $m$ |
| $m=\pm\sqrt{6}$ |
Trong mặt phẳng $Oxy$, cho hai điểm $A(-1;2)$ và $B(3;-4)$. Tọa độ của vectơ $\overrightarrow{AB}$ là
| $(-4;6)$ |
| $(4;-6)$ |
| $(2;-3)$ |
| $(3;-2)$ |
Trong mặt phẳng $Oxy$, cho $\overrightarrow{a}=(3;-4)$, $\overrightarrow{b}=(-1;2)$. Tọa độ của $\overrightarrow{a}+\overrightarrow{b}$ là
| $(-4;6)$ |
| $(2;-2)$ |
| $(4;-6)$ |
| $(-3;-8)$ |
Trong mặt phẳng $Oxy$, cho tam giác $ABC$ có $A\left(-1;3\right)$, $B\left(2;3\right)$, $C\left(5;-3\right)$. Tọa độ trọng tâm $G$ của tam giác $ABC$ là
| $\left(2;1\right)$ |
| $\left(2;3\right)$ |
| $\left(\dfrac{1}{2};0\right)$ |
| $\left(-\dfrac{8}{3};1\right)$ |