Cho hàm số $f(x)=\left|x^4-4x^3+4x^2+a\right|$. Gọi $M,\,m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn $[0;2]$. Có bao nhiêu số nguyên $a$ thuộc đoạn $[-3;2]$ sao cho $M\leq2m$?
| $7$ | |
| $5$ | |
| $6$ | |
| $4$ |
Giá trị nhỏ nhất của hàm số $y=\dfrac{2\sin x+3}{\sin x+1}$ trên $\left[0;\dfrac{\pi}{2}\right]$ là
| $5$ | |
| $2$ | |
| $3$ | |
| $\dfrac{5}{2}$ |
Tìm giá trị nhỏ nhất $m$ của hàm số $y=x^4-x^2+13$ trên đoạn $[-2;3]$.
| $m=13$ | |
| $m=\dfrac{51}{4}$ | |
| $m=\dfrac{49}{4}$ | |
| $m=\dfrac{205}{16}$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
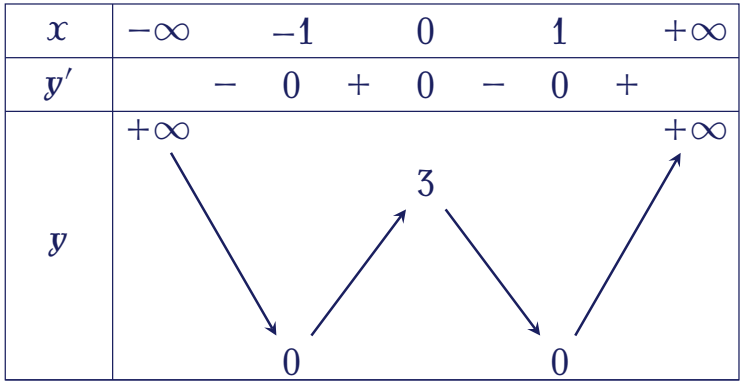
Giá trị lớn nhất của hàm số $y=f(x)$ trên đoạn $[-1;1]$ bằng
| $1$ | |
| $3$ | |
| $-1$ | |
| $0$ |
Cho hàm số $f(x)=x^3+ax^2+bx+c$ có đồ thị $\left(\mathscr{C}\right)$. Mệnh đề nào sau đây sai?
| Đồ thị $\left(\mathscr{C}\right)$ luôn có tâm đối xứng | |
| Hàm số $f(x)$ luôn có cực trị | |
| Đồ thị $\left(\mathscr{C}\right)$ luôn cắt trục hoành | |
| $\lim\limits_{x\to+\infty}f(x)=+\infty$ |
Số điểm cực trị của hàm số $y=\dfrac{1}{3}x^3-2x^2+4$ là
| $0$ | |
| $1$ | |
| $2$ | |
| $3$ |
Giá trị cực tiểu $y_{CT}$ của hàm số $y=x^3-3x^2+2$ là
| $y_{CT}=0$ | |
| $y_{CT}=-2$ | |
| $y_{CT}=1$ | |
| $y_{CT}=4$ |
Hình bên là đồ thị hàm số $y=f'(x)$.
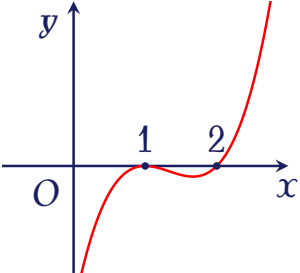
Hỏi hàm số $y=f(x)$ đồng biến trên khoảng nào dưới đây?
| $(0;1)$ và $(2;+\infty)$ | |
| $(1;2)$ | |
| $(2;+\infty)$ | |
| $(0;1)$ |
Hàm số nào sau đây đồng biến trên $\mathbb{R}$?
| $y=\dfrac{x-1}{x+3}$ | |
| $y=-x^3-x-2$ | |
| $y=x^4+2x^2+3$ | |
| $y=x^3+x^2+2x+1$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
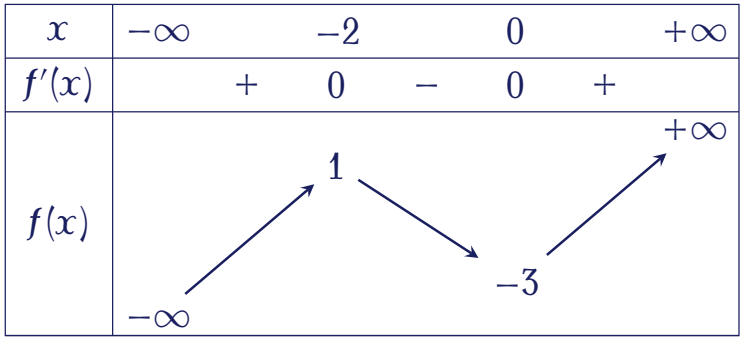
Hàm số $y=f(x)$ nghịch biến trên khoảng nào dưới đây?
| $(-3;1)$ | |
| $(0;+\infty)$ | |
| $(-\infty;-2)$ | |
| $(-2;0)$ |
Cho tứ diện $ABCD$. Gọi $M$ và $N$ lần lượt là trung điểm của $AC$ và $BC$. $P$ là điểm di động trên đoạn $BD$. Mặt phẳng $(MNP)$ cắt $AD$ tại $Q$.
- Tứ giác $MNPQ$ là hình gì?
- Tìm tập hợp giao điểm $I$ của $MQ$ và $NP$ khi $P$ di động trên đoạn $BD$.
Cho tứ diện $ABCD$, gọi $E$ là trung điểm của $AB$. Giao tuyến của hai mặt phẳng $(ECD)$ và $(ABC)$ là
| $ED$ | |
| $EC$ | |
| $EB$ | |
| $EA$ |
Cho tứ diện $ABCD$, $M$ là trung điểm của $AB$, $N$ là điểm trên $AC$ mà $AN=\dfrac{1}{4}AC$, $P$ là điểm trên đoạn $AD$ mà $AP=\dfrac{2}{3}AD$. Gọi $E$ là giao điểm của $MP$ và $BD$, $F$ là giao điểm của $MN$ và $BC$. Khi đó giao tuyến của $(BCD)$ và $(MPC)$ là
| $CE$ | |
| $MF$ | |
| $NE$ | |
| $CP$ |
Cho tứ diện $ABCD$. $M$ là điểm nằm trong tam giác $ABC$, $(\alpha)$ qua $M$ và song song với $AB$ và $CD$. Thiết diện của $ABCD$ cắt bởi $(\alpha)$ là
| Tam giác | |
| Hình bình hành | |
| Hình vuông | |
| Hình chữ nhật |
Cho hai đường thẳng chéo nhau $a$ và $b$. Lấy $A,\,B$ thuộc $a$ và $C,\,D$ thuộc $b$. Khẳng định nào sau đây đúng khi nói về hai đường thẳng $AD$ và $BC$?
| Cắt nhau | |
| Có thể song song hoặc cắt nhau | |
| Chéo nhau | |
| Song song nhau |
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành. Gọi $N,\,P$ lần lượt là trung điểm của các cạnh $BC,\,AD$; $K$ là giao $BP$ và $AN$. Khi đó $SK$ là giao tuyến của mặt phẳng $(SAN)$ và mặt phẳng nào sau đây?
| $(SPC)$ | |
| $(SCD)$ | |
| $(SBC)$ | |
| $(SBP)$ |
Trong $(\alpha)$, cho tứ giác $ABCD$ có $AB$ cắt $CD$ tại $E$, $AC$ cắt $BD$ tại $F$, $S$ là điểm không thuộc $(\alpha)$. Giao tuyến của $(SAB)$ và $(SCD)$ là
| $AC$ | |
| $SD$ | |
| $CD$ | |
| $SE$ |
Cho tam giác $ABC$. Có thể xác định được bao nhiêu mặt phẳng chứa tất cả các đỉnh của tam giác $ABC$?
| $1$ | |
| $3$ | |
| $4$ | |
| $2$ |
Trong không gian cho $4$ điểm không đồng phẳng. Có thể xác định được bao nhiêu mặt phẳng phân biệt từ các điểm đã cho?
| $6$ | |
| $3$ | |
| $4$ | |
| $2$ |
Kí hiệu nào sau đây là tên của mặt phẳng?
| $(P)$ | |
| $Q$ | |
| $AB$ | |
| $a$ |
