Trong không gian \(Oxyz\), cho điểm \(M(1;-3;4)\), đường thẳng \(d\colon\dfrac{x+3}{3}=\dfrac{y-5}{-5}=\dfrac{z-2}{-1}\) và mặt phẳng \((P)\colon2x+z-2=0\). Viết phương trình đường thẳng \(\Delta\) đi qua \(M\), vuông góc với \(d\) và song song với \((P)\).
| \(\Delta\colon\dfrac{x-1}{1}=\dfrac{y+3}{-1}=\dfrac{z-4}{-2}\) | |
| \(\Delta\colon\dfrac{x-1}{-1}=\dfrac{y+3}{-1}=\dfrac{z-4}{-2}\) | |
| \(\Delta\colon\dfrac{x-1}{1}=\dfrac{y+3}{1}=\dfrac{z-4}{-2}\) | |
| \(\Delta\colon\dfrac{x-1}{1}=\dfrac{y+3}{-1}=\dfrac{z-4}{2}\) |
Trong không gian \(Oxyz\), cho điểm \(A(3;5;3)\) và hai mặt phẳng \((P)\colon2x+y+2z-8=0\), \((Q)\colon x-4y+z-4=0\). Viết phương trình đường thẳng \(d\) đi qua \(A\) và song song với cả hai mặt phẳng \((P)\), \((Q)\).
| \(d\colon\begin{cases}x=3+t\\ y=5-t\\ z=3\end{cases}\) | |
| \(d\colon\begin{cases}x=3+t\\ y=5\\ z=3-t\end{cases}\) | |
| \(d\colon\begin{cases}x=3+t\\ y=5\\ z=3+t\end{cases}\) | |
| \(d\colon\begin{cases}x=3\\ y=5+t\\ z=3-t\end{cases}\) |
Trong không gian \(Oxyz\), cho đường thẳng \(d\colon\dfrac{x+1}{2}=\dfrac{y}{1}=\dfrac{z-2}{1}\), mặt phẳng \((P)\colon x+y-2z+5=0\) và điểm \(A(1;-1;2)\). Đường thẳng \(\Delta\) cắt \(d\) và \((P)\) lần lượt tại \(M\) và \(N\) sao cho \(A\) là trung điểm của \(MN\). Một vectơ chỉ phương của \(\Delta\) là
| \(\vec{u}=(2;3;2)\) | |
| \(\vec{u}=(1;-1;2)\) | |
| \(\vec{u}=(-3;5;1)\) | |
| \(\vec{u}=(4;5;-13)\) |
Trong không gian \(Oxyz\), gọi \(d'\) là hình chiếu vuông góc của đường thẳng \(d\colon\dfrac{x+1}{2}=\dfrac{y-2}{3}=\dfrac{z+3}{1}\) trên mặt phẳng tọa độ \((Oxy)\). Vectơ nào dưới đây là một vectơ chỉ phương của \(d'\)?
| \(\vec{u}=(2;3;0)\) | |
| \(\vec{u}=(2;3;1)\) | |
| \(\vec{u}=(-2;3;0)\) | |
| \(\vec{u}=(2;-3;0)\) |
Trong không gian \(Oxyz\), cho điểm \(M(1;-1;2)\) và hai đường thẳng \(d_1\colon\begin{cases}x=t\\ y=1-t\\ z=-1\end{cases}\), \(d_2\colon\dfrac{x+1}{2}=\dfrac{y-1}{1}=\dfrac{z+2}{1}\). Đường thẳng \(\Delta\) đi qua \(M\) và cắt cả hai đường thẳng \(d_1\), \(d_2\) có vectơ chỉ phương là \(\vec{u}=(1;a;b)\). Tính \(a+b\).
| \(a+b=1\) | |
| \(a+b=-1\) | |
| \(a+b=-2\) | |
| \(a+b=2\) |
Trong không gian \(Oxyz\), vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng \(d\colon\begin{cases}x=1+t\\ y=4\\ z=3-2t\end{cases}\)?
| \(\vec{u}=(1;4;3)\) | |
| \(\vec{u}=(1;4;-2)\) | |
| \(\vec{u}=(1;0;-2)\) | |
| \(\vec{u}=(1;0;2)\) |
Trong không gian \(Oxyz\), đường thẳng \(d\colon\dfrac{x-1}{2}=\dfrac{y-3}{-4}=\dfrac{z-7}{1}\) nhận vectơ nào dưới đây là một vectơ chỉ phương?
| \(\vec{a}=(-2;-4;1)\) | |
| \(\vec{b}=(2;4;1)\) | |
| \(\vec{c}=(1;-4;2)\) | |
| \(\vec{d}=(2;-4;1)\) |
Trên cánh đồng cỏ có hai con bò được cột vào hai cây cọc khác nhau. Biết khoảng cách giữa hai cọc là \(4\)m còn hai sợi dây cột hai con bò dài \(3\)m và \(2\)m. Tính phần diện tích mặt cỏ lớn nhất mà hai con bò có thể ăn chung (lấy giá trị gần đúng nhất).
| \(1,574\)m\(^2\) | |
| \(1,034\)m\(^2\) | |
| \(1,989\)m\(^2\) | |
| \(2,824\)m\(^2\) |
Gọi tam giác cong \(OAB\) là hình phẳng giới hạn bởi đồ thị các hàm số \(y=2x^2\), \(y=3-x\), \(y=0\) (như hình vẽ).
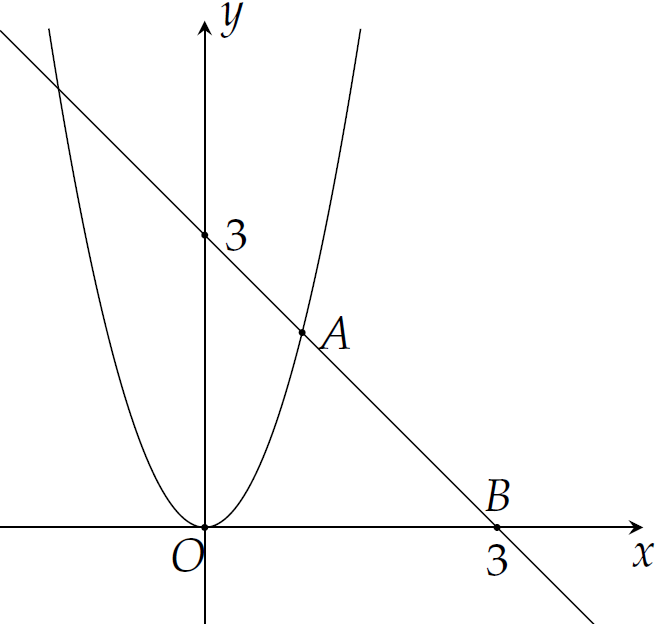
Tính diện tích \(S\) của tam giác cong \(OAB\).
| \(S=\dfrac{8}{3}\) | |
| \(S=\dfrac{4}{3}\) | |
| \(S=\dfrac{5}{3}\) | |
| \(S=\dfrac{10}{3}\) |
Tính diện tích hình phẳng giới hạn bởi các đường \(y=x^2\), \(y=\dfrac{x^2}{8}\), \(y=\dfrac{27}{x}\).
| \(\dfrac{63}{8}\) | |
| \(27\ln2-\dfrac{63}{8}\) | |
| \(27\ln2\) | |
| \(27\ln2-\dfrac{63}{4}\) |
Tính diện tích hình phẳng giới hạn bởi các đường \(y=x^2\), \(y=-\dfrac{1}{3}x+\dfrac{4}{3}\) và trục hoành như hình vẽ.
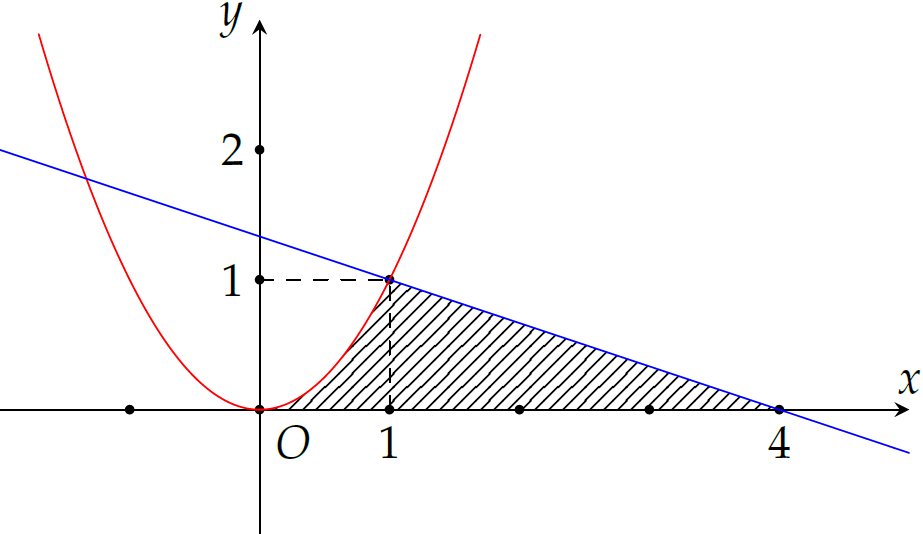
| \(\dfrac{7}{3}\) | |
| \(\dfrac{56}{3}\) | |
| \(\dfrac{39}{2}\) | |
| \(\dfrac{11}{6}\) |
Tính diện tích phần hình phẳng gạch chéo (tam giác cong \(OAB\)) trong hình vẽ.
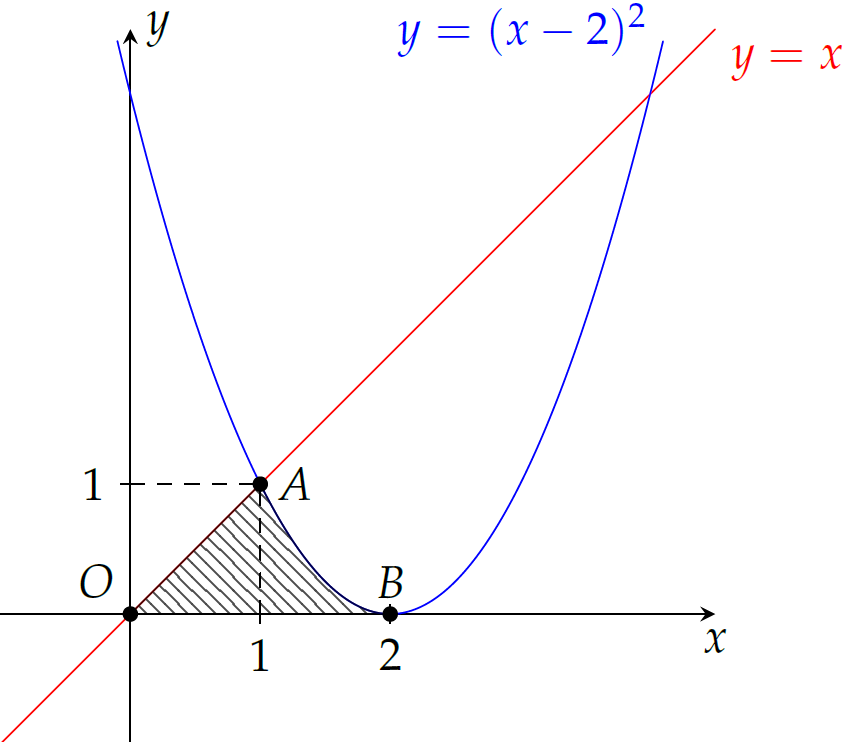
| \(\dfrac{5}{6}\) | |
| \(\dfrac{5\pi}{6}\) | |
| \(\dfrac{8}{15}\) | |
| \(\dfrac{8\pi}{15}\) |
Diện tích của hình phẳng giới hạn bởi các đường \(y=\sqrt{x}\), \(y=2-x\) và trục hoành bằng
| \(\dfrac{5}{6}\) | |
| \(\dfrac{5\pi}{6}\) | |
| \(\dfrac{7}{6}\) | |
| \(\dfrac{7\pi}{6}\) |
Tính diện tích \(S\) của hình phẳng (phần gạch sọc) trong hình.
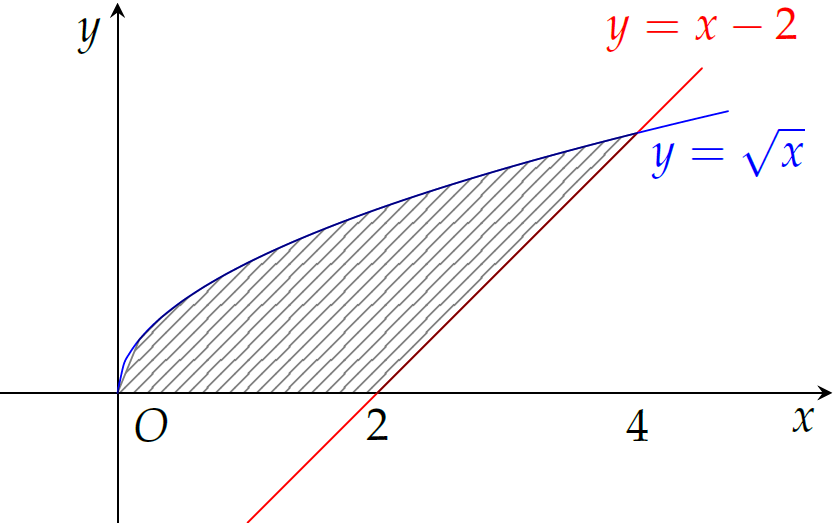
| \(S=\dfrac{8}{3}\) | |
| \(S=\dfrac{10}{3}\) | |
| \(S=\dfrac{11}{3}\) | |
| \(S=\dfrac{7}{3}\) |
Một tổ có \(6\) học sinh nam và \(4\) học sinh nữ. Chọn ngẫu nhiên \(4\) học sinh. Xác suất để trong \(4\) học sinh được chọn luôn có học sinh nữ là
| \(\dfrac{1}{14}\) | |
| \(\dfrac{1}{210}\) | |
| \(\dfrac{13}{14}\) | |
| \(\dfrac{209}{210}\) |
Từ một đội văn nghệ gồm \(5\) nam và \(8\) nữ, cần lập một nhóm gồm \(4\) người hát tốp ca. Xác suất để trong \(4\) người được chọn đều là nam bằng
| \(\dfrac{\mathrm{C}_8^4}{\mathrm{C}_{13}^4}\) | |
| \(\dfrac{\mathrm{C}_5^4}{\mathrm{C}_{13}^4}\) | |
| \(\dfrac{\mathrm{C}_8^4}{\mathrm{A}_{13}^4}\) | |
| \(\dfrac{\mathrm{A}_5^4}{\mathrm{C}_8^4}\) |
Trong một tổ có \(3\) học sinh nữ và \(7\) học sinh nam. Giáo viên chủ nhiệm chọn ngẫu nhiên \(3\) học sinh để lập nhóm tham gia trò chơi dân gian. Xác suất để \(3\) học sinh được chọn có cả nam và nữ là
| \(\dfrac{7}{20}\) | |
| \(\dfrac{7}{60}\) | |
| \(\dfrac{7}{10}\) | |
| \(\dfrac{7}{30}\) |
Một hộp có \(5\) viên bi xanh, \(6\) viên bi đỏ và \(7\) viên bi vàng. Chọn ngẫu nhiên \(5\) viên bi trong hộp. Tính xác suất để \(5\) viên bi được chọn có đủ \(3\) màu và số bi đỏ bằng với số bi vàng.
| \(\dfrac{95}{408}\) | |
| \(\dfrac{313}{408}\) | |
| \(\dfrac{5}{102}\) | |
| \(\dfrac{13}{408}\) |
Cho \(A=\{0;1;2;3;4;5;6;7\}\) và \(E=\left\{\overline{a_1a_2a_3a_4}\,|\,a_1,a_2,a_3,a_4\in A,\,a_1\neq0\right\}\). Lấy ngẫu nhiên một phần tử thuộc \(E\). Tính xác suất để phần tử đó là số chia hết cho \(5\).
| \(\dfrac{13}{49}\) | |
| \(\dfrac{5}{16}\) | |
| \(\dfrac{13}{48}\) | |
| \(\dfrac{1}{4}\) |
Gieo một con súc sắc cân đối và đồng chất. Xác suất để xuất hiện mặt có số chấm là một số nguyên tố bằng
| \(\dfrac{1}{4}\) | |
| \(\dfrac{1}{2}\) | |
| \(\dfrac{2}{3}\) | |
| \(\dfrac{1}{3}\) |
