Gọi \((H)\) là hình phẳng giới hạn bởi các đường \(y=3^x\), \(y=0\), \(x=0\) và \(x=3\). Thể tích \(V\) của khối tròn xoay tạo thành khi quay \((H)\) quanh trục \(Ox\) được xác định bởi công thức
| \(V=\pi\displaystyle\int\limits_{0}^{3}3^{x+1}\mathrm{\,d}x\) | |
| \(V=\displaystyle\int\limits_{0}^{3}3^{x+1}\mathrm{\,d}x\) | |
| \(V=\pi\displaystyle\int\limits_{0}^{3}9^x\mathrm{\,d}x\) | |
| \(V=\displaystyle\int\limits_{0}^{3}9^x\mathrm{\,d}x\) |
Cho hình phẳng \((H)\) giới hạn bởi các đường \(y=x^2+3\), \(y=0\), \(x=0\), \(x=2\). Gọi \(V\) là thể tích của khối tròn xoay được tạo thành khi quay \((H)\) xung quanh trục \(Ox\). Mệnh đề nào dưới đây đúng?
| \(V=\pi\displaystyle\int\limits_{0}^{2}\left(x^2+3\right)^2\mathrm{\,d}x\) | |
| \(V=\pi\displaystyle\int\limits_{0}^{2}\left(x^2+3\right)\mathrm{\,d}x\) | |
| \(V=\displaystyle\int\limits_{0}^{2}\left(x^2+3\right)^2\mathrm{\,d}x\) | |
| \(V=\displaystyle\int\limits_{0}^{2}\left(x^2+3\right)\mathrm{\,d}x\) |
Cho hàm số \(y=\pi^x\) có đồ thị \((C)\). Gọi \(D\) là hình phẳng giới hạn bởi \((C)\), trục hoành và hai đường thẳng \(x=2\), \(x=3\). Thể tích của khối tròn xoay tạo thành khi quay \(D\) quanh trục hoành được tính bởi công thức
| \(V=\pi^2\displaystyle\int\limits_{2}^{3}\pi^x\mathrm{\,d}x\) | |
| \(V=\pi^3\displaystyle\int\limits_{2}^{3}\pi^x\mathrm{\,d}x\) | |
| \(V=\pi\displaystyle\int\limits_{2}^{3}\pi^{2x}\mathrm{\,d}x\) | |
| \(V=\pi\displaystyle\int\limits_{3}^{2}\pi^{2x}\mathrm{\,d}x\) |
Thể tích khối tròn xoay tạo thành do hình phẳng giới hạn bởi các đường \(y=\dfrac{x}{4}\), \(y=0\), \(x=1\), \(x=4\) quay quanh trục \(Ox\) là
| \(\dfrac{21\pi}{16}\) | |
| \(\dfrac{15}{16}\) | |
| \(\dfrac{21}{16}\) | |
| \(\dfrac{15\pi}{8}\) |
Thể tích khối tròn xoay có được khi quay quanh trục \(Ox\) hình phẳng giới hạn bởi các đường \(y=\sqrt{x}\), \(y=0\), \(x=0\), \(x=1\) bằng
| \(V=\dfrac{\pi}{2}\) | |
| \(V=\dfrac{2\pi}{3}\) | |
| \(V=\dfrac{2}{3}\) | |
| \(V=\dfrac{1}{2}\) |
Cho hình phẳng \((H)\) giới hạn bởi đồ thị hàm số \(y=-x^2+3x-2\), trục hoành và hai đường thẳng \(x=1\), \(x=2\). Quay \((H)\) xung quanh trục hoành được khối tròn xoay có thể tích là
| \(V=\displaystyle\int\limits_{1}^{2}\left|x^2-3x+2\right|\mathrm{\,d}x\) | |
| \(V=\displaystyle\int\limits_{1}^{2}\left|x^2-3x+2\right|^2\mathrm{\,d}x\) | |
| \(V=\pi\displaystyle\int\limits_{1}^{2}\left(x^2-3x+2\right)^2\mathrm{\,d}x\) | |
| \(V=\pi\displaystyle\int\limits_{1}^{2}\left|x^2-3x+2\right|\mathrm{\,d}x\) |
Viết công thức tính thể tích \(V\) của vật thể nằm giữa hai mặt phẳng \(x=0\) và \(x=\ln4\), bị cắt bởi một mặt phẳng vuông góc với trục hoành tại điểm có hoành độ \(x\in(0;\ln4)\), có thiết diện là một hình vuông cạnh \(\sqrt{x\mathrm{e}^x}\).
| \(V=\pi\displaystyle\int\limits_{0}^{\ln4}x\mathrm{e}^x\mathrm{\,d}x\) | |
| \(V=\displaystyle\int\limits_{0}^{\ln4}\sqrt{x\mathrm{e}^x}\mathrm{\,d}x\) | |
| \(V=\displaystyle\int\limits_{0}^{\ln4}x\mathrm{e}^x\mathrm{\,d}x\) | |
| \(V=\pi\displaystyle\int\limits_{0}^{\ln4}\left[x\mathrm{e}^x\right]^2\mathrm{\,d}x\) |
Cho hình phẳng trong hình vẽ bên (phần tô đậm) quay quanh trục hoành.
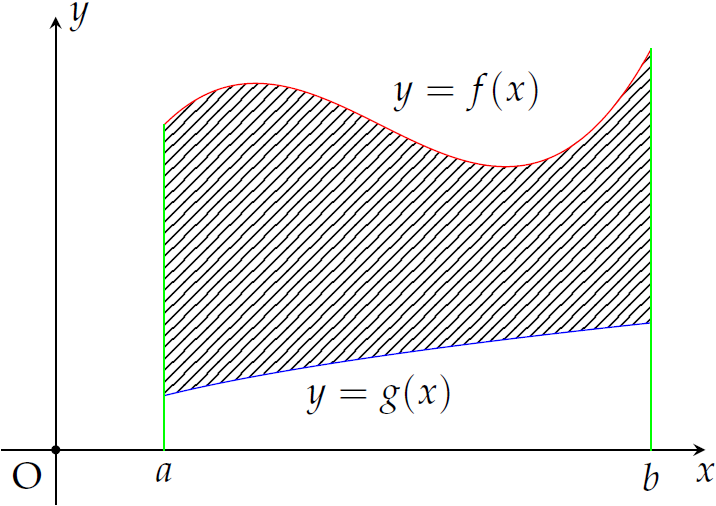
Thể tích khối tròn xoay tạo thành được tính theo công thức nào trong các công thức sau đây?
| \(V=\pi\displaystyle\int\limits_{a}^{b}\left[g^2(x)-f^2(x)\right]\mathrm{\,d}x\) | |
| \(V=\pi\displaystyle\int\limits_{a}^{b}\left[f(x)-g(x)\right]^2\mathrm{\,d}x\) | |
| \(V=\pi\displaystyle\int\limits_{a}^{b}\left[f(x)-g(x)\right]\mathrm{\,d}x\) | |
| \(V=\pi\displaystyle\int\limits_{a}^{b}\left[f^2(x)-g^2(x)\right]\mathrm{\,d}x\) |
Cho hàm số \(y=f(x)\) liên tục trên đoạn \([a;b]\). Gọi \(D\) là hình phẳng giới hạn bởi đồ thị của \(f(x)\), trục hoành và hai đường thẳng \(x=a\), \(x=b\). Thể tích của khối tròn xoay tạo thành khi quay \(D\) quanh trục hoành được tính theo công thức
| \(V=2\displaystyle\int\limits_{a}^{b}f^2(x)\mathrm{\,d}x\) | |
| \(V=2\pi^2\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x\) | |
| \(V=2\pi^2\displaystyle\int\limits_{a}^{b}f^2(x)\mathrm{\,d}x\) | |
| \(V=\pi\displaystyle\int\limits_{a}^{b}f^2(x)\mathrm{\,d}x\) |
Cho hàm số \(f(x)\) liên tục trên đoạn \([a;b]\). Gọi \((H)\) là hình phẳng giới hạn bởi đồ thị hàm số \(y=f(x)\), trục hoành và hai đường thẳng \(x=a\), \(x=b\); \(V\) là thể tích của khối tròn xoay được thành khi quay \((H)\) quanh trục \(Ox\). Khẳng định nào sau đây là đúng?
| \(V=\pi\displaystyle\int\limits_{a}^{b}\left|f(x)\right|\mathrm{\,d}x\) | |
| \(V=\displaystyle\int\limits_{a}^{b}f^2(x)\mathrm{\,d}x\) | |
| \(V=\pi\displaystyle\int\limits_{a}^{b}f^2(x)\mathrm{\,d}x\) | |
| \(V=\displaystyle\int\limits_{a}^{b}\left|f(x)\right|\mathrm{\,d}x\) |
Trong không gian \(Oxyz\), cho hai mặt phẳng \((\alpha)\colon x-y+nz-3=0\) và \((\beta)\colon2x+my+2z+6=0\). Với giá trị nào của \(m,\,n\) thì \((\alpha)\) và \((\beta)\) song song với nhau?
| \(m=-2,\;n=1\) | |
| \(m=1,\;n=-2\) | |
| \(m=-\dfrac{1}{2},\;n=1\) | |
| \(m=1,\;n=-\dfrac{1}{2}\) |
Trong không gian \(Oxyz\), cho hai mặt phẳng \((P)\colon x-3y+2z+1=0\) và \((Q)\colon(2m-1)x+m(1-2m)y+(2m-4)z+14=0\). Tìm \(m\) để \((P)\) và \((Q)\) vuông góc với nhau.
| \(m=1\) hoặc \(m=-\dfrac{3}{2}\) | |
| \(m=-1\) hoặc \(m=-\dfrac{3}{2}\) | |
| \(m=2\) | |
| \(m=\dfrac{3}{2}\) |
Trong không gian \(Oxyz\), cho điểm \(A(-1;2;1)\) và hai mặt phẳng \((P)\colon2x+4y-6z-5=0\), \((Q)\colon x+2y-3z=0\). Mệnh đề nào sau đây là đúng?
| Mặt phẳng \((Q)\) đi qua \(A\) và song song với \((P)\) | |
| Mặt phẳng \((Q)\) không đi qua \(A\) và song song với \((P)\) | |
| Mặt phẳng \((Q)\) đi qua \(A\) và không song song với \((P)\) | |
| Mặt phẳng \((Q)\) không đi qua \(A\) và không song song với \((P)\) |
Trong không gian \(Oxyz\), cho ba mặt phẳng \((\alpha)\colon x+y+2z+1=0\), \((\beta)\colon x+y-z+2=0\) và \((\gamma)\colon x-y+5=0\). Trong các mệnh đề sau, mệnh đề nào sai?
| \((\alpha)\bot(\beta)\) | |
| \((\gamma)\bot(\beta)\) | |
| \((\alpha)\parallel(\beta)\) | |
| \((\alpha)\bot(\gamma)\) |
Trong không gian \(Oxyz\), cặp mặt phẳng nào sau đây song song với nhau?
| \((P)\colon2x-y+z-5=0\) và \((Q)\colon-3x+2y-2z+10\) | |
| \((R)\colon x-y+z-3=0\) và \((S)\colon2x-2y+2z+6=0\) | |
| \((T)\colon x-y+z=0\) và \((U)\colon\dfrac{x}{2}-\dfrac{y}{2}+\dfrac{z}{2}=0\) | |
| \((X)\colon3x-y+2z-3=0\) và \((Y)\colon6z-2y-6=0\) |
Trong không gian \(Oxyz\), cho hai mặt phẳng \((P)\colon x+2y+2z-14=0\) và \((Q)\colon -x-2y-2z+16=0\). Vị trí tương đối của \((P)\) và \((Q)\) là
| Song song | |
| Trùng nhau | |
| Cắt nhau nhưng không vuông góc | |
| Vuông góc |
Trong không gian \(Oxyz\), cho hai mặt phẳng \((P)\colon2x-3y+4z+20=0\) và \((Q)\colon4x-13y-6z+40=0\). Vị trí tương đối của \((P)\) và \((Q)\) là
| Song song | |
| Trùng nhau | |
| Cắt nhau nhưng không vuông góc | |
| Vuông góc |
Trong không gian \(Oxyz\), cho hai mặt phẳng song song \((P)\) và \((Q)\) lần lượt có phương trình \(2x-y+z=0\) và \(2x-y+z-7=0\). Khoảng cách giữa hai mặt phẳng \((P)\) và \((Q)\) bằng
| \(7\) | |
| \(6\sqrt{7}\) | |
| \(7\sqrt{6}\) | |
| \(\dfrac{7}{\sqrt{6}}\) |
Trong không gian \(Oxyz\), cho mặt cầu \((S)\colon x^2+y^2+z^2-2y-2z-1=0\) và mặt phẳng \((P)\colon2x+2y-2z+15=0\). Tính khoảng cách ngắn nhất giữa điểm \(M\in(S)\) và điểm \(N\in(P)\).
| \(\dfrac{3\sqrt{3}}{2}\) | |
| \(\dfrac{3\sqrt{2}}{3}\) | |
| \(\dfrac{3}{2}\) | |
| \(\dfrac{2}{3}\) |
Trong không gian \(Oxyz\), cho mặt cầu \((S)\colon x^2+y^2+z^2-6x+4y-12=0\). Mặt phẳng nào sau đây cắt \((S)\) theo giao tuyến là một đường tròn có bán kính \(r=3\)?
| \((\alpha)\colon x+y+z+\sqrt{3}=0\) | |
| \((\beta)\colon2x+2y-z+12=0\) | |
| \((\gamma)\colon4x-3y-z-4\sqrt{26}=0\) | |
| \((\lambda)\colon3x-4y+5z-17+20\sqrt{2}=0\) |
