Cho hai số phức \(z_1=3+2i\) và \(z_2=1-5i\). Tìm phần thực và phần ảo của số phức \(z_1+z_2\).
| Phần thực là \(4\) và phần ảo là \(3\) | |
| Phần thực là \(4\) và phần ảo là \(-3i\) | |
| Phần thực là \(4\) và phần ảo là \(3i\) | |
| Phần thực là \(4\) và phần ảo là \(-3\) |
Cho số phức \(z=(2m-1)+(m^2-4)i\), \(m\in\mathbb{R}\). Tìm \(m\) để số phức \(z\) là số thuần ảo.
| \(m=2,\,m=-2\) | |
| \(m=2\) | |
| \(m=-\dfrac{1}{2}\) | |
| \(m=\dfrac{1}{2}\) |
Trên mặt phẳng tọa độ, tìm tọa độ của điểm \(M\) biểu diễn số phức \(z=5-i\).
| \(M(5;0)\) | |
| \(M(5;-1)\) | |
| \(M(0;-5)\) | |
| \(M(5;1)\) |
Tìm phần thực và phần ảo của số phức \(z=2-3i\).
| Phần thực là \(2\) và phần ảo là \(3\) | |
| Phần thực là \(2\) và phần ảo là \(-3\) | |
| Phần thực là \(2\) và phần ảo là \(3i\) | |
| Phần thực là \(2\) và phần ảo là \(-3i\) |
Cho hình phẳng \(D\) giới hạn bởi đồ thị hàm số \(y=2x^2+3x\), trục \(Ox\) và hai đường thẳng \(x=0,\,x=1\). Tính thể tích \(V\) của khối tròn xoay được tạo thành khi quay \(D\) quanh trục \(Ox\).
| \(V=\dfrac{13}{6}\) | |
| \(V=\dfrac{13\pi}{6}\) | |
| \(V=\dfrac{34\pi}{5}\) | |
| \(V=\dfrac{34}{5}\) |
Cho hình phẳng \(H\) giới hạn bởi đồ thị hàm số \(y=f(x)\) liên tục trên đoạn \([a;b]\), trục \(Ox\) và hai đường thẳng \(x=a,\,x=b\). Thể tích \(V\) của khối tròn xoay được tạo thành khi quay \(H\) quanh trục \(Ox\) là
| \(V=\pi\displaystyle\int\limits_a^b f(x)\mathrm{\,d}x\) | |
| \(V=\displaystyle\int\limits_a^b|f(x)|\mathrm{\,d}x\) | |
| \(V=\pi\displaystyle\int\limits_a^b f^2(x)\mathrm{\,d}x\) | |
| \(V=\displaystyle\int\limits_a^b f^2(x)\mathrm{\,d}x\) |
Tính diện tích \(S\) của hình phẳng giới hạn bởi đồ thị hàm số \(y=x^2+x\) và đường thẳng \(y=-x+3\).
| \(S=-\dfrac{32}{3}\) | |
| \(S=\dfrac{16}{3}\) | |
| \(S=16\) | |
| \(S=\dfrac{32}{3}\) |
Tính diện tích \(S\) của hình phẳng giới hạn bởi đồ thị hàm số \(y=3^x\), trục \(Ox\) và hai đường thẳng \(x=-1\), \(x=2\).
| \(S=\dfrac{26}{3}\) | |
| \(S=12\) | |
| \(S=\dfrac{12}{\ln3}\) | |
| \(S=\dfrac{26}{3\ln3}\) |
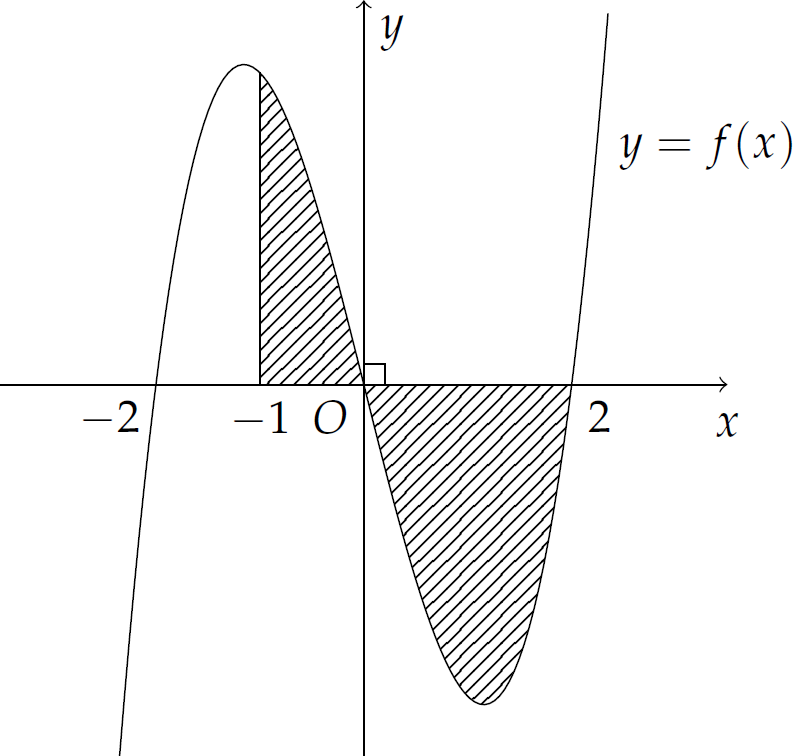
Cho hình phẳng \(H\) giới hạn bởi đồ thị hàm số \(y=f(x)\) trục \(Ox\) và đường thẳng \(x=-1\) (phần gạch sọc như hình trên). Gọi \(S\) là diện tích của hình phẳng \(H\). Mệnh đề nào dưới đây đúng?
| \(S=\displaystyle\int\limits_{-1}^0|f(x)|\mathrm{\,d}x-\displaystyle\int\limits_0^2|f(x)|\mathrm{\,d}x\) | |
| \(S=\displaystyle\int\limits_{-1}^2f(x)\mathrm{\,d}x\) | |
| \(S=\displaystyle\int\limits_{-1}^0f(x)\mathrm{\,d}x-\displaystyle\int\limits_0^2f(x)\mathrm{\,d}x\) | |
| \(S=\displaystyle\int\limits_{-1}^0f(x)\mathrm{\,d}x+\displaystyle\int\limits_0^2f(x)\mathrm{\,d}x\) |
Cho hình phẳng \(D\) giới hạn bởi đồ thị hai hàm số \(y=f(x),\,y=g(x)\) liên tục trên đoạn \([a;b]\) và hai đường thẳng \(x=a,\,x=b\). Diện tích \(S\) của hình phẳng \(D\) là
| \(S=\displaystyle\int\limits_a^b[f(x)+g(x)]\mathrm{\,d}x\) | |
| \(S=\displaystyle\int\limits_a^b |f(x)-g(x)|\mathrm{\,d}x\) | |
| \(S=\displaystyle\int\limits_a^b[f(x)-g(x)]\mathrm{\,d}x\) | |
| \(S=\displaystyle\int\limits_a^b[g(x)-f(x)]\mathrm{\,d}x\) |
Biết \(\displaystyle\int\limits_{\ln2}^{\ln5}(x+1)\mathrm{e}^x \mathrm{\,d}x=a\ln5+b\ln2\), với \(a,\,b\) là các số nguyên. Tính \(T=3a-2b\).
| \(T=19\) | |
| \(T=-4\) | |
| \(T=11\) | |
| \(T=-16\) |
Tính \(I=\displaystyle\int\limits_0^{\tfrac{\pi}{3}}\sin{2x}\mathrm{\,d}x\).
| \(I=-\dfrac{1}{4}\) | |
| \(I=0,019\) | |
| \(I=-\dfrac{3}{4}\) | |
| \(I=\dfrac{3}{4}\) |
Cho \(\displaystyle\int\limits_{-1}^5f(x)\mathrm{\,d}x=9\). Tính \(I=\displaystyle\int\limits_0^2f(3x-1)\mathrm{\,d}x\).
| \(I=26\) | |
| \(I=9\) | |
| \(I=3\) | |
| \(I=27\) |
Tính \(I=\displaystyle\int\limits_0^2(2x-x^3)\mathrm{\,d}x\).
| \(I=0\) | |
| \(I=10\) | |
| \(I=-4\) | |
| \(I=-10\) |
Cho \(\displaystyle\int\limits_{-1}^2f(x)\mathrm{\,d}x=5\) và \(\displaystyle\int\limits_0^2f(x)\mathrm{\,d}x=2\). Tính \(I=\displaystyle\int\limits_{-1}^0f(x)\mathrm{\,d}x\).
| \(I=7\) | |
| \(I=-3\) | |
| \(I=3\) | |
| \(I=1\) |
Cho \(\displaystyle\int\limits_a^b f(x)\mathrm{\,d}x=-3\) và \(\displaystyle\int\limits_a^b g(x)\mathrm{\,d}x=4\). Tính \(I=\displaystyle\int\limits_a^b [4f(x)-3g(x)]\mathrm{\,d}x\).
| \(I=25\) | |
| \(I=-24\) | |
| \(I=24\) | |
| \(I=0\) |
Cho hai hàm số \(f(x)\) và \(g(x)\) liên tục trên đoạn \([a;b]\). Mệnh đề nào dưới đây sai?
| \(\displaystyle\int\limits_a^b[f(x)-g(x)]\mathrm{\,d}x = \displaystyle\int\limits_a^b f(x)\mathrm{\,d}x - \displaystyle\int\limits_a^b g(x)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_a^b kf(x)\mathrm{\,d}x =k \displaystyle\int\limits_a^b f(x)\mathrm{\,d}x\) với \(k\) là hằng số | |
| \(\displaystyle\int\limits_a^b [f(x)\cdot {g(x)}]\mathrm{\,d}x=\displaystyle\int\limits_a^b f(x)\mathrm{\,d}x \cdot {\displaystyle\int\limits_a^b g(x)\mathrm{\,d}x}\) | |
| \(\displaystyle\int\limits_a^b [f(x)+g(x)]\mathrm{\,d}x = \displaystyle\int\limits_a^b f(x)\mathrm{\,d}x+\displaystyle\int\limits_a^b g(x)\mathrm{\,d}x\) |
Cho hàm số \(f(x)\) liên tục trên đoạn \([a;b]\) và \(a< c< b\). Mệnh đề nào dưới đây sai?
| \(\displaystyle\int\limits_a^b f(x)\mathrm{\,d}x+\displaystyle\int\limits_a^c f(x)\mathrm{\,d}x=\displaystyle\int\limits_b^c f(x)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_a^c f(x)\mathrm{\,d}x+\displaystyle\int\limits_c^b f(x)\mathrm{\,d}x=\displaystyle\int\limits_a^b f(x)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_a^b f(x)\mathrm{\,d}x=-\displaystyle\int\limits_b^a f(x)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_a^b f(x)\mathrm{\,d}x+\displaystyle\int\limits_b^a f(x)\mathrm{\,d}x=0\) |
Biết \(F(x)\) là một nguyên hàm của \(f(x)\) trên đoạn \([-2;3]\), \(\displaystyle\int\limits_{-2}^3f(x)\mathrm{\,d}x=12\) và \(F(3)=7\). Tính \(F(-2)\).
| \(F(-2)=19\) | |
| \(F(-2)=2\) | |
| \(F(-2)=5\) | |
| \(F(-2)=-5\) |
Cho hàm số \(f(x)\) liên tục trên đoạn \([a;b]\) và \(F(x)\) là một nguyên hàm của \(f(x)\) trên đoạn \([a;b]\). Mệnh đề nào dưới đây đúng?
| \(\displaystyle\int\limits_a^b f(x)\mathrm{\,d}x=F(a)-F(b)\) | |
| \(\displaystyle\int\limits_a^b f(x)\mathrm{\,d}x=f(b)-f(a)\) | |
| \(\displaystyle\int\limits_a^b f(x)\mathrm{\,d}x=f(a)-f(b)\) | |
| \(\displaystyle\int\limits_a^b f(x)\mathrm{\,d}x=F(b)-F(a)\) |
