Cho hai số phức $z_1=3-i$ và $z_2=-2+5i$. Khi đó mô-đun của số phức $z=z_1+z_2$ bằng
| $\sqrt{17}$ | |
| $2\sqrt{17}$ | |
| $\sqrt{39}$ | |
| $\sqrt{10}$ |
Với $a$ là số thực dương bất kỳ, $\ln(2023a)-\ln(2022a)$ bằng
| $\dfrac{2023}{2022}$ | |
| $\ln\dfrac{2023}{2022}$ | |
| $\dfrac{\ln2023}{\ln2022}$ | |
| $\ln a$ |
Có $30$ chiếc thẻ được đánh số thứ tự từ $1$ đến $30$. Chọn ngẫu nhiên một chiếc thẻ. Tính xác suất để chiếc thẻ được chọn mang số chia hết cho $3$.
| $\dfrac{2}{3}$ | |
| $\dfrac{3}{10}$ | |
| $\dfrac{1}{3}$ | |
| $\dfrac{1}{2}$ |
Giá trị nhỏ nhất của hàm số $y=x^3-3x^2$ trên đoạn $[1;5]$ bằng
| $50$ | |
| $-4$ | |
| $-45$ | |
| $-2$ |
Diện tích hình phẳng giới hạn bởi đồ thị của hàm số $y=x^5$, trục hoành và hai đường thẳng $x=-1$, $x=1$ bằng
| $\dfrac{3}{2}$ | |
| $\dfrac{1}{3}$ | |
| $7$ | |
| $5$ |
Tiệm cận đứng của đồ thị hàm số $y=\dfrac{2x-1}{x+1}$ là đường thẳng có phương trình
| $y=-1$ | |
| $x=-1$ | |
| $y=2$ | |
| $x=2$ |
Đồ thị hàm số $y=\dfrac{x-4}{2x+2}$ cắt trục tung tại điểm có tung độ bằng
| $\dfrac{1}{2}$ | |
| $-1$ | |
| $-2$ | |
| $4$ |
Hình lăng trụ $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông tại $A$, $AB=a$, $AC=2a$. Hình chiếu vuông góc của $A'$ lên mặt phẳng $(ABC)$ là điểm $I$ thuộc cạnh $BC$. Khoảng cách từ $A$ tới mặt phẳng $(A'BC)$ bằng
| $\dfrac{2}{5}a$ | |
| $\dfrac{\sqrt{3}}{2}a$ | |
| $\dfrac{2a\sqrt{5}}{5}$ | |
| $\dfrac{a\sqrt{5}}{5}$ |
Thể tích của khối nón có chiều cao $h$ và bán kính $r$ là
| $\dfrac{4}{3}\pi r^2h$ | |
| $2\pi r^2h$ | |
| $\pi r^2h$ | |
| $\dfrac{1}{3}\pi r^2h$ |
Cho $\displaystyle\displaystyle\int\sin x\mathrm{\,d}x=F(x)+C$. Khẳng định nào dưới đây đúng?
| $F'(x)=-\sin x$ | |
| $F'(x)=\sin x$ | |
| $F'(x)=-\cos x$ | |
| $F'(x)=\cos x$ |
Một hình trụ có bán kính đáy bằng $a$, chu vi thiết diện qua trục bằng $10a$. Chiều cao của khối trụ đã cho bằng
| $3a$ | |
| $a$ | |
| $4a$ | |
| $9a$ |
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ?
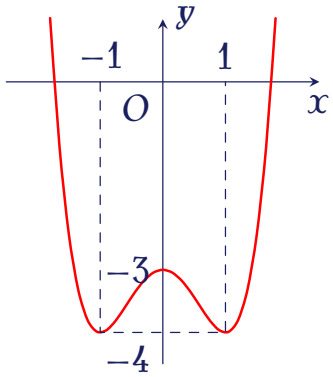
| $y=-x^4+2x^2-3$ | |
| $y=-x^3+3x$ | |
| $y=x^4-2x^2-3$ | |
| $y=x^3-3x-3$ |
Tập xác định của hàm số $y=\ln(2-x)$ là
| $\mathscr{D}=\mathbb{R}$ | |
| $\mathscr{D}=(-\infty;2)$ | |
| $\mathscr{D}=(2;+\infty)$ | |
| $\mathscr{D}=\mathbb{R}\setminus\{2\}$ |
Tập nghiệm bất phương trình $2^{x^2-3x}< 16$ là
| $(4;+\infty)$ | |
| $(-\infty;-1)\cup(4;+\infty)$ | |
| $(-1;4)$ | |
| $(-\infty;-1)$ |
Cho hình chóp $S.ABC$ có $SA$ vuông góc với mặt phẳng $(ABC)$, $SA=2a$, tam giác $ABC$ vuông tại $B$, $AB=a\sqrt{3}$ và $BC=a$. Góc giữa đường thẳng $SC$ và mặt phẳng $(ABC)$ bằng
| $90^{\circ}$ | |
| $30^{\circ}$ | |
| $45^{\circ}$ | |
| $60^{\circ}$ |
Cho khối chóp có diện tích đáy $B=2a^2$ và chiều cao $h=9a$. Thể tích của khối chóp đã cho bằng
| $9a^3$ | |
| $6a^3$ | |
| $3a^3$ | |
| $18a^3$ |
Trong không gian $Oxyz$, cho mặt phẳng $(P)\colon2x+y-z+3=0$. Vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng $(P)$?
| $\overrightarrow{n_1}=(2;1;-1)$ | |
| $\overrightarrow{n_3}=(1;-1;3)$ | |
| $\overrightarrow{n_4}=(2;-1;3)$ | |
| $\overrightarrow{n_2}=(2;1;3)$ |
Trong không gian $Oxyz$, gọi $\alpha$ là góc giữa hai mặt phẳng $(P)\colon x-\sqrt{3}y+2z+1=0$ và mặt phẳng $(Oxy)$. Khẳng định nào sau đây đúng?
| $\alpha=45^{\circ}$ | |
| $\alpha=30^{\circ}$ | |
| $\alpha=60^{\circ}$ | |
| $\alpha=90^{\circ}$ |
Trong không gian $Oxyz$, cho điểm $M(2;-1;3)$ và mặt phẳng $(P)\colon3x-2y+z+1=0$. Phương trình mặt phẳng đi qua $M$ và song song với $(P)$ là
| $3x-2y+z-11=0$ | |
| $2x-y+3z-14=0$ | |
| $3x-2y+z+11=0$ | |
| $2x-y+3z+14=0$ |
Nghiệm của phương trình $2^{2x-1}=8$ là
| $x=\dfrac{5}{2}$ | |
| $x=3$ | |
| $x=2$ | |
| $x=\dfrac{3}{2}$ |
