Gieo một con súc sắc cân đối và đồng chất. Cặp biến cố nào sau đây không đối nhau?

	\(A=\{1\}\) và \(B=\{2;3;4;5;6\}\)
	\(C=\{1;4;5\}\) và \(D=\{2;3;6\}\)
	\(E=\{1;4;6\}\) và \(F=\{2;3\}\)
	\(\Omega\) và \(\emptyset\)

Gieo đồng thời một đồng xu và một con súc sắc (cân đối và đồng chất), không gian mẫu có bao nhiêu phần tử?

	\(2\)
	\(6\)
	\(8\)
	\(12\)

Gieo một đồng xu cân đối và đồng chất \(2\) lần, không gian mẫu có bao nhiêu phần tử?

	\(2\)
	\(4\)
	\(6\)
	\(8\)

Gieo một con súc sắc cân đối và đồng chất, không gian mẫu có bao nhiêu phần tử?

	\(2\)
	\(6\)
	\(12\)
	\(18\)

Hai biến cố \(A\) và \(B\) xung khắc nhau nếu

	\(A\cap B=\emptyset\)
	\(A\cup B=\Omega\)
	\(P(B)=1-P(A)\)
	\(A\cap B=\emptyset\) và \(A\cup B=\Omega\)

Biến cố \(B\) là biến cố đối của biến cố \(A\) nếu

	\(A\cap B=\emptyset\)
	\(A\cup B=\Omega\)
	\(P(B)=1-P(A)\)
	\(A\cap B=\emptyset\) và \(A\cup B=\Omega\)

Gọi $A$ là biến cố của một phép thử. Phát biểu nào sau đây không đúng?

	\(nA>n\Omega\)
	\(A\subset\Omega\)
	\(0\leq P(A)\leq1\)
	\(P\left(\overline{A}\right)=1-P(A)\)

Phép thử nào sau đây không phải phép thử ngẫu nhiên?

	Gieo một con súc sắc cân đối và đồng chất
	Gieo một đồng xu cân đối và đồng chất
	Dùng phép toán \(\textbf{RanInt\#}\)(1,3) để xem kết quả
	Giải một phương trình bậc hai để xem nghiệm

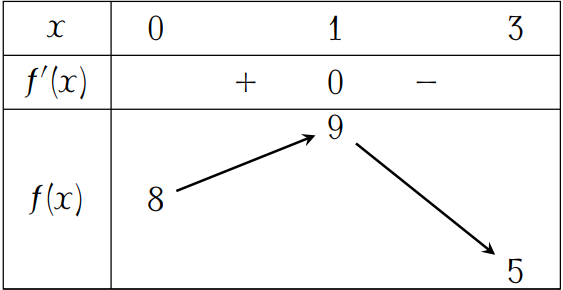
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình. Gọi \(S\) là tập hợp các số nguyên dương \(m\) để bất phương trình $$f(x)\geq mx^2\left(x^2-2\right)+2m$$có nghiệm thuộc đoạn \([0;3]\). Số phần tử của tập \(S\) là

	\(9\)
	\(10\)
	Vô số
	\(0\)

Có bao nhiêu giá trị nguyên của tham số \(m\) thuộc khoảng \((-6;5)\) sao cho phương trình $$2\cos2x+4\sin x-m\sqrt{2}=0$$vô nghiệm?

	\(3\)
	\(2\)
	\(4\)
	\(5\)

Một khu rừng có trữ lượng gỗ \(4\cdot10^5\text{m}^3\). Biết tốc độ sinh trưởng của các cây ở khu rừng đó là \(4\%\) mỗi năm. Hỏi sau \(5\) năm, khu rừng đó sẽ có khoảng bao nhiêu m\(^3\) gỗ?

	\(35\cdot10^5\text{m}^3\)
	\(4,8666\cdot10^5\text{m}^3\)
	\(2016\cdot10^3\text{m}^3\)
	\(125\cdot10^7\text{m}^3\)

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), \(SA=a\) và \(SA\) vuông góc với đáy. Gọi \(M\) là trung điểm của \(SB\), \(N\) thuộc cạnh \(SD\) sao cho \(SN=2ND\). Tính thể tích \(V\) của khối tứ diện \(ACMN\).

	\(V=\dfrac{1}{12}a^3\)
	\(V=\dfrac{1}{36}a^3\)
	\(V=\dfrac{1}{8}a^3\)
	\(V=\dfrac{1}{6}a^3\)

Anh X muốn mua một chiếc xe máy Yamaha Exciter 150i giá \(47.500.000\) đồng của cửa hàng Phú Tài nhưng vì chưa đủ tiền nên anh X đã quyết định mua theo hình thức như sau: trả trước \(25\) triệu đồng và trả góp trong \(12\) tháng, với lãi suất \(0,6\%\)/tháng. Hỏi mỗi tháng, anh X sẽ phải trả cho cửa hàng Phú Tài số tiền là bao nhiêu? (quy tròn đến hàng đơn vị).

	\(2.014.546\) đồng
	\(1.948.000\) đồng
	\(2.014.545\) đồng
	\(1.948.927\) đồng

Tìm \(m\) để bất phương trình \(x+\dfrac{4}{x-1}\geq m\) có nghiệm trên khoảng \((-\infty;1)\).

	\(m\leq3\)
	\(m\leq-3\)
	\(m\leq5\)
	\(m\leq-1\)

Đặt \(a=\log_23\), \(b=\log_53\). Nếu biểu diễn \(\log_645=\dfrac{a(m+nb)}{b(a+p)}\) với \(m,\,n,\,p\in\mathbb{N}\) thì \(m+n+p\) bằng

	\(3\)
	\(4\)
	\(6\)
	\(-3\)

Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(B\). Biết \(AC=a\), \(BC=\dfrac{a}{2}\), \(SA=\dfrac{a\sqrt{3}}{2}\) và cạnh \(SA\) vuông góc với mặt phẳng đáy. Khoảng cách từ \(A\) đến mặt phẳng \((SBC)\) bằng

	\(\dfrac{a\sqrt{6}}{4}\)
	\(a\sqrt{6}\)
	\(\dfrac{a\sqrt{3}}{2}\)
	\(\dfrac{a\sqrt{6}}{2}\)

Hình tạo bởi \(6\) đỉnh là \(6\) trung điểm của các cạnh của một tứ diện đều có bao nhiêu mặt phẳng đối xứng?

	\(3\)
	\(4\)
	\(9\)
	\(6\)

Phương trình \(2^{x-2}=3^{x^2+2x-8}\) có một nghiệm dạng \(x=\log_ab-4\) với \(a,\,b\) là các số nguyên dương thuộc khoảng \((1;5)\). Khi đó, \(a+2b\) bằng

	\(6\)
	\(9\)
	\(14\)
	\(7\)

Tiếp tuyến của đường cong \(\left(\mathscr{C}\right)\colon y=\dfrac{2x+1}{x-1}\) tại điểm \(M(2;5)\) cắt các trục tọa độ \(Ox\), \(Oy\) lần lượt tại \(A\) và \(B\). Tính diện tích tam giác \(OAB\).

	\(\dfrac{121}{6}\)
	\(\dfrac{121}{3}\)
	\(-\dfrac{121}{6}\)
	\(-\dfrac{121}{3}\)

Biết hàm số \(f(x)=\dfrac{a}{b^2\cdot3^x}\) có đồ thị đối xứng với đồ thị hàm số \(y=3^x\) qua đường thẳng \(x=-1\). Biết \(a,\,b\) là các số nguyên.

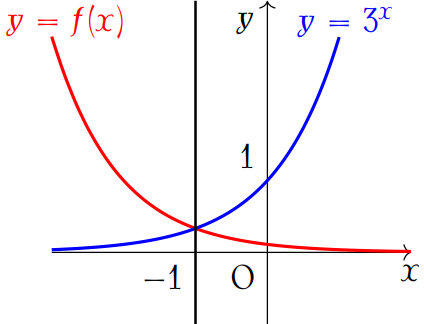
Chọn khẳng định đúng trong các khẳng định sau:

	\(b^2=9a\)
	\(b^2=4a\)
	\(b^2=6a\)
	\(b^2=a\)