Trong các mệnh đề sau, mệnh đề nào là đúng?
| Số cạnh của một hình đa diện luôn lớn hơn $7$ | |
| Số cạnh của một hình đa diện luôn lớn hơn hoặc bằng $8$ | |
| Số cạnh của một hình đa diện luôn lớn hơn $6$ | |
| Số cạnh của một hình đa diện luôn lớn hơn hoặc bằng $6$ |
Mỗi đỉnh của hình đa diện là điểm chung của ít nhất bao nhiêu cạnh?
| $5$ | |
| $4$ | |
| $3$ | |
| $2$ |
Mỗi đỉnh của một hình lập phương là đỉnh chung của đúng bao nhiêu mặt?
| $3$ | |
| $4$ | |
| $2$ | |
| $5$ |
Hãy chọn từ/cụm từ thích hợp để điền vào chỗ trống trong phát biểu: "Số cạnh của một hình đa diện luôn ............... số mặt của hình đa diện ấy".
| bằng | |
| nhỏ hơn hoặc bằng | |
| nhỏ hơn | |
| lớn hơn |
Mỗi cạnh của một khối đa diện là cạnh chung của bao nhiêu mặt của khối đa diện?
| Bốn mặt | |
| Hai mặt | |
| Ba mặt | |
| Năm mặt |
Cho hình chóp đều \(S.ABCD\) có cạnh đáy bằng \(a\), cạnh bên bằng \(2a\) và \(O\) là tâm của đáy. Gọi \(M\), \(N\), \(P\), \(Q\) lần lượt là các điểm đối xứng với \(O\) qua trọng tâm của các tam giác \(SAB\), \(SBC\), \(SCD\), \(SDA\) và \(S'\) là điểm đối xứng với \(S\) qua \(O\). Thể tích của khối chóp \(S'.MNPQ\) bằng
| \(\dfrac{20\sqrt{14}{a^3}}{81}\) | |
| \(\dfrac{40\sqrt{14}{a^3}}{81}\) | |
| \(\dfrac{10\sqrt{14}{a^3}}{81}\) | |
| \(\dfrac{2\sqrt{14}{a^3}}{9}\) |
Cho khối chóp có diện tích đáy \(B=6\) và chiều cao \(h=2\). Thể tích của khối chóp đã cho bằng
| \(6\) | |
| \(3\) | |
| \(4\) | |
| \(12\) |
Cho khối hộp chữ nhật có ba kích thước \(3,\,4,\,5\). Thể tích của khối hộp đã cho bằng
| \(10\) | |
| \(20\) | |
| \(12\) | |
| \(60\) |
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), \(SA=a\) và \(SA\) vuông góc với đáy. Gọi \(M\) là trung điểm của \(SB\), \(N\) thuộc cạnh \(SD\) sao cho \(SN=2ND\). Tính thể tích \(V\) của khối tứ diện \(ACMN\).
| \(V=\dfrac{1}{12}a^3\) | |
| \(V=\dfrac{1}{36}a^3\) | |
| \(V=\dfrac{1}{8}a^3\) | |
| \(V=\dfrac{1}{6}a^3\) |
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(B\). Biết \(AC=a\), \(BC=\dfrac{a}{2}\), \(SA=\dfrac{a\sqrt{3}}{2}\) và cạnh \(SA\) vuông góc với mặt phẳng đáy. Khoảng cách từ \(A\) đến mặt phẳng \((SBC)\) bằng
| \(\dfrac{a\sqrt{6}}{4}\) | |
| \(a\sqrt{6}\) | |
| \(\dfrac{a\sqrt{3}}{2}\) | |
| \(\dfrac{a\sqrt{6}}{2}\) |
Hình tạo bởi \(6\) đỉnh là \(6\) trung điểm của các cạnh của một tứ diện đều có bao nhiêu mặt phẳng đối xứng?
| \(3\) | |
| \(4\) | |
| \(9\) | |
| \(6\) |
Cho khối chóp \(S.ABC\) có thể tích bằng \(16\). Gọi \(M,\,N,\,P\) lần lượt là trung điểm của các cạnh \(SA\), \(SB\), \(SC\). Tính thể tích \(V\) của khối tứ diện \(AMNP\).
| \(V=12\) | |
| \(V=2\) | |
| \(V=14\) | |
| \(V=8\) |
Từ một tấm bìa hình vuông \(ABCD\) có cạnh bằng \(5\)dm, người ta cắt bỏ bốn tam giác bằng nhau \(AMB\), \(BNC\), \(CPD\), \(DQA\).
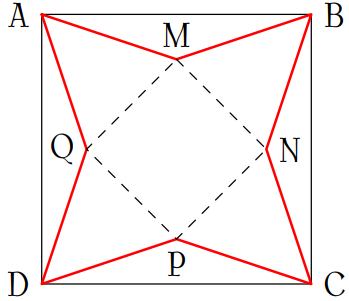
Với phần còn lại, người ta gắp lên và ghép lại để thành hình chóp tứ giác đều. Hỏi cạnh đáy của khối chóp bằng bao nhiêu để thể tích của nó là lớn nhất?
| \(\dfrac{3\sqrt{2}}{2}\) | |
| \(\dfrac{5}{2}\) | |
| \(\dfrac{5\sqrt{2}}{2}\) | |
| \(2\sqrt{2}\) |