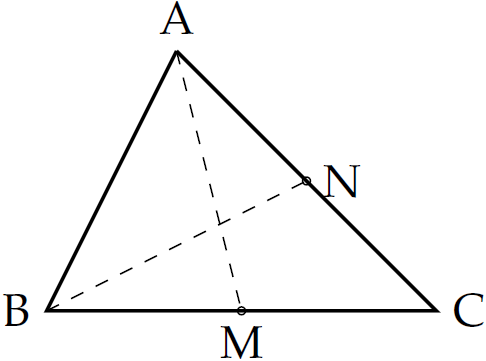
Bạn Thùy đặt một tấm bìa cứng hình tam giác (như hình vẽ) lên đầu một ngòi bút nhưng tấm bìa không bị rơi. Hỏi bạn Thùy đã đặt ngòi bút tại điểm nào của tấm bìa?
| Điểm \(A\) | |
| Trung điểm \(M\) | |
| Trung điểm \(N\) | |
| Giao điểm \(AM\) và \(BN\) |
Cho ba lực \(\overrightarrow{F_1}=\overrightarrow{MA}\), \(\overrightarrow{F_2}=\overrightarrow{MB}\) và \(\overrightarrow{F_3}=\overrightarrow{MC}\) cùng tác động vào một vật tại điểm \(M\) và vật đứng yên. Biết rằng \(\overrightarrow{F_1},\,\overrightarrow{F_2}\) đều có cường độ lực là \(60\)N, và chúng vuông góc với nhau. Tính cường độ lực \(\overrightarrow{F_3}\).
| \(84,58\)N | |
| \(84,86\)N | |
| \(84,85\)N | |
| \(120\)N |
Cho hai lực \(\overrightarrow{F_1}=\overrightarrow{MA}\) và \(\overrightarrow{F_2}=\overrightarrow{MB}\) cùng tác động vào một vật tại điểm \(M\). Cường độ hai lực \(\overrightarrow{F_1}\) và \(\overrightarrow{F_2}\) lần lượt là \(300\)N và \(400\)N, góc \(\widehat{AMB}=90^\circ\). Tính cường độ lực tổng hợp tác động vào vật.
| \(0\) | |
| \(700\) | |
| \(100\) | |
| \(500\) |
Cho hai lực \(\overrightarrow{F_1}\) và \(\overrightarrow{F_2}\) có cùng điểm đặt tại \(O\). Biết \(\overrightarrow{F_1}\) và \(\overrightarrow{F_2}\) đều có cường độ là \(100\)N, góc hợp bởi \(\overrightarrow{F_1}\) và \(\overrightarrow{F_2}\) là \(120^\circ\). Cường độ lực tổng hợp của chúng là
| \(200\)N | |
| \(50\sqrt{3}\)N | |
| \(100\sqrt{3}\)N | |
| \(100\)N |
Cho tam giác \(ABC\) đều, cạnh \(a\). Tính \(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|\).
| \(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=2a\) | |
| \(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=a\sqrt{3}\) | |
| \(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=\dfrac{\sqrt{3}}{2}\) | |
| \(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=a\) |
Cho tam giác \(ABC\) đều, cạnh \(a\). Tính \(\left|\overrightarrow{AB}+\overrightarrow{BC}\right|\).
| \(\left|\overrightarrow{AB}+\overrightarrow{BC}\right|=2a\) | |
| \(\left|\overrightarrow{AB}+\overrightarrow{BC}\right|=a\sqrt{3}\) | |
| \(\left|\overrightarrow{AB}+\overrightarrow{BC}\right|=\dfrac{\sqrt{3}}{2}\) | |
| \(\left|\overrightarrow{AB}+\overrightarrow{BC}\right|=a\) |
Cho tam giác \(ABC\) vuông cân tại \(C\) với \(AB=\sqrt{2}\). Tính \(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|\).
| \(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=\sqrt{5}\) | |
| \(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=2\sqrt{5}\) | |
| \(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=\sqrt{3}\) | |
| \(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=2\sqrt{3}\) |
Cho tam giác \(ABC\) vuông cân tại \(A\) với \(AB=a\). Tính \(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|\).
| \(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=a\sqrt{2}\) | |
| \(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=\dfrac{a\sqrt{2}}{2}\) | |
| \(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=2a\) | |
| \(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=a\) |
Cho tam giác \(ABC\) vuông tại \(A\) và có \(AB=3\), \(AC=4\). Tính \(\left|\overrightarrow{CA}+\overrightarrow{AB}\right|\).
| \(\left|\overrightarrow{CA}+\overrightarrow{AB}\right|=2\) | |
| \(\left|\overrightarrow{CA}+\overrightarrow{AB}\right|=2\sqrt{13}\) | |
| \(\left|\overrightarrow{CA}+\overrightarrow{AB}\right|=5\) | |
| \(\left|\overrightarrow{CA}+\overrightarrow{AB}\right|=\sqrt{13}\) |
Cho hình vuông \(ABCD\) cạnh \(a\), tâm \(O\). Tính \(\left|\overrightarrow{OB}+\overrightarrow{OC}\right|\).
| \(\left|\overrightarrow{OB}+\overrightarrow{OC}\right|=a\) | |
| \(\left|\overrightarrow{OB}+\overrightarrow{OC}\right|=a\sqrt{2}\) | |
| \(\left|\overrightarrow{OB}+\overrightarrow{OC}\right|=\dfrac{a}{2}\) | |
| \(\left|\overrightarrow{OB}+\overrightarrow{OC}\right|=\dfrac{a\sqrt{2}}{2}\) |
Cho hình vuông \(ABCD\) cạnh \(a\). Tính \(\left|\overrightarrow{AB}-\overrightarrow{DA}\right|\).
| \(\left|\overrightarrow{AB}-\overrightarrow{DA}\right|=0\) | |
| \(\left|\overrightarrow{AB}-\overrightarrow{DA}\right|=a\) | |
| \(\left|\overrightarrow{AB}-\overrightarrow{DA}\right|=a\sqrt{2}\) | |
| \(\left|\overrightarrow{AB}-\overrightarrow{DA}\right|=2a\) |
Cho tam giác \(ABC\) có \(M\) là điểm thỏa mãn \(\overrightarrow{MA}-\overrightarrow{MB}+\overrightarrow{MC}=\vec{0}\). Mệnh đề nào sau đây sai?
| \(MABC\) là hình bình hành | |
| \(\overrightarrow{AM}+\overrightarrow{AB}=\overrightarrow{AC}\) | |
| \(\overrightarrow{BA}+\overrightarrow{BC}=\overrightarrow{BM}\) | |
| \(\overrightarrow{MA}=\overrightarrow{BC}\) |
Cho tam giác \(ABC\) có $M$ là điểm thỏa mãn \(\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{AB}\). Xác định vị trí điểm \(M\).
| \(M\) là trung điểm cạnh \(AC\) | |
| \(M\) là trung điểm cạnh \(AB\) | |
| \(M\) là trung điểm cạnh \(BC\) | |
| \(M\) là điểm thứ tư của hình bình hành \(ABCM\) |
Cho tam giác \(ABC\) có \(M\) là điểm thỏa mãn \(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\vec{0}\). Xác định vị trí điểm \(M\).
| \(M\) là điểm thứ tư của hình bình hành \(ACBM\) | |
| \(M\) là trung điểm của đoạn thẳng \(AB\) | |
| \(M\equiv C\) | |
| \(M\) là trọng tâm tam giác \(ABC\) |
Cho tam giác \(ABC\) có \(D,\,E,\,F\) lần lượt là trung điểm các cạnh \(BC,\,CA,\,AB\). Hệ thức nào sau đây đúng?
| \(\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{BC}\) | |
| \(\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\overrightarrow{CA}+\overrightarrow{BC}+\overrightarrow{AC}\) | |
| \(\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\overrightarrow{AE}+\overrightarrow{BF}+\overrightarrow{CD}\) | |
| \(\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{AC}\) |
Cho hình bình hành \(ABCD\) tâm \(O\). Hãy tìm đẳng thức đúng.
| \(\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{AB}\) | |
| \(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}-\overrightarrow{OD}=\vec{0}\) | |
| \(\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{OC}-\overrightarrow{OD}\) | |
| \(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\vec{0}\) |
Cho bốn điểm phân biệt \(A,\,B,\,C,\,D\). Mệnh đề nào sau đây đúng?
| \(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{CB}\) | |
| \(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}=\overrightarrow{DA}\) | |
| \(\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{CD}+\overrightarrow{DA}\) | |
| \(\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{CD}+\overrightarrow{CB}\) |
Cho tam giác \(ABC\) có \(AB=AC\) và đường cao \(AH\). Đẳng thức nào sau đây đúng?
| \(\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AH}\) | |
| \(\overrightarrow{HA}+\overrightarrow{HB}+\overrightarrow{HC}=\vec{0}\) | |
| \(\overrightarrow{HB}+\overrightarrow{HC}=\vec{0}\) | |
| \(\overrightarrow{AB}=\overrightarrow{AC}\) |
Cho ba điểm phân biệt \(A,\,B,\,C\). Mệnh đề nào sau đây đúng?
| \(AB+BC=AC\) | |
| \(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}=\vec{0}\) | |
| \(\overrightarrow{AB}=\overrightarrow{BC}\Leftrightarrow\left|\overrightarrow{CA}\right|=\left|\overrightarrow{BC}\right|\) | |
| \(\overrightarrow{AB}-\overrightarrow{CA}=\overrightarrow{BC}\) |
Cho tam giác \(ABC\) với \(M\) là trung điểm cạnh \(BC\). Mệnh đề nào sau đây đúng?
| \(\overrightarrow{AM}+\overrightarrow{MB}+\overrightarrow{BA}=\vec{0}\) | |
| \(\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{AB}\) | |
| \(\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{MC}\) | |
| \(\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AM}\) |
