Hàm số nào dưới đây nghịch biến trên $\mathbb{R}$?
| $y=-x^3-x$ | |
| $y=-x^4-x^2$ | |
| $y=-x^3+x$ | |
| $y=\dfrac{x+2}{x-1}$ |
Trên đoạn $[1;5]$, hàm số $y=x+\dfrac{4}{x}$ đạt giá trị nhỏ nhất tại điểm
| $x=5$ | |
| $x=2$ | |
| $x=1$ | |
| $x=4$ |
Cho hàm số $y=ax^4+bx^2+c$ ($a,\,b,\,c\in\mathbb{R})$ có đồ thị là đường cong trong hình bên.
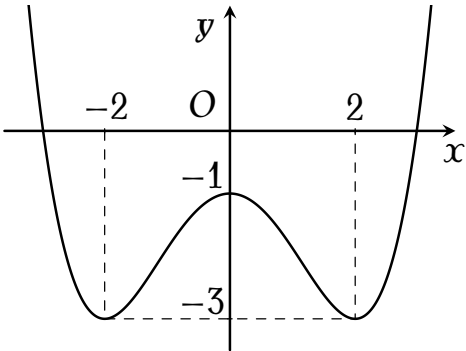
Giá trị cực đại của hàm số đã cho bằng
| $0$ | |
| $-1$ | |
| $-3$ | |
| $2$ |
Cho hàm số $f(x)=1+\sin x$. Khẳng định nào dưới đây đúng?
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=x-\cos x+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=x+\sin x+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=x+\cos x+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=\cos x+C$ |
Cho cấp số cộng $\left(u_n\right)$ với $u_1=7$ và công sai $d=4$. Giá trị của $u_2$ bằng
| $11$ | |
| $3$ | |
| $\dfrac{7}{4}$ | |
| $28$ |
Nếu $\displaystyle\displaystyle\int\limits_{2}^{5}f(x)\mathrm{\,d}x=2$ thì $\displaystyle\displaystyle\int\limits_{2}^{5}3f(x)\mathrm{\,d}x$ bằng
| $6$ | |
| $3$ | |
| $18$ | |
| $2$ |
Cho hình trụ có bán kính đáy $r$ và độ dài đường sinh $\ell$. Diện tích xung quanh $S_{xq}$ của hình trụ đã cho được tính theo công thức nào dưới đây?
| $S_{xq}=4\pi r\ell$ | |
| $S_{xq}=2\pi r\ell$ | |
| $S_{xq}=3\pi r\ell$ | |
| $S_{xq}=\pi r\ell$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
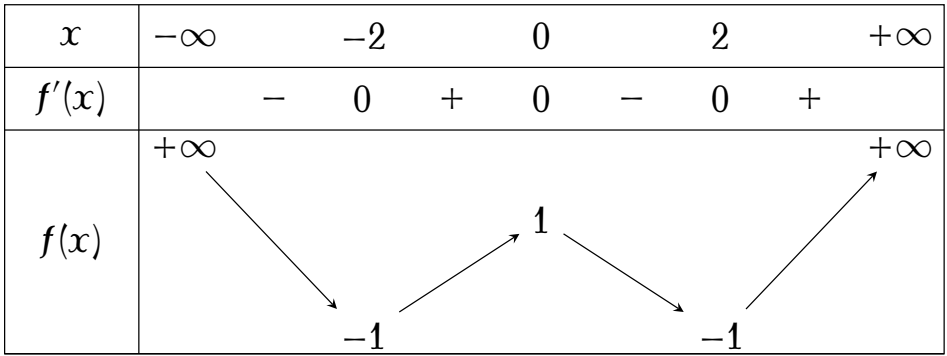
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
| $(0;+\infty)$ | |
| $(-\infty;-2)$ | |
| $(0;2)$ | |
| $(-2;0)$ |
Trên khoảng $(0;+\infty)$, đạo hàm của hàm số $y=\log_2x$ là
| $y'=\dfrac{1}{x\ln2}$ | |
| $y'=\dfrac{\ln2}{x}$ | |
| $y'=\dfrac{1}{x}$ | |
| $y'=\dfrac{1}{2x}$ |
Cho khối lăng trụ có diện tích đáy $B$ và chiều cao $h$. Thể tích $V$ của khối lăng trụ đã cho được tính theo công thức nào dưới đây?
| $V=\dfrac{1}{3}Bh$ | |
| $V=\dfrac{4}{3}Bh$ | |
| $V=6Bh$ | |
| $V=Bh$ |
Với $n$ là số nguyên dương, công thức nào dưới đây đúng?
| $P_n=n!$ | |
| $P_n=n-1$ | |
| $P_n=(n-1)!$ | |
| $P_n=n$ |
Trong không gian $Oxyz$, đường thẳng $d\colon\begin{cases}x=1+2t\\ y=2-2t\\ z=-3-3t\end{cases}$ đi qua điểm nào dưới đây?
| Điểm $Q(2;2;3)$ | |
| Điểm $N(2;-2;-3)$ | |
| Điểm $M(1;2;-3)$ | |
| Điểm $P(1;2;3)$ |
Hàm số nào dưới đây có đồ thị như đường cong trong hình bên?
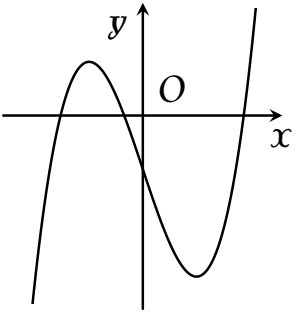
| $y=x^4-2x^2-1$ | |
| $y=\dfrac{x+1}{x-1}$ | |
| $y=x^3-3x-1$ | |
| $y=x^2+x-1$ |
Với mọi số thực $a$ dương, $\log_2\dfrac{a}{2}$ bằng
| $\dfrac{1}{2}\log_2a$ | |
| $\log_2a+1$ | |
| $\log_2a-1$ | |
| $\log_2a-2$ |
Tiệm cận đứng của đồ thị hàm số $y=\dfrac{3x+2}{x-2}$ là đường thẳng có phương trình
| $x=2$ | |
| $x=-1$ | |
| $x=3$ | |
| $x=-2$ |
Trên mặt phẳng tọa độ, cho $M(2;3)$ là điểm biểu diễn của số phức $z$. Phần thực của $z$ bằng
| $2$ | |
| $3$ | |
| $-3$ | |
| $-2$ |
Trong không gian $Oxyz$, cho hai vectơ $\overrightarrow{u}=(1;3;-2)$ và $\overrightarrow{v}=(2;1;-1)$. Tọa độ của vectơ $\overrightarrow{u}-\overrightarrow{v}$ là
| $(3;4;-3)$ | |
| $(-1;2;-3)$ | |
| $(-1;2;-1)$ | |
| $(1;-2;1)$ |
Trong không gian $Oxyz$, mặt phẳng $(P)\colon2x-3y+4z-1=0$ có một vectơ pháp tuyến là
| $\overrightarrow{n_4}=(-1;2;-3)$ | |
| $\overrightarrow{n_3}=(-3;4;-1)$ | |
| $\overrightarrow{n_2}=(2;-3;4)$ | |
| $\overrightarrow{n_1}=(2;3;4)$ |
Cho số phức $z=3-2i$, khi đó $2z$ bằng
| $6-2i$ | |
| $6-4i$ | |
| $3-4i$ | |
| $-6+4i$ |
Nếu $\displaystyle\displaystyle\int\limits_{2}^{5}f(x)\mathrm{\,d}x=3$ và $\displaystyle\displaystyle\int\limits_{2}^{5}g(x)\mathrm{\,d}x=-2$ thì $\displaystyle\displaystyle\int\limits_{2}^{5}[f(x)+g(x)]\mathrm{\,d}x$ bằng
| $5$ | |
| $-5$ | |
| $1$ | |
| $3$ |
